Mathématiques,
équation différentielle, fonction,
Bts groupe D 2017 .
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Un
réservoir d’une capacité de 10 litres contient 2 litres d’un concentré
de parfum. On y introduit à partir de l’instant initial t = 0, de
l’éthanol, avec un débit de 20 cm3 par seconde.
Le liquide présent dans le réservoir est mélangé en permanence par un
agitateur.
Dans tout le problème, Q(t ) désigne la quantité, en cm3,
d’éthanol présente dans le récipient
à l’instant t exprimé en secondes.
On rappelle qu’un litre vaut 1 000 cm3.
Partie A : Étude
qualitative du problème
1. a. Vérifier que
le réservoir contient 5 litres de mélange concentré-éthanol au bout de
150 s.
2 + 0,020 x150 = 5 L.
b. Au bout de
combien de temps le réservoir est-il plein ?
10 = 2 +0,020 t ; 8 = 0,02 t ; t = 8 / 0,02 = 400 s.
2. Alors que le
réservoir est plein, suite à un incident, la pompe continue à
l’alimenter dans les mêmes conditions. Un système de trop-plein a été
prévu dans ce cas de figure, et dès cet instant, chaque seconde 20 cm3
de liquide homogène s’échappe par ce système.
On s’intéresse à la quantité Q d’éthanol présente dans le récipient
depuis l’instant initial,moment où commence le remplissage du réservoir.
a. D’après vous,
comment varie cette quantité Q en fonction du temps ? Argumenter.
t < 400 s :
Q(t) exprimé en cm3, est proportionnelle au temps t exprimé
en seconde.
Q(t) = 20 t.
Q(t) croît linéairement au cours du temps
jusqu'à ce que le réservoir soit plein.
t
> 400 s :chaque seconde, 20 cm3 de mélange s'échappe du
réservoir tandis que 20 cm3 d'éthanol y entre. Q(t) croît
lentement.
b. Parmi les quatre
courbes ci-dessous (l’axe des abscisses représente le temps exprimé en
secondes, l’axe des ordonnées, la quantité Q exprimée en cm3),
une seule représente la quantité d’éthanol présente dans le réservoir
en fonction du temps. Laquelle ? Justifier votre choix.
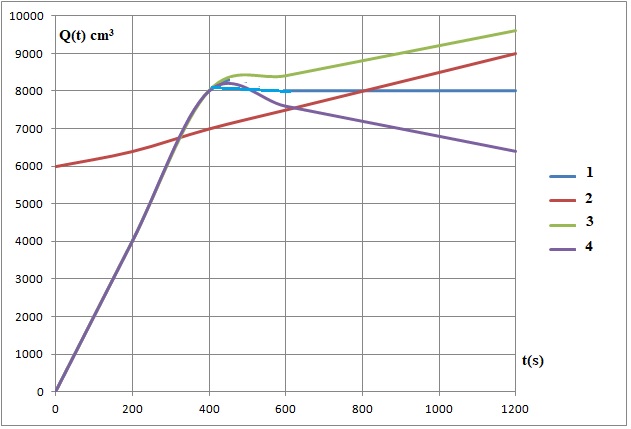
Courbe 3.
La quantité initiale d'éthanol est nulle ; Q(t) croît linéairement
jusqu'à t = 400 puis croît plus lentement.
|
....
.....
|
Partie B : Une équation
différentielle
On admet que, pour tout instant t > 400, la quantité d’éthanol
présente dans le réservoir vérifie l’équation différentielle :
Q′(t )+0,002Q(t ) = 20, avec Q(400) = 8000.
On considère l’équation différentielle suivante :
(E) : y′+0,002y = 20
où l’inconnue y est une fonction de la variable t , avec t appartenant
à [400 ; +∞[.
1. Déterminer
l’ensemble des solutions de l’équation différentielle homogène associée
(E0) : y′+0,002y = 0.
y = A exp(-0,002t),
avec A une constante.
2. Déterminer le
réel a tel que la fonction constante a soit une solution
particulière de (E).
0,002a = 20 ; a = 20 /0,002 = 10 000.
3. En déduire
l’ensemble des solutions de (E).
y = A exp(-0,002t) +10 000.
4. Déterminer la
fonction Q répondant au problème posé.
A t=400, Q(t) = 8 000.
8 000 =Aexp(-0,002 x400) + 10 000.
-2000 = A exp(-0,8) ; A = -2000 / exp(-0,8) ~ - 4451.
Q(t) = -4451 exp(-0,002t)
+10 000.
Partie C : Étude
d’une fonction
On considère la fonction Q1 définie pour tout réel t de
l’intervalle [400 ; +∞[ par :
Q1(t ) = 10000−4451,1exp(−0,002t) .
On admet que cette fonction exprime la quantité d’éthanol présente dans
le récipient pour t >400.
1. Calculer la
limite de Q1 en +∞. Interpréter ce résultat.
Quand t tend vers plus l'infini, exp(−0,002t) tend vers
zéro et Q1(t) tend vers 10 000.
Finalement le récipient contient 10 L d'éthanol.
2. En étudiant les variations de la
fonction Q1 vérifier mathématiquement le résultat de la
partie A question 2. a.
Q'1(t) = 4551,1 x 0,002 exp(-0,002t) ~8,90 exp(-0,002t).
Q'1(t) est positive et Q1(t) est strictement
croissante sur [400 ; +∞[ depuis
8000 jusqu'à 10 000.
3.
On veut déterminer l’instant t où la proportion d’éthanol dans le
réservoir vaut 85%. Par la méthode de votre choix déterminer une valeur
approchée à l’unité près de la solution.
10 000 *0,85 = 8500 ;
8500 = 10 000-4451,1 exp(-0,002t) ;
1500 = 4451,1 exp(-0,002t) ;
exp(-0,002t) = 1500 / 4451,1 ~0,337 ;
-0,002t = ln(0,337) = -1,0877 ;
t ~1,0877 / 0,002 ~ 544 s.
On donnera une description de la méthode utilisée.
|
|
|
4. Cette question fait l’objet d’un
QCM: on écrira l’unique réponse correcte sur la copie, aucune
justification n’est demandée.
On considère l’algorithme suivant :
Demander A un nombre réel compris strictement entre 8 000 et 12 000
Mettre 400 dans T
Tant que 10000−4451,1exp(−0,002T )< A
Mettre T +10 dans T
Fin du Tant que
Afficher T
Cet algorithme a pour but de :
Réponse a. : Déterminer la valeur exacte de l’équation Q1(t
)= A dans l’intervalle [400 ; +∞[.
Réponse b. :Déterminer une valeur approchée par défaut à 10 près de
l’équation Q1(t ) = A dans l’intervalle [400 ; +∞[.
Réponse c. : Déterminer une valeur approchée par excès à 10 près de
l’équation Q1(t ) = A dans l’intervalle [400 ; +∞[.
Réponse d. : Déterminer les solutions de l’inéquation Q1(t )
> A dans l’intervalle [400 ; +∞[
|
|
|
|
On
choisit A = 8200 :
T
|
400
|
410
|
420
|
430
|
440
|
450
|
460
|
Q1(t)
|
8000
|
~
8039,6
|
8078,4
|
8116,5
|
8153,8
|
8190
|
8226
|
| 10000−4451,1exp(−0,002T
)< A |
Vrai
|
Vrai
|
Vrai
|
Vrai
|
Vrai
|
Vrai
|
Faux.
|
Réponse c.
|
|