Ecran de
smartphone,
Bac S Antilles 09 / 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
Exercice 3. (5 points)
Lorsqu'il
est allumé, un écran de téléphone portable est constitué de pixels (
petits rectangles) de luminosité et de couleurs différentes et qui
constituent au final l'image affichée. Chaque pixel est constitué de 3
sous-pixels de couleurs respectives rouge, vertn bleu ( RVB).
Diffraction par un petit miroir.
Lorsqu'un
faisceau laser rencontre un objet réfléchissant comme un miroir
sufisamment petit, il se produit un phénomène analogue à celui observé
lorsque ce faisceau laser rencontre une fente très fine ou un fil très
fin : on observe sur un écran un phénomène de diffraction obtenue dans
ce cas par réflexion.
On note : a : largeur du miroir ; D distance écran - miroir ; l longueur d'onde de la lumière laser ; q demi-angle délimitant les premiers minima d'amplitude.
1.1. Citer deux propriétés du laser.
Faisceau très directif, lumière monochromatique ; forte puissance par unité de surface.
1.2 Donner en le
justifiant, un ordre de gandeur possible de la largeur a du miroir si
on utilise une lumière visible pour observer une figure de diffraction.
La largeur du miroir doit être de l'ordre de grandeur de la longueur d'onde ( environ 0,6 µm).
Les deux figures de diffraction ci-dessous ont été obtenues sur un
écran avec, pour l'une, un laser vert et, pour l'autre, un laser rouge
et dans les mêmes conditions expérimentales.

1.3 Rappeler la relation entre q, a et l. En déduire alors le laser utilisé pour chaque figure de diffraction.
q = l / a = ½L / D avec L : largeur de la tache centrale.
q est d'autant plus grand que la longueur d'onde est grande.
Or lrouge > lvert ; la figure 2 correspond au rouge.
1.4 Sachant que le laser rouge utilisé a une longueur d'onde égale à 632,8 nm, en déduire la longueur d'onde du laser vert.
L rouge = 2 lrouge D /a ; L vert = 2 lvert D /a ;
lvert = lrouge Lvert / Lrouge =
632,8 x1,5 / 2 ~ 474 nm.
|
|
...
|
|
Détermination de la taille d'un pixel.
L'écran est constitué d'un quadrillage de pixels très petits que l'on
peut considérer comme autant de carrés réfléchissants accolés.
On réalise le dispositif expérimental suivant et on observe la figure
obtenue sur l'écran quadrillé lorsqu'on envoie un faisceau laser sur
l'écran du smartphone.
D = (1,74 ±0,03) m ; l = 632,8 nm.
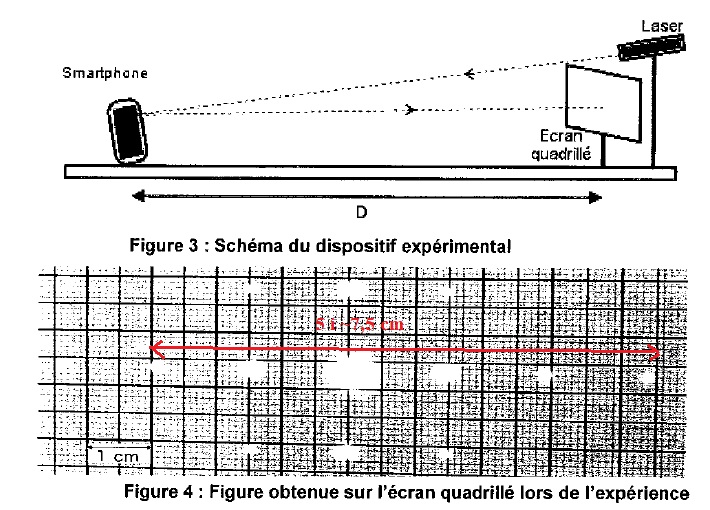
Cette figure permet de déterminer la largeur d'un pixel. En effet, on
peut relier la distance i entre deux points lumineux présents sur
l'écran quadrillé à la distance a séparant les centres de deux pixels
accolés de l'écran du smartphone par la relation i = lD / a..
2.1. Déterminer i.
i = 7,5 / 5 = 1,5 cm.
2.2. En déduire que a ~75 µm.
a = lD / i = 632,8 10-9x1,74 /(1,5 10-2)=7,34 10-5 m ~75 µm.
|
|
3. Vision de l'écran du smartphone.
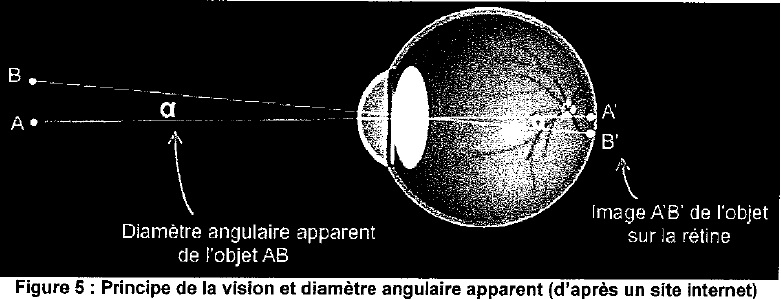
Pouvoir séparateur de l'oeil : amini = 3,0 10-4 rad.
Si le diamètre angulaire apparent de l'objet AB est inférieur au
pouvoir séparateur de l'oeil alors l'objet AB est vu comme un seul
point sur la rétine ( A' et B' sont confondus sur la rétine).
3.1. Sachant que le
point le plus proche qui peut être vu avec neteté ( appelé punctum
proximum ) se trouve à 25 cm d'un oeil normal, déterminer la
taille du plus petit objet AB visible.
AB = amini x 0,25 = 3,0 10-4 x 0,25 = 7,5 10-5 m = 75 µm.
3.2. Déterminer la
distance entre les centres de deux pixels successifs du smartphone
considéré sachant que l'on peut lire sur la notice technique
l'information suivante : " résolution 367 ppp "
ppp : pixel par pouce ; 1 pouce = 2,54 cm.
2,54 10-2 / 367 = 6,92 10-5 m = 69,2 µm.
3.3.
Montrer qu'il est impossible à l'oeil nu de distinguer deux pixels de
l'écran. Cette propriété est-elle interessante pour l'utilisation du
smartphone ?
La distance entre deux pixels successifs est inférieure à la taille du plus petit objet visible à l'oeil nu.
Sur la rétine on observe une image et non pas un ensemble de points.
4. Image numérique.
Chaque pixel de l'écran est codé sur trois octets ( 1 octet = 8 bits par couleur ).
4.1 Pourquoi parle t-on d'un codage 24 bits dans ce cas ?
Pour obtenir une image en couleur, il faut trois octets par pixels ( un pour le rouge, un pour le vert et un pour le bleu ) .
Trois octets correspondent à 3 x 8 = 24 bits.
4.2. Pourquoi parle -ton de 16 millions de couleurs possibles ? Calculer le nombre exact de couleurs.
L'oil perçoit toute couleur comme la combinaison de trois couleurs primaire rouge, bleu, vert.
En modulant la luminosité de chaque sous-pixel, on peut reproduire la couleur souhaitée.
224 = 1,68 107 = 16,8 millions.
4.3. On considère deux zones de l'écran, chacune de 9 pixels dont on donne les codages RVB.
L'une est colorée, l'autre en niveaux de gris. Peut-on les distinguer à l'aide du codage ci-dessous.

La zone située à gauche est colorée : pour chaque pixel, l'un des sous pixels n'a aucune luminosité.
La zone de droite est en niveau de gris : pour chaque pixel, les trois sous pixels ont la même luminosité.
|
|