A
propos des éclipses solaires, Bac S Inde 2018.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
.
|
|
Partie A. L'éclipse du 21 août 2017.
1. Rotation de la terre.
Dans
le référentiel géocentrique, la terre effectue un tour sur elle-même en
environ 23 h 56 min ( durée du jour sidéral). On se place dans ce
référentiel.
1.1. Quelle est la nature du mouvement d'un point situé sur l'équateur ?
Le mouvement d'un point situé sur l'équateur est circulaire uniforme.
1.2. Montrer que la vitesse d'un point situé sur l'équateur est égale à 465 m /s.
Circonférence de la terre à l'équateur :3,14 x 12742 x1000 = 4,003 107 m.
Durée : 23 x3600 +56 x60 = 8,616 104 s.
Vitesse : (4,003 107 / 8,616 104) ~465 m s-1.
1.3. Cette vitesse d'un point à la surface de la terre dépend de la latitude a selon : v = 465 cos a.
v = 465 x cos 38,94 ~362 m /s.
2.1. Montrer que dans le référentiel terrestre la vitesse moyenne de l'ombre de la lune sur la terre est d'environ 750 m /s.
Distance Colombia - Charleston ~1300 km.
Ombre de la lune à Colombia : 18 h 20.
Ombre de la lune à Charleston : 18 h 47 mn.
Durée du parcours : 27 min ou 1620 s.
V0 = 1390 / 1620 ~0,80 km /s.
2.2.Compte
tenu de la durée maximale de l'éclipse en un lieu de son passage,
estimer le diamètre de l'ombre de la lune sur la terre lors de
l'eclipse.
A Colombia comme à Charleston, la durée de l'eclipse est d'environ 2 min 38 s ou 158 s.
0,75 *158 ~ 119 km.
3. Mouvement de la lune autour de la terre.
3.1. Pourquoi ne tient-on pas compte du phénomène de diffration des rayons lumineux par la lune ?
Valeur moyenne de la longueur d'onde de la lumière solaire~0,6 µm.
Diamètre de l'obstacle lune : 3747 km.
Pour observer un phénomène de diffraction, les dimensions de l'obstacle
doivent être de l'ordre de grandeur de la longueur d'onde de la lumière.
3.2 et 3
Faire un schéma sur lequel apparaîtront la terre, la lune et son orbite
supposée circulaire. Représenter la force modélisant l'interaction
gravitationnelle exercée par la terre sur la lune. Donner l'expression
de cette force.
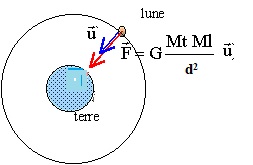
3.4 Etablir l'expression vectorielle de l'accélération de la lune, en fonction de G, Mt, d et du vecteur unitaire.
Ecrire la seconde loi de Newton, la lune étant soumise uniquement à la force de gravitation terrestre.
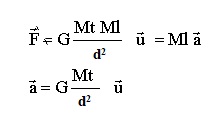
3.5. Montrer que la vitesse de la lune sur son orbite s'exprime par : v = (GMt / d)½.
L'accélération est centripète : a = v2 / d = GMt / d2 ; par suite : v = (GMt / d)½.
3.6. Calculer la valeur de cette vitesse.
v = (6,67 10-11 x5,97 1024 / (3,84 108))½ =1,02 103 m /s.
|
|
|
Partie B. Etude de la couronne solaire.
1.1. Le spectre donné de la couronne solaire est-il un spectre d'émission ou d'absorption ? Justifier.
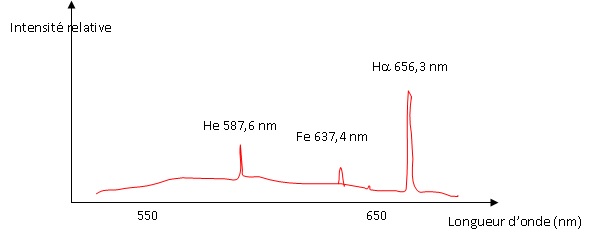
Il s'agit d'un spectre
d'émission. On observe le spectre continu de la lumière blanche et 3
raies brillantes caractéristiques de 3 éléments présents dans la
couronne. Dans le cas d'un spectre d'absorption, on observerait sur
fond continu de l'arc en ciel, des raies noires.
1.2. A quel domaine du spectre électromagnétique ce spectre appartient-il ? Justifier.
Ce spectre s'étend de 500 nm à 700 nm ; il appartient donc au domaine visible [ 400 nm ; 800 nm ].
Extrait du diagramme énergétique de l'atome d'hélium.
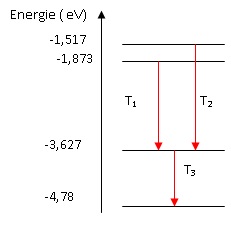
1.3 A quelle transition la radiation émise par l'hélium appartient-elle ?
DE =h c / l = 6,63 10-34 x3 108 /(587,6 10-9) = 3,385 10-19 J ou 3,385 10-19 / (1,6 10-19) = 2,11 eV.
Or 3,627 -1,517 = 2,11 eV.
Il s'agit de la transition T2.
1.4. Histotiquement cette
radiation a été confondue avec celle émise par le sodium : 589,0 et
589,6 nm. L'utilisation d'un spectromètre dont l'incertitude relative
est U(l) / l = 10-3 permet-elle de discerner la radiation émise par l'hélium de celles émises par le sodium ?
589-587,6=1,4 et 1,4 / 589 =2,4 10-3 ;
l'écart relatif étant supérieur à 10-3, la raie de l'hélium peut être discerner de celles du sodium.
|
|
|
|
2. Le mystère de la couronne solaire.
La couronne solaire est formée de jets de matière, principalement d'hydrogène et d'hélium, issus de la surface du soleil.
Les astrophysiciens disposent de plusieurs méthodes pour déterminer la température d'un corps.
Loi de Wien : lmax = 2,9 10-3 / T ( en m).
Elargissement des raies spectrales : à mi-hauteur pour l'élément hydrogène, la largeur d'une raie Dl = 7,2 10-7 l0 T½ = 0,5 nm
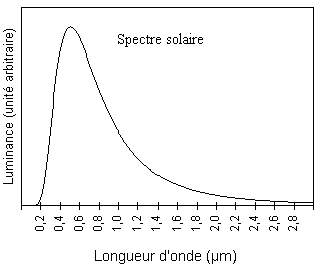
2.1. Comparer les températures de la couronne solaire et de la surface du soleil.
Surface du soleil : lmax ~0,5 10-6 m.
La loi de Wien conduit à : T = 2,9 10-3 / (0,5 10-6) ~5,8 103 K.
Couronne : T½ = Dl / ( 7,2 10-7 l0 ) = 0,5 /(7,2 10-7 x656,3) = 1058 ; T ~ 1,1 106 K.
La température de la couronne est très supérieure à celle de la surface du soleil.
2.2. A quel problème sont confrontés les astrophysiciens dans l'estimation de ces températures ?
L'atmosphère terrestre absorbe certaines radiations de la lumière solaire.
|
|
|