Modélisation
d'un parachute, Bac S Amérique du Nord 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
L'étude de la chute d'une boule de pétanque attachée à un petit parachute est conduite au laboratoire.
Physique du parachutiste.
Pour qu'un parachute soit efficace, il doit diminuer la vitesse limite d'au moins 75 %.
1. Cadre théorique de l'étude.
On considère le système boule de pétanque + parachute.
La masse de la boule étant très supérieure à celle du parachute, on
assimile la masse du système à celle de la boule de pétanque. le volume
de la toile du parachute ainsi que celui des fils seront négligés. Seul
sera pris en compte le volume de la boule.
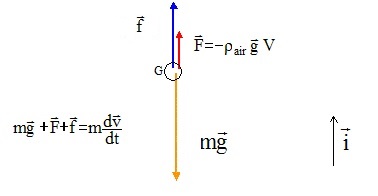
Le système en chute est soumis :
à son poids P = mg avec m = 400 g;
à l'action mécanique de l'air noté f ;
à la poussée d'Archimède notée F= rair V g avec V : volume de la boule, g = 9,8 m s-2 et rair = 1,2 kg m-3.
Diamètre de la boule d = 10 cm.
1.1. Ecrire la seconde loi de Newton appliquée au système étudié.
1.2. Montrer que l'on peut négliger la poussée devant le poids.
P = mg = 0,400 x9,8 ~3,9 N.
Volume de la boule V =4 / 3 p r3= 4 / 3 *3,14 x0,053 = 5,23 10-4 m3.
F = 1,2 x5,23 10-4 x9,8 ~0,0061 N, valeur environ 600 fois plus petite que celle du poids
2. Etude expérimentale.
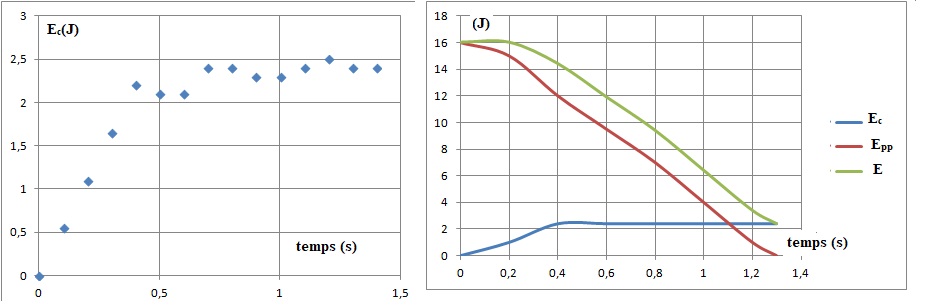
L'énergie potentielle de pesanteur est choisie nulle au sol.
|
|
.
.
|
|
2.1. Comment évolue la vitesse du système lors de sa chute ? Justifier.
Jusqu'à 0,4 s, l'énergie cinétique croît ; elle reste constante ensuite.
La vitesse croît jusqu'à t = 0,4 s puis elle reste constante.
2.2 Estimer la valeur de la vitesse limite. A partir de quelle date cette vitesse est-elle atteinte ?
Ec max = 2,4 =0,5 mv2lim ; vlim = (2,4 x2 / 0,4)½~3,5 m /s.
2.3 En s'appuyant sur l'expression de l'énergie potentielle de pesanteur du système, déterminer la valeur Dz de la variation d'altitude du système pendant la phase de mouvement uniforme.
Epp varie de 12 J ( à t = 0,4 s ) à zéro.
0-12 = mg Dz ; Dz = -12 /(0,4 x9,8) ~ -3,1 m.
2.4
Comment l'énergie mécanique du système évolue t-elle au cours du
mouvement ? Que peut-on en conclure sur les forces de frottement
de l'air exercées sur le système ?
Jusqu'à t = 0,2 s, l'énergie mécanique du système reste à peu près
constante. Puis l'énergie mécanique diminue de 16 J à 2,0 J. Les forces
de frottement due à l'air doivent être prise en compte.
2.5. Déterminer la variation de l'énergie mécanique du système durant la phase de mouvement uniforme.
DE = 2,4-14,5 = -12,1 J.
2.6.
En déduire la valeur de la force de frottement supposée constante
pendant la phase de mouvement uniforme. Conclure quand au bilan des
forces durant cette phase.
La variation de l'énergie mécanique est égale au travail des frottements :
-12,1 = f Dz ; f = -12,1 / (-3,1) ~3,9 N.
Pendant cette phase de mouvement rectiligne uniforme, le poids et les frottements se compensent.
|
|
3. Pour aller plus loin....
On
reproduit cette expérience de chute dans un tube vertical dans lequel
on a fait le vide. Les conditions initiales sont identiques..
Représenter
l'allure de l'évolution, au cours du temps, des énergies cinétique,
potentielle de pesanteur et mécanique. Justifier l'allure de ces
courbes en donnant leurs équations horaires..
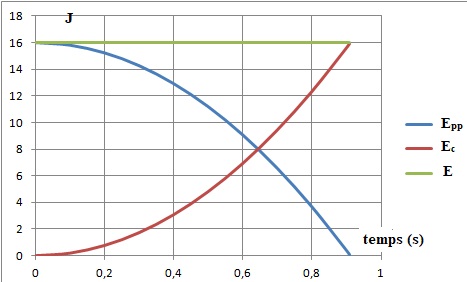
En absence d'air, les frottements sont nuls.
La chute est verticale, libre, sans vitesse initiale.
v = -gt ; z = -½gt2 + z0.
Epp = mgz = mg(-½gt2 + z0)
Ec = ½mv2=0,5 m(gt)2= 0,5 x0,4 x9,82 t2 = 19,2 t2.
E = Ec + Epp = 16= Epp(t=0) = mgz0 ; z0 = 16 / (0,4 x9,8) ~4,1 m.
Epp = -19,2t2 + 16.
|
|