Mathématiques,
Brevet Asie 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
.
.
|
|
Exercice
1.
Une
entreprise a enregistré, pour chaque mois de l’année 2016, le
pourcentage de commandes livrées en retard. Le diagramme suivant
présente ces données.
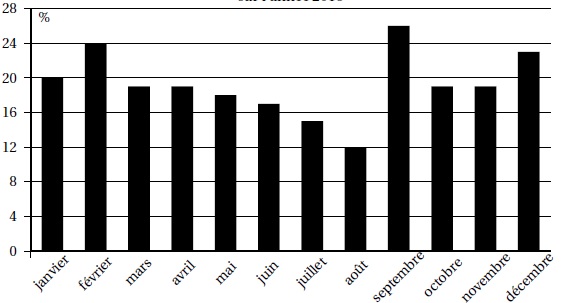
1. Quel est le mois de l’année où le pourcentage de commandes livrées en retard a été le plus important ?
Aucune justification n’est attendue.
Septembre.
2. Pour quels mois de l’année ce pourcentage a-t-il été inférieur ou égal à 18% ?
Aucune justification n’est attendue.
Mai, juin, juillet, aout.
3. Quelle est l’étendue de cette série de données ?
La plus grande valeur - la plus petite = 26-12 = 14.
Exercice 2 .
Samia vit dans un appartement dont la surface au sol est de 35 m2.
Elle le compare avec une yourte, l’habitat traditionnel mongol.
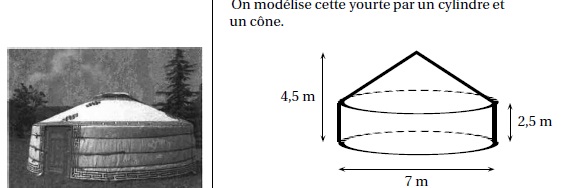
1. Montrer que l’appartement de Samia offre une plus petite surface au sol que celle de la yourte.
Aire d'un disque pR2 = 3,14 x3,52 ~38,5 m2, valeur supérieure à 35 m2.
2. Calculer le volume de la yourte en m2.
Volume du cylindre : p R2 h = 3,14 x3,52 x2,5 = 96,2 m3.
Volume du cône : p R2 h / 3= 3,14 x3,52 x2 / 3 = 25,66 m3.
Total : 121,8 ~122 m3.
3. Sarnia réalise une maquette de cette yourte à l’échelle 1 / 25 .
Quelle est la hauteur de la maquette ?
4,5 / 25 = 0,18 m = 18 cm.
Exercice 3. QCM.
L’écriture décimale du nombre 5,3×105 est :
530 000 ( vrai) ; 5,300 000 ; 5 300 000.
Un dé équilibré a six faces numérotées de 1 à 6.
On souhaite le lancer une fois. La probabilité d’obtenir un diviseur de 20 est :
2 /3 ( vrai) ; 4 /20 ; 1 /2.
Diviseurs de 20 inférieurs ou égal à 6 : 1 ; 2 ; 4 ; 5.
4 cas favorables sur 6 possibilités.
4 / 6 = 2 / 3.
L’égalité (x +5)2 = x2 +25.
n'est vraie pour aucune valeur de x ; est vraie pour une valeur de x (vrai) ; ; est vraie pour toute valeur de x.
x2 +10x +25 = = x2 +25.
10 x = 0 soit x = 0.
On veut remplir des bouteilles contenant chacune 3 / 4 L.
Avec 12 L, on peut remplir 9 bouteilles, 12 bouteilles ; 16 bouteilles ( vrai).
12 / 0,75 = 16.
|
|
Exercice 4.
Arthur doit écrire un programme avec Scratch pour dessiner une étoile comme le dessin représenté ci-dessous.
Il manque dans son programme le nombre de répétitions.
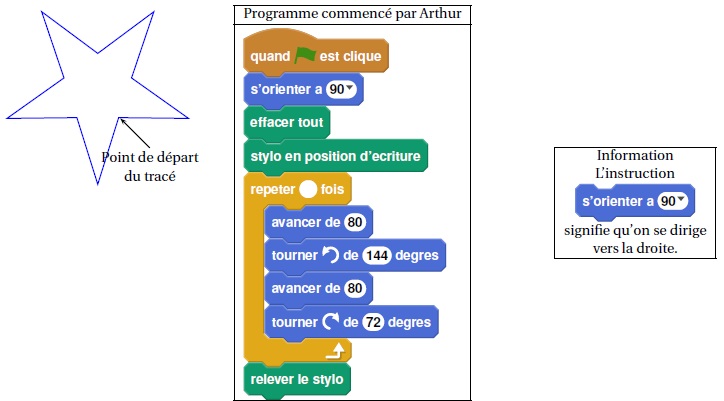
1. Quel nombre doit-il saisir dans la boucle « répéter » pour obtenir l’étoile ?
5, l'étoile compte cinq branches..
2. Déterminer le périmètre de cette étoile.
80 x10 = 800
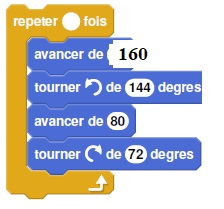
3. Arthur souhaite agrandir cette étoile pour obtenir une étoile dont le périmètre serait le double, en modifiant son programme.
Recopier la partie du programme cicontre sur la copie en modifiant les valeurs nécessaires pour obtenir cette nouvelle étoile.
Exercice 5.
Paul
veut construire un garage dans le fond de son jardin. Sur le schéma
suivant, la partie hachurée représente le garage positionné
en limite de propriété. Les longueurs indiquées (1,6 m et 3 m) sont
imposées ; la longueur marquée par un point d’interrogation est
variable.
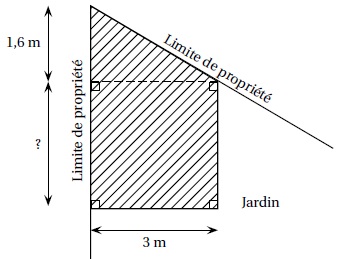
Sachant que la surface du garage ne doit pas dépasser 20 m2, quelle valeur maximale peut-il choisir pour cette longueur variable ?
Aire de la partie triangulaire : 1,6 x 3 / 2 =2,4 m2.
Aire du quadrilatère : 3 x = 20-2,4 = 17,6 m2.
x = 17,6 / 3 ~5,87 m.
|
|
Exercice 6.
Avec
un logiciel de géométrie dynamique, on a construit la figure A. En
appliquant à la figure A des homothéties de centre O et de rapports
différents, on a ensuite obtenu les autres figures.
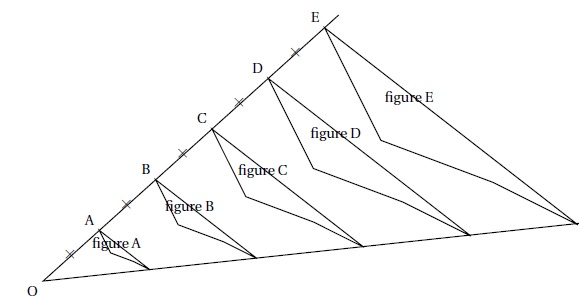
1.
Quel est le rapport de l’homothétie de centre O qui permet d’obtenir la
figure C à partir de la figure A ? Aucune justification n’est attendue.
OC / OA = 6 /2 = 3.
2. On applique l’homothétie de centre O et de rapport 3 / 5 à la figure E. Quelle figure obtient-on ?
Aucune justification n’est attendue.
OE x 3 / 5 = 3, figure C.
3. Quelle figure a une aire quatre fois plus grande que celle de la figure A ?
Les mesures des côtés doivent être le double de celles de A, donc figure B.
Exercice 7.
Francis veut se lancer dans la production d’oeufs biologiques. Son terrain est un rectangle de 110 m de long et 30 m de large.
Il va séparer ce terrain en deux parties rectangulaires
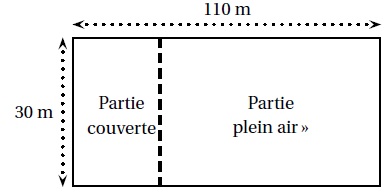
Pour avoir la qualification « biologique », Francis a l’obligation de respecter les deux règles ci-dessous.
Partie couverte : utilisée pour toutes les poules quand il fait nuit , 6 poules maximum par m2.
Partie « Plein air » : utilisée pour toutes les poules quand il fait jour , 4 m2 minimum par poule.
Il a prévu que la partie couverte ait une surface de 150 m2.
1. Montrer que l’aire de la partie « plein air » est de 3 150 m2.
Partie couverte : 30 x = 150 ; x = 150 / 30 = 5 m.
Aire de la partie plein air : 30 *(110-5) = 3 150 m2.
2. Peut-il élever 800 poules dans son installation ?
Nombre maximum de poules dans la partie couverte : 150 x6 = 900.
Nombre maximum de poules dans la partie plein air : 3150 / 4 =787,7 ( 787).
Non, il ne peut pas élever 800 poules.
3. Combien de poules au maximum pourrait-il élever dans son installation?
787.
Exercice 8.
Lorsqu’on fait geler de l’eau, le volume de glace obtenu est proportionnel au volume d’eau utilisé.
En faisant geler 1,5 L d’eau on obtient 1,62 L de glace.
1. Montrer qu’en faisant geler 1 L d’eau, on obtient 1,08 L de glace.
1,62 x1 / 1,5 = 1,08 L.
2. On souhaite compléter le tableau ci-dessous à l’aide d’un tableur.
Quelle formule peut-on saisir dans la cellule B2 avant de la recopier vers la droite jusqu’à la cellule G2 ?

=B1*1,08
3. Quel graphique
représente le volume de glace obtenu (en L) en fonction du volume d’eau
contenu dans la bouteille au départ (en L) ?
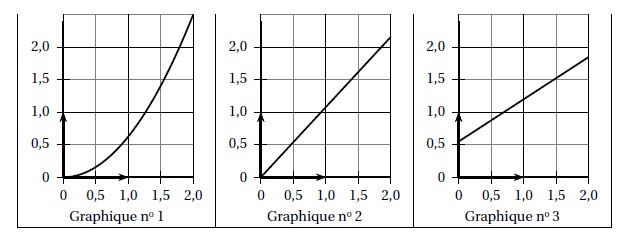
Le volume de glace obtenu est proportionnel au volume d’eau utilisé.
Lorsque deux grandeurs sont propotionnelles, le graphe correspondant est une droite passant par l'origine.
Le graphe n°2 représente le volume de glace obtenu (en L) en fonction du volume d’eau.
|
|