Mathématiques,
Brevet Polynésie 09 /2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
Exercice
1. 12 points
Indiquer si les affirmations suivantes sont vraies ou fausses.
Justifier vos réponses.
Affirmation 1.
On lance un dé équilibré à six faces numérotées de 1 à 6. Un élève
affirme qu’il a deux chances sur trois d’obtenir un diviseur de 6.
A-t-il raison ? Faux.
Un cas favorable sur six cas possibles; la probabilité d'obtenir 6 est
égale à 1 / 6.
Affirmation 2.
On considère le nombre a=34×7.
Un élève affirme que le nombre b=2×35×72 est un
multiple du nombre a. A-t-il raison ? Vrai.
b = 2 x3 x34 x7 x7 = 42 a.
Affirmation 3.
En 2016, le football féminin comptait en France 98 800 licenciées alors
qu’il y en avait 76 000 en 2014.
Un journaliste affirme que le nombre de licenciées a augmenté de 30 %
de 2014 à 2016. A-t-il raison ? Vrai.
(98 800 -76 000) / 76 000 x100 = 30 %.
Affirmation 4.
Une personne A a acheté un pull et un pantalon de jogging dans un
magasin. Le pantalon de jogging coûtait 54 €. Dans ce magasin, une
personne B a acheté le même pull en trois exemplaires ; elle a dépensé
plus d’argent que la personne A. La personne B affirme qu’un pull coûte
25 €. Faux.
A-t-elle raison ?
On note x le prix du pull : 54 +x = yA.
3x = yB ; 3x > 54 +x ; 2x > 54 ; x > 27.
Exercice 2. 14
points.
Un
amateur de football, après l’Euro 2016, décide de s’intéresser à
l’historique des treize dernières rencontres entre la France et le
Portugal, regroupées dans le tableau ci-dessous.
On rappelle la signification des résultats ci-dessous en commentant
deux exemples :
la rencontre du 3 mars 1973, qui s’est déroulée en France, a vu la
victoire du Portugal par 2 buts à 1 ;
la rencontre du 8 mars 1978, qui s’est déroulée en France, a vu la
victoire de la France par 2 buts à 0.
3
mars 1973
|
France
Portugal
|
1
- 2
|
26
avril 1975
|
France
Portugal |
0
- 2
|
8
mars 1978
|
France
Portugal |
2
-0
|
16
février 1983
|
Portugal
- France
|
0
- 3
|
16
juin 1984
|
France
Portugal |
3
- 2
|
24
janvier 1996
|
France
Portugal |
3
- 2
|
22
janvier 1997
|
Portugal
France
|
0
- 2
|
28
juin 2000
|
Portugal
France
|
1
- 2
|
25
avril 2001
|
France
Portugal |
4
- 0
|
5
juillet 2006
|
Portugal
France
|
0
- 1
|
11
octobre 2014
|
France
Portugal |
2
- 1
|
4
septembre 2015
|
Portugal
France
|
0
- 1
|
10
juillet 2016
|
France
Portugal |
0
- 1
|
1. Depuis 1973, combien de fois la
France a-t-elle gagné contre le Portugal ? 10 fois.
2. Calculer le
pourcentage du nombre de victoires de la France contre le Portugal
depuis 1973. Arrondir le résultat à l’unité de %.
10 victoires en 13 matchs : 10 / 13 x 100 ~77 %.
3. Le 3 mars 1973,
3 buts ont été marqués au cours du match. Calculer le nombre moyen de
buts par match sur l’ensemble des rencontres. Arrondir le résultat au
dixième.
35 buts en 13 rencontres : 35 / 13 =2,7.
Exercice 3 . 16
points.
Une
personne s’intéresse à un magazine sportif qui parait une fois par
semaine. Elle étudie plusieurs formules d’achat de ces magazines qui
sont détaillées ci-après.
Formule A - Prix du magazine à l’unité : 3,75 € ;
Formule B - Abonnement pour l’année : 130 € ;
Formule C - Forfait de 30 € pour l’année et 2,25 € par magazine.
On donne ci-dessous les représentations graphiques qui correspondent à
ces trois formules.
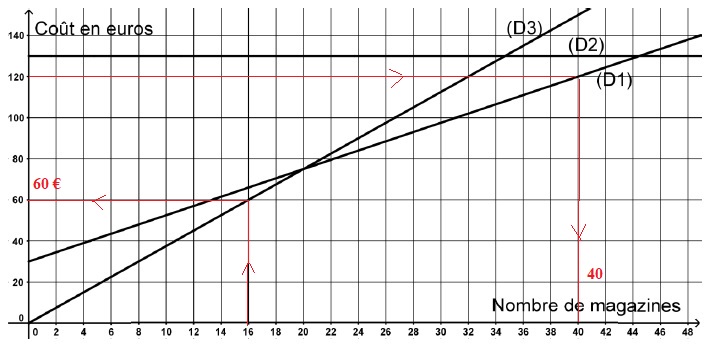
1. Sur votre copie,
recopier le contenu du cadre ci-dessous et relier chaque formule
d’achat avec sa représentation graphique.
Formule A : D3.
Formule B : D2.
Formule C : D1.
2. En utilisant le
graphique, répondre aux questions suivantes.
Les traits de construction devront apparaitre sur le graphique.
a. En choisissant
la formule A, quelle somme dépense-t-on pour acheter 16 magazines dans
l’année ? 60 €
b. Avec 120 €,
combien peut-on acheter de magazines au maximum dans une année avec la
formule C ?
c. Si on décide de
ne pas dépasser un budget de 100 € pour l’année, quelle est alors la
formule qui permet d’acheter le plus grand nombre de magazines ?
Formule C ( 31 magazines ) ; formule A ( 27 magazines).
3. Indiquer la
formule la plus avantageuse selon le nombre de magazines achetés dans
l’année.
Si on achète plus de 45 magazines : formule B
Si on achète moins de 19 magazines : formule A.
Si on achète entre 19 et 45 magazines : formule C.
Exercice
4. 14 points.
Un
garçon et une fille pratiquent le roller. Ils décident de faire une
course en empruntant deux parcours différents. La fille, qui part du
point F et arrive au point A, met 28,5 secondes. Le garçon, qui part du
point G et arrive aussi au point A, met 28 secondes.
Le dessin ci-après, qui n’est pas à l’échelle, représente les deux
parcours ; celui de la fille comporte deux demi-cercles de 5 m de rayon.
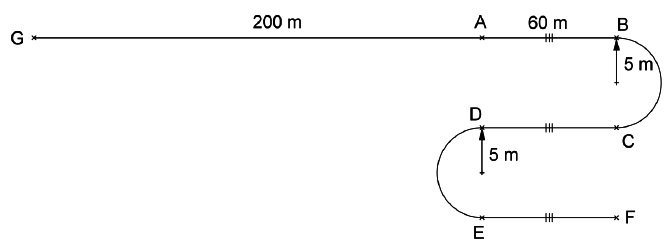
1. Quel est le
parcours le plus long ?
Parcours de la fille : 3 x 60 + 2 x5 x3,14 = 180 +31,4 = 211,4 m.
Parcours du garçon : 200 m.
Le parcours de la fille est le plus long.
2. Qui se déplace
le plus vite, le garçon ou la fille ?
Vitesse de la fille : 211,4 / 28,5 ~ 7,4 m /s.
Vitesse du garçon : 200 / 28 ~ 7,1 m /s.
La fille se déplace le plus vite.
|
|
|
|
|
Exercice
5. 14 points.
Un collégien français et son correspondant anglais ont de nombreux
centres d’intérêt communs comme le basket qu’ils pratiquent tous les
deux.
On donne quelques informations sur leurs ballons.
Ballon du collégien français : aire de la surface du ballon A ~
1950 cm2.
Ballon du correspondant anglais : diamètre du ballon D = 9,5 inch ( 1
inch = 2,54 cm).
Pour qu’un ballon soit utilisé dans un match officiel, son diamètre
doit être compris entre 23,8 cm et 24,8 cm.
1. Le ballon du
collégien français respecte-t-il cette norme ? Non.
4 x 3,14 x r2 = 1950 ; r2 ~1950 / (4 x3,14) ~
155,17 ; r = 12,46 cm ; 2r = 24,9 cm.
2. Le ballon du
collégien anglais respecte-t-il cette norme ? Oui.
9,5 x 2,54 =
24n13 cm.
Exercice 6. 12 points.
Une
personne pratique le vélo de piscine depuis plusieurs années dans un
centre aquatique à raison de deux séances par semaine. Possédant une
piscine depuis peu, elle envisage d’acheter un vélo de piscine pour
pouvoir l’utiliser exclusivement chez elle et ainsi ne plus se rendre
au centre aquatique.
Prix de la séance au centre aquatique : 15 €.
Prix d’achat d’un vélo de piscine pour une pratique à la maison : 999
€.
1. Montrer que 10
semaines de séances au centre aquatique lui coûtent 300 €.
10 x 2 x15 = 300 €.
2. Que représente
la solution affichée par le programme ci-après ?
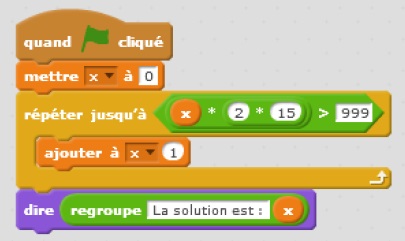
La soluion du programme donne le nombre de semaines à partir duquel, le
vélo est amorti.
3. Combien de
semaines faudrait-il pour que l’achat du vélo de piscine soit
rentabilisé.
30 x = 999 ; x = 999 / 30 = 33,3. soit 34 semaines.
|
|
Exercice 7. 18 points.
Une personne possède une piscine. Elle veut coller une frise en
carrelage au niveau de la ligne d’eau.
La piscine vue de haut, est représentée à l’échelle par la partie
grisée du schéma ci-après.
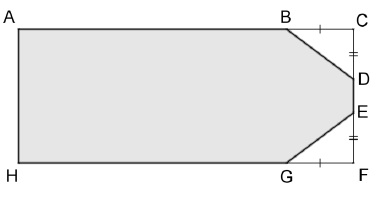
Données
:
le quadrilatère ACFH est un rectangle ;
le point B est sur le côté [AC] et le point G est sur le côté [FH] ;
les points D et E sont sur le côté [CF] ;
AC = 10 m ; AH = 4 m ; BC = FG = 2 m ; CD = EF = 1,5 m.
Question : Calculer la longueur de la frise.
2 AB + 2 BD +DE.
AB = 10 -2 = 8 m ;
DE = 4 -2 x1,5 = 1 m.
BD2 = BC2 +CD2 = 4 +2,25 = 6,25 ; BD =
2,5 m.
Longueur de la frise : 16 + 5 +1 = 22 m.
2ème
partie.
La personne décide d’installer, au-dessus de la piscine, une grande
voile d’ombrage qui se compose de deux parties détachables reliées par
une fermeture éclair comme le montre le schéma ci-dessous qui n’est pas
à l’échelle.
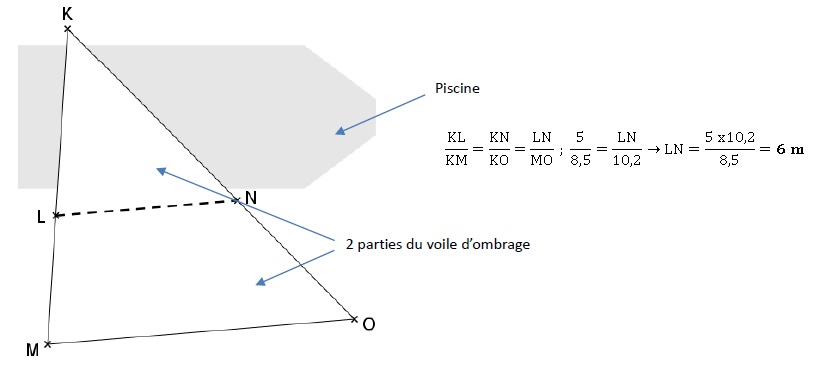
Données :
la première partie couvrant une partie de la piscine est représentée
par le triangle KLN ;
la deuxième partie est représentée par le trapèze LMON de bases [LN]
et [MO] ;
la fermeture éclair est représentée par le segment [LN] ;
les poteaux, soutenant la voile d’ombrage positionnés sur les points
K, L et M, sont alignés ;
les poteaux, soutenant la voile d’ombrage positionnés sur les points
K, N et O, sont alignés ;
KL = 5 m ; LM = 3,5 m ; NO = 5,25 m ; MO = 10,2 m.
Question : Calculer la longueur de la fermeture éclair.
|
|