QCM
mathématiques,
concours Avenir 2018.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
Répondre à 45 questions
au choix parmi les 60 proposées. Sans cakculatrice.
Une
seule réponse exacte par question ; chaque réponse exacte rapporte + 3
points ; chaque réponse fausse enlève 1 point.
Statistiques.
Tour
les questions 1 à 4, on considère deux séries statistiques, A et B,
dont on a les diagrammes de TUKEY (diagrammes en boites). Les valeurs
extrêmes de chaque diagramme sont le minimum et le maximum de chaque
série.
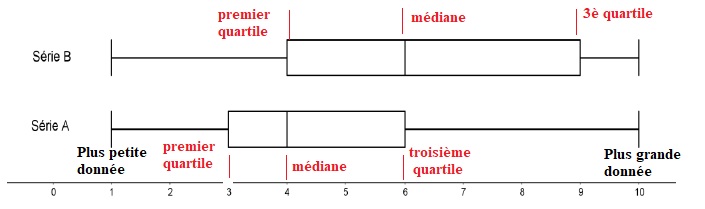 1. Les deux séries ont :
1. Les deux séries ont :
a : la même médiane.
b : la même
étendue. Vrai.
c : le même écart interquartiles.
d : Aucune des réponses précédentes n’est juste.
2. Laquelle des
propositions suivantes est vraie ?
a : Les valeurs des deux séries sont également dispersées.
b : Les valeurs de la série A sont plus dispersées que les valeurs de
la série B.
c : Les valeurs de
la série B sont plus dispersées que les valeurs de la série A. Vrai.
d : Il n’y a pas assez d’informations pour comparer la dispersion des
valeurs des deux séries..
La série A est plus
concentrée ( boîte moins large ). L'intérieur des boîtes correspond à
50 % des élèves.
3. Laquelle
des propositions suivantes est vraie ?
a : 50% des valeurs de la série A sont supérieures ou égales à 50% des
valeurs de la série B.
b : 75 % des valeurs de la série A sont supérieures ou égales à 25 %
des valeurs de la série B.
c : 50% des valeurs de la série B sont inférieures ou égales à 50% des
valeurs de la série A.
d : 75 % des valeurs de la série A sont inférieures ou égales à 50 %
des valeurs de la série B. Vrai.
Le troisième quartile de
la série A correspond à la médiane de la série B.
4. On note respectivement xA
moy et xB moy la moyenne arithmétique de la série A
et de la série B.
a : xA moy =
xB moy
b
: xA moy <
xB moy
c
: xA moy >
xB moy
d : Il n’y a pas assez
d’informations pour comparer les moyennes. Vrai.
Logique.
Pour les questions 5 à 8, on note P et Q deux propositions, elles
peuvent être chacune et de façon indépendante vraie ou fausse.
5.
On note P ^Q la conjonction des propositions P et Q , P ^Q n’est vraie
que lorsque P et Q sont vraies toutes les deux. Laquelle des
propositions suivantes est fausse ?
a : "25 = 32" ^" ln(0,5 <0".
b : " e4 = 32" ^"|2+i| = 5". Faux.
c : "7½ < 3" ^"e-3 >0".
d : "cos 45 ~0,707" ^ "15 / 9 >1".
6. On
note P v Q la disjonction des propositions P et Q, P v Q n’est fausse
que lorsque P et Q sont fausses toutes les deux. Laquelle des
propositions suivantes est fausse ?
a : " 22 = 25" v " ln(1 / e) < 0,4".
b : "e4 >e2" v "(3+i)2 = 8 +
6i".
c : " 17½
< 3 " v "e-5 > 1". Vrai.
d : " cos 60 = 0,5" v "20½ > 2 x5½".
7.
On note P = > Q l’implication de Q par P, P = > Q est fausse si
et seulement si P est vraie et Q est fausse. Laquelle des propositions
suivantes est vraie ?
a : " 23 = 8 " = > "ln3
<0".
b : " e4 > 1" = > 72 < e4".
c : "sin 180 = 0" = > " pour tout x réel non nul, 1 /x < x".
d : e4
< 0" = > "32 = 9". Vrai.
8.
On note P < = > Q l’équivalence entre les propositions P et Q,
n’est vraie que lorsque Pet Q sont vraies toutes les deux ou fausses
toutes les deux. Laquelle des propositions suivantes est fausse ?
a : "i2 = 1" < => " e < 1".
b : "e4 >1" < = > "le conjugué de (2i+3) est 3-2i".
c : "i5
= i" < = > "ln(2) <0". Vrai.
d : " cos 45 ~0,866" < = > "4 / 7 > 2".
Loi binomiale.
Pour
les questions 9 à 12, on considère une variable aléatoire X qui suit
une loi binomiale B( n ; 0,2) où est un entier naturel non nul.
9. L’espérance mathématique de X est : .
a : n.
b : n / 0,2.
c : 0,8 n.
d : n / 5 ( ou 0,2
n). Vrai.
10. P(X=1) =
a : n x 0,2n-1 x0,8.
b : n x 0,2 x0,8n-1.
Vrai.
c : (n-1) x0,2 x0,8n.
d : (n-1) x0,2 x0,8n-1.
p= 0,2 ; 1-p = q = 1-0,2
= 0,8 ; P(X=1) = n p1 qn-1.
11. Si on veut que
P(X=0) = 0,512, alors il faut que :
a : n = 2
b : n = 3. Vrai.
c : n = 4.
d : Aucune des réponses précédentes n’est juste.
P(X=1) = n p1 qn-1
= 1 x0,20 x0,8n
= 0,512 ; n ln(0,8) = ln(0,512) ; n ~3.
12 : Si on veut que l’écart-type de
X soit égal à 0,8, alors il faut que :
a : n = 2.
b : n = 3.
c : n = 4. Vrai.
d : Aucune des réponses précédentes n’est juste.
écart type = ( n p q)½ =0,8
; n x 0,2 x0,8 = 0,8 x0,8 ; n = 0,8 / 0,2 = 4.
|
|
|
|
Suites.
Pour les questions 13 à 19, on considère la fonction f, définie,
continue et strictement croissante sur R représentée en trait plein
ci-dessous. Sur le même graphique est représentée la droite d’équation
réduite y = x en traits pointillés.
Pour tout x appartenant à [-4 ; 3 ], f(x) < x, sinon
f(x) > x.
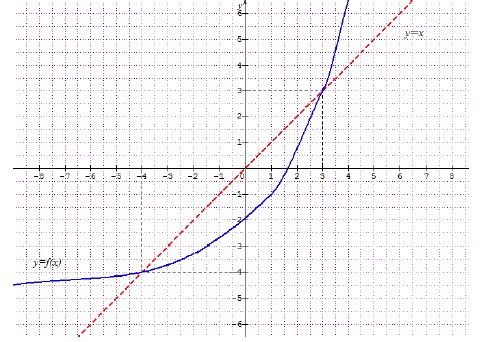
On considère la suite définie par u0 réel et un+1
= f(un).
13 : Si u0
= 4 alors la limite de un en plus l'infini est :
a : 3
b : -4. Vrai.
c : +oo
d : -oo.
u1
=f(4) ~7 u2 = f(-1) ~ -2,6 ; u3
= f(-2,6) ~ -3,5 ; u4 = f(-3,5) ~ -3,8 ; u5
= f(-3,8) ~-3,9 ; u6 = f(-3,9) ~ -4 ; u7
= f(-4) = -4.
14) Si u0 = 4 alors la limite de un en plus
l'infini est :
a : 3
b : -4.
c : +oo. Vrai.
d : -oo.
15. Si u0 = -6, alors la
limite en plus l'infini de e-2un est :
a : e-6.
b : e8.
Vrai.
c : +oo.
d ; 0.
e-2u0 =e12 ; u1 = f(-6) ~ --4,2 ; e-2u1 ~e8,4 ;u2 = f(--4,2) ~ -4 ; e-2u2 ~e8 .
16 Si u0 > 3 alors la
suite vn définie par vn = un-1 / un+1
pour n entier est :
a : strictement
croissante. Vrai.
b : strictement
décroissante.
c : non monotone.
d : Aucune des réponses précédentes n’est juste.
vn+1-vn =
17)
Si u0 < -4 alors la suite vn
définie par vn = un+1 / un-1 pour n
entier est :
a : strictement
croissante.
b : strictement décroissante. Vrai.
c : non monotone.
d : Aucune des réponses précédentes n’est juste.
18 Laquelle des propositions
suivantes est vraie ?
a : La suite (un) est toujours strictement croissante, quel
que soit le choix de u0
b : La suite (un) est toujours strictement décroissante,
quel que soit le choix de u0.
c : Il est possible de choisir u0 pour que la limite en plus
l'infini de un soit moins l'infini.
d : Il est possible de choisir u0
pour que la limite en plus l'infini de 4-5un soit moins
l'infini. Vrai.
.
19 Laquelle des
propositions suivantes est vraie ?
a : Il est possible de choisir u0 pour que la suite (un)
soit arithmétique de raison strictement positive et convergente vers 3.
b : Il est possible de choisir u0
pour que la suite (un)
soit arithmétique de raison strictement négative.
c : Il est possible de choisir u0
pour que la suite (un)
soit géométrique de raison appartenant à ]-1 ; +1[.
d : Aucune des
réponses précédentes n’est juste. Vrai.
Nombres
complexes.
Pour les questions 20 à 26, on se place dans le plan complexe muni d’un
repère orthonormé . On considère les points A, B, C, D, E, F, G et H
d’affixes respectifs zA, zB, zC, zD,
zE, zF, zG et zH. Tous les
points se trouvent exactement à l’intersection d’un cercle et d’un
rayon. L’angle entre 2 rayons consécutifs est constant.
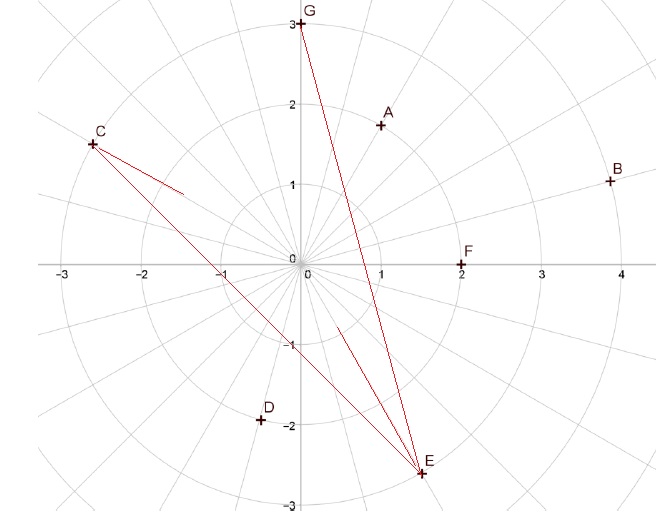
20 La valeur dans
]- p : + p[ de l'argument de zA
est :
a ; p /6.
b: 5p / 12.
c : p /3. Vrai.
d : 3p / 12.
zA = 2 exp(i 4
p /
12) = 2 exp (i p
/3).
21
La valeur dans ]- p
: + p[ de
l'argument de zC x zD est :
a ; p.
b: 3p / 12. Vrai.
c : p /2.
d : 7p / 12.
zC
= 3 exp(i 10 p /
12) ; zD = 2 exp( -7i p / 12) ; zC
x zD = 6 exp (3i p / 12)
22 Le nombre
complexe zE est une racine de :
a : z2-3z-7.
b : z2-3z+1.
c : z2-3z-4.
d : z2-3z+9. Vrai.
zE = 3 exp(-4ip / 12) = 3 exp (-i p /3) = 3( cos(-p
/3) +i
sin(-p
/3) =1,5(1
-i 3½) .
z2E =2,25( 1 +3i2-2i
3½) = -4,5(1 +i 3½)
z2E - 3zE
=-4,5(1 +i 3½)
-4,5 (1 -i 3½) = -9.
23. Le
nombre complexe zB est une solution de :
a : z2 = 8 + 8x3½i.
b : z2 = 8 x3½+ 8i.
c : z2 = 8 - 8x3½i. Vrai.
d : z2 = 8 + 8x3½i.
zB = 4 exp( i p / 12) ;
z2B =16 exp( i p / 6)= 16( cos( p / 6) +i sin(p
/6) =8(3½ + i) .
24. Le
nombre complexe zF / zG est :
a : un nombre réel.
b : un nombre
imaginaire pur. Vrai.
c : un nombre complexe dont ni la partie réelle, ni la partie
imaginaire ne sont nulles.
d : Aucune des réponses précédentes n’est juste.
zF
= 2 ; zG =3 exp( i p / 2) ; zF / zG
= 2 / 3 exp( ( -i p / 2) = -2 /3.
25. La valeur
dans [-p ; +
p) de
l'argument de (zC-zE) / (zG-zE)
est :
a : p / 12.
b : p / 4.
c : p / 6. Vrai.
d : p / 3.
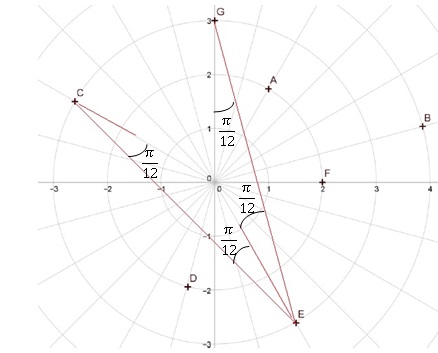
26 : Laquelle des égalités
suivantes est vraie ?
a : zA = exp(ip/4)
x zF.
b : zA
= 2 / 3 exp(-ip/6)
x zG. Vrai.
c
: zA =0,5
exp(ip/6) x zB.
d
:
zA = exp(-11ip/12)
x zD.
zA = 2 exp (i p /3). zF = 2 ; zA
= exp(ip/3) x zF.
zA = 2 exp (i p /3). zG = 3 exp(ip/2) ; zA / zG =2 / 3 exp(-ip/6).
|
|
|
|
|
Fonction exponentielle.
28) Pour tout nombre réel x, on a : 2-(ex+4) / (ex+2)
=
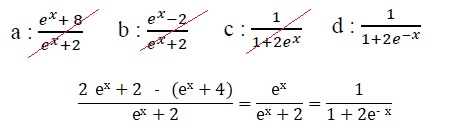
28)
Dans R , l’équation 1 / e2x =e4-x admet pour
solution
a : x = 4 /3.
b : x = -4 /3.
c : x = -4. Vrai.
d :x = 4.
e2x(e4-x)
= 1 ; e2x+4-x= 1 ; ex+4
= 1 ; x+4 = ln 1 = 0 ; x = -4 .
29.
On considère la fonction f définie sur ] -2 ; + oo[ par f(x) = -3e-x
/ (x+2). La fonction fest dérivable sur cet intervalle et f '(x) =
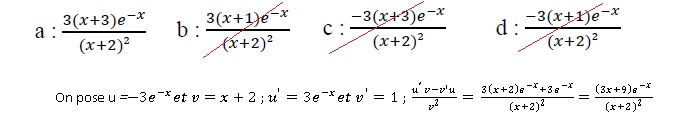
Pour
les questions 30 et 31, on considère les fonctions f et g définies sur
R par f(x) = 0,5(ex+e-x) et g(x) = 0,5(ex-e-x).
30 : Pour tout
nombre réel x , on a : ( f(x))2-(g(x))2 =
a : 1. Vrai.
b : ex.
c : -1
d : e-x.
( f(x))2-(g(x))2
=(f(x) + g(x)) . (f(x)-g(x)) = ex (e-x) = 1.
31 : Pour tous nombres réels x et y
, on a : f(x) *f(y) +g(x) *g(y) =
a :g(x+y).
b : g(x-y).
c : f(x+y). Vrai.
d : f(x-y).
f(x) *f(y)= 0,25(ex+e-x)(ey+e-y)=0,25 (ex+y+e-(x+y)+ex-y
+e-x+y) ;
g(x) *g(y) =0,25(ex-e-x)(ey-e-y)=0,25 (ex+y+e-(x+y)-ex-y
-e-x+y) ;
f(x) *f(y) +g(x) *g(y) =0,5 (ex+y+e-(x+y))=f(x+y).
Trigonométrie.
32 : Dans [0 ; p / 2[, les solutions de
l’équation 2(cos(2x+1)2-1 =0 sont :
a : (7p -4) / 8 et
(9p -4) / 8
b : (3p -1) / 2
et (5p -1) / 2
c :(3p -4) / 8 et (5p -4) / 8. Vrai.
d :
(3p -1) / 4
et (5p -1) / 4.
(2½ cos(2x+1)+1) (2½
cos(2x+1)-1 ) = 0.
cos(2x+1)= -1 / 2½ =
cos(3p / 4) ; 2x +1 = ±3p / 4 + 2k p; x =± 3p / 8 -1 /2 + k p= ( ±3p -4) / 8 +kp ;
Pour k = 1, on retient (5p -4) / 8.
cos(2x+1)= +1 / 2½ = cos(p / 4) ; 2x +1 = ±p / 4 + 2k p; x =± p / 8 -1 /2 + k p= ( ±p -4) / 8 +kp ;
33
: Sur l’intervalle [2017 p /
2 ; 2019 p / 2], la fonction
sinus est :
a : décroissante puis croissante.
b : strictement
décroissante. Vrai.
c : strictement croissante.
d : croissante puis décroissante.
[2017 p / 2 ; 2019 p / 2] = [504 x4 p / 2 +p / 2 ; [504 x4 p / 2 +3p / 2 ] identique à [p / 2 ; 3 p / 2].
Fonction logarithme népérien.
Pour les questions 34 à 40, on considère la fonction g(x) = ln(e2
/(f(x)) où f est une fonction dérivable sur dont le tableau de
variation est le suivant :
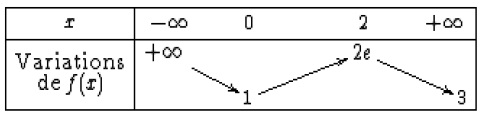
34 : g(0) =
a : 1
b : 2. Vrai.
c : e2.
d : Aucune des réponses précédentes n’est juste.
f(0) = 1 ; g(0) = ln(e2)
= 2 ln (e) = 2.
35 : En plus
l'infini, la limite de g(x) est :
a : -oo.
b : +oo.
c :0.
d : 2-ln(3). Vrai.
En plus l'infini, g(x)
est équivalent à ln(e2 / 3) = 2-ln(3).
36 : En moins
l'infini, la limite de g(x) est :
a : -oo. Vrai.
b : +oo.
c :ln(2) -ln(3).
d : Aucune des réponses précédentes n’est juste.
En moins l'infini, g(x)
est tend vers plus l'infini et e2 /(f(x)) tend vers
zéro ; ln(e2
/(f(x)) tend vers moins l'infini.
37 : La fonction
g(x) est dérivable sur R et g'(x) est donnée par :
a : -e2 f '(x) / f(x).
b : -f '(x) / f(x).
Vrai.
c : -e2 f '(x) / f(x)2.
d : -f '(x) / f(x)2.
On pose u = e2
/(f(x) ; u' = -e2 f '(x) / f(x)2.
Dérivée de ln (u) : u' / u soit -f '(x) / f(x).
38 : Dans le plan
muni d’un repère, la courbe représentative de la fonction g :
a : n’admet aucune asymptote.
b : admet
exactement une asymptote horizontale ou verticale. Vrai.
c : admet exactement deux asymptotes horizontales ou verticales.
d : Aucune des réponses précédentes n’est juste.
En plus l'infini, g(x)
est équivalent à ln(e2 / 3) = 2-ln(3).
39 :
L’équation g(x) = -100.
a : n’admet aucune solution dans R.
b : admet
exactement une solution dans R. Vrai.
c : admet exactement deux solutions dans R.
d : Aucune des réponses précédentes n’est juste.
40 :
L’équation g(x) = 3
a : n’admet aucune
solution dans R . Vrai.
b : admet exactement une solution dans R.
c : admet exactement deux solutions dans R.
d : Aucune des réponses précédentes n’est juste.
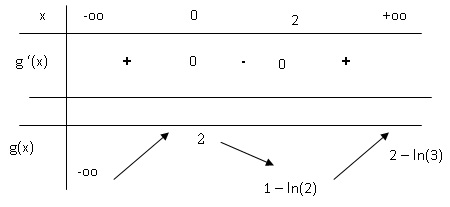
|
|
Intégration.
41) 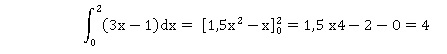
a : 4. Vrai.
b : 5.
c : 6.
d : 10.
42 : 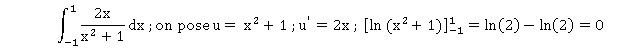
a : 2
b : 0 ,5
c : 0. Vrai.
d : Aucune des réponses précédentes n’est juste.
43 : Pour x
appartenant à [0 ; p
/ 2[ une primitive de tan(x) = sin(x) / cos(x) est
a : -ln(cos(x). Vrai.
b : ln(cos(x).
c : -ln(sin(x).
d : ln(sin(x).
On pose u = cos(x) ; u' = -sin(x) ; une
primitive de u' / u est ln(u) ; la primitive cherchée est -ln(cos(x).
Loi continue.
Pour les questions 44 à 48, on considère une variable aléatoire X à
valeurs dans [1 ; 4 ] qui admet pour densité la fonction f définie pour
tout x de cet intervalle par f(x) = a / x où a appartient à ]0 ; +oo[.
44 :
L’espérance mathématique de vaut :
a : a.
b : 2a.
c : 3a. Vrai.
d : 4a.
L'espérance est :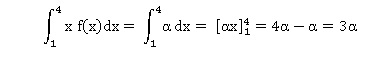
45 : La
représentation graphique de la fonction est :
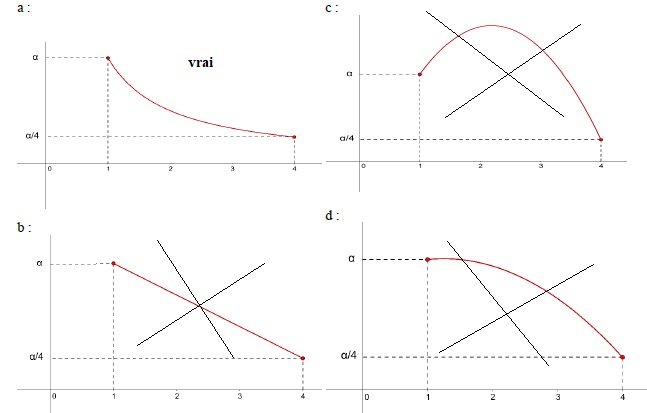
46) Le nombre a vérifie :
a : a / 4 x3 +0,5
x3 (0,75 a) <
1.
b : 0,75 ( a + 1,5a) = 1.
c : 3 a / 4. Vrai.
d : 15 a = 8.
47) P(1 < X < 2) =
a : a / 3.
b : a ln(2). Vrai.
c :a e2.
d : a / 2.
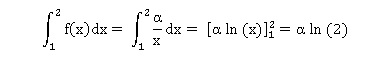
48) Le nombre a est égal à :
a : 1/3.
b : 1.
c : e4.
d: 1 / (2 ln(2)). Vrai.
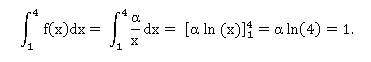
Loi normale.
49 : On considère une
variable aléatoire X qui suit une loi normale d’espérance mathématique
3 et d’écart-type 2, alors :
a : Y = (X+3) / 2 suit une loi normale centrée réduite.
b :Y = (X-3) /
2 suit une loi normale centrée réduite. Vrai.
c : Y = (X+3) / 4 suit une loi normale centrée réduite.
d : (X-3) / 4suit une loi normale centrée réduite.
50 : On
considère une variable aléatoire X qui suit une loi normale d’espérance
mathématique 2 et d’écart-type 3, alors P(X-2 < -6)~
a : 0,5.
b : 0,16.
c : 0,046.
d : 0,023. Vrai.
Algorithmique.
Pour les questions 51 à 54, on considère l’algorithme suivant :
Variables :x, y, z : nombres
Traitement :
Saisir et x, y et z
Affecter à z la valeur x
Affecter à x la valeur y
Affecter à y la valeur z
Afficher x ; y.
51 : Si on fait fonctionner l'algorithme avec x = 2, y = 1 et z = 3 , on obtient comme affichage
a : 2 ; 3
b : 3 ; 2.
c : 2 ; 1
d : Aucune des réponses précédentes n’est juste. Vrai.
Dans z on affecte 2 ; dans x on affecte 1 ; dans y on affecte 3 ; affichage : 1 ; 3.
52 : Si on fait fonctionner l'algorithme avec x =3 et y = -1, on obtient comme affichage
a : 2 ; -1.
b : -1 ; 3. Vrai.
c : -1 ; 3 ; 3
d : Aucune des réponses précédentes n’est juste.
Dans z on affecte 3 ; dans x on affecte -1 ; dans y on affecte 3 ; affichage : -1 ; 3.
53 : Avec quelles valeurs doit-on faire fonctionner l’algorithme si on désire afficher 3 ; 7 ?
a : x=2 ; y = 3 ; z = 7.
b : x=7 ; y = 3 ; z = 2. Vrai.
c : x =3 ; y = 2 ; z = 7.
d : Aucune des réponses précédentes n’est juste.
54 : Parmi les algorithmes suivants, lequel est équivalent à l’algorithme utilisé pour les questions 51 à 53 ?
a : Variables :
x ; y ; z : nombres
Traitement :
Saisir et x, y et z
Afficher x ; y
b : Variables :
x ; y ; z : nombres
Traitement :
Saisir x, y et z.
Afficher y ; z.
c : Variables :
x ; y ; z : nombres
Traitement :
Saisir x, y et z.
Afficher z ; x.
d. aucune des réponses précédentes n'est juste. Vrai. Il faudrait afficher y ; x.
Géométrie dans l'espace.
Pour les questions 55 à 60, on se place dans l'espace muni d'un repère orthonormé .
55 : On considère
la droite de représentation paramétrique x = 2-t ; y = 3+2t ; z = -1 +t
où t est réel. Une autre représentation paramétrique de d est :
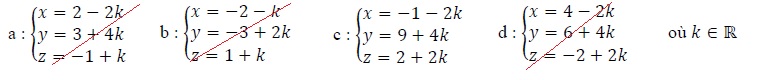
Coordonnées du vecteur directeur de la droite (d) : ( -1 ; 2 ; 1). Cette droite passe par le point A de coordonnées ( 2 ; 3 ; -1).
La proposition a: ne convient pas, les coordonnées du vecteur directeur de cette droite sont ( -2 ; 4 ; 1).
Proposition b : A appartient-il à cette droite ?
2 = -2 -k soit k = -4 ; y = -3-8 =-11 différent de 4. A n'appartient pas à cette droite.
Proposition c : coordonnées du vecteur directeur ( -2 ; 4 ; 2), c'est correct.
A appartient-il à cette droite ?
2 = -1 -2k soit k = -1,5 ; y = 9+4(-1,5) = 3 = yA ; z = 2+2(-1,5) = -1 = zA.
56. On considère le plan P d’équation cartésienne x-2y+z+1=0. L’intersection du plan P avec le plan est (O; i; j) est :
a : une droite dont le vecteur directeur est colinéaire au vecteur k .
b : une droite dont un vecteur directeur est orthogonal au vecteur k . Vrai.
c : une droite dont tous les vecteur normaux sont orthogonaux au vecteur k .
d : Aucune des réponses précédentes n’est juste.
57. On considère le plan P dont le vecteur normal a pour coordonnées ( -0,5 : 0,75 ; 0,8) et passant par le point A( 2 ; 1 ; -1).
Une équation cartésienne de P est :
a : 50 x -75 y -80z -105 = 0. Vrai.
b : -10 x +15 y +16 z +11 = 0
c : -0,5x +0,75 y +0,8z -21 / 20 = 0.
d. -20x +30 y +32 z -42 = 0.
Equation cartésienne de P : -0,5 x +0,75 y +0,8z + d = 0.
A appartient à ce plan : -0,5 x2 + 0,75 -0,8 +d = 0 ; soit d = 1,05.
58. On considère 2 points A(2 ; 0 ; 1) et B( 1 ; -1 ; 1). Une équation cartésienne du plan OAB est de la forme :
a : 7½x -7½y -14½z+d = 0 où d est réel
b : 5½x +5½y -20½z+d = 0 où d est réel
c : 11½x -11½y +44½z+d = 0 où d est réel
d : 3½x -3½y -12½z+d = 0 où d est réel. Vrai.
Equation cartésienne du plan AOB : ax +by +cz+d=0
O appartient à ce plan, donc d = 0.
A appartient à ce plan ; 2a +c = 0 soit c = -2a.
B appartient à ce plan : a -b +c = 0 ; a -b-2a = 0 soit b = -a.
59. On considère le
plan P d’équation cartésienne 2x +5y +3z+15=0. L’intersection du plan P
avec la droite passant par le point O et perpendiculaire au plan (O ; i
; k) est :
a : le point de coordonnées (0 ; -3; 0). Vrai.
b : le point de coordonnées (-7,5 ; 0 ; 0).
c : le point de coordonnées (0 ; 0 ; -5).
d : Aucune des réponses précédentes n’est juste.
Equation paramétrique de la droite : x =0; y = t ; z = 0 avec t réel.
Coordonnées du point d'intersection de cette droite et du plan P : 0 + 5t +0 +15 = 0 soit t = -3.
60. Laquelle des propositions suivantes est vraie ?
a : Il est toujours possible de trouver une droite perpendiculaire à deux plans distincts perpendiculaires entre eux.
b : Connaissant un premier plan, il est toujours possible de trouver un
autre plan tel que l’intersection des deux plans soit égale à un point
donné.
c : Connaissant 4
points distincts et alignés A, B, C, D, il est toujours possible de
trouver deux plans perpendiculaires tels que l’un des plans passe par B
et C et l’autre plan passe par A et D. Vrai.
d : Aucune des réponses précédentes n’est juste.
|
|
|