Physique,
Concours Puissance alpha 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Exercice
1. Onde progressive sinusoïdale.
Une onde périodique circulaire de fréquence f = 30 Hz est produite à la
surface d’un liquide par une pointe qui vibre de manière sinusoïdale.
Les cercles représentent les crêtes, c'est-à-dire les maxima de
vibration à une date donnée.
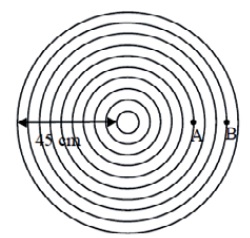
a) L’onde est transversale. Vrai.
b) La longueur d’onde � est de 15 cm. Faux.
9 crètes successives correspondent à 45 cm.
La distance entre deux crètes consécutives correspond à une
longueur d'onde. l
= 45 / 9 ~5 cm.
c) La célérité de l’onde est V = 1,5 m/s. Vrai.
V = l f = 0,05
x30 =1,5 m /s.
d) L’onde passant par A arrive en B avec un retard � t= 100 ms. Vrai.
Distance AB =
3 l = 3 x0,05 =
0,15 m.
t = AB
/ V = 0,15 / 1,5 = 0,1 s = 100 ms.
Exercice 2.Concert.
Un groupe de rock amateur comprend une guitare basse, une guitare, un
clavier, une batterie et un chanteur. À dix mètres de la scène, le
niveau sonore L, exprimé en décibel (dB), est de :
• 60 dB pour le chanteur seul
• 57 dB pour la guitare basse seule
• 60 dB pour la guitare seule
• 60 dB pour la batterie seule
• 63 dB pour le clavier seul
Données : Intensité sonore de référence I0 = 1,0 × 10−12
W.m-2 ;
log (A × B) = log A + log B ; 10 × log 2 = 3.
a) Lors du solo de guitare, l’intensité sonore est de I = 1,0 × 10−6
W.m-2. Vrai.
I = 1,0 10-12 x 106 = 1,0 × 10−6 W.m-2.
b) Le niveau
sonore du groupe lorsqu’ils jouent tous ensemble est de 300 dB. Faux.
Itotal / I0 = 106 +105,7
+106 +106 +106,3 ~5,5 106 W.m-2.
Niveau sonore du groupe 10 log(5,5 106) ~67,4 dB.
Lorsque le
chanteur et la guitare sont les seuls en action :
c) L’intensité sonore est de 1,0 × 10-3 W.m-2.
Faux.
I = 10-12( 106 + 106 )= 2,0 × 10-6 W.m-2.
d) Le niveau
sonore est de 63 dB. Vrai.
10 log ( 2 10-6 / 10-12) = 63 dB.
Exercice
3. On éclaire une fente de largeur a = 0,063 mm à l’aide d’un
laser émettant un faisceau rouge de longueur d’onde dans le vide � l= 633 nm.
Un écran est situé à une distance D = 2,0 m de la fente.
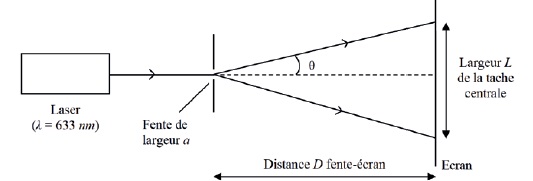
a) L’écart angulaire � de l’onde diffractée est d’environ 0,010°. Faux.
q = l / a = 633 10-9
/ 0,063 10-3 ~ 0,01 radian~0,01 x180 / 3,14 ~0,58 °.
b) La largeur de la tache centrale de diffraction sur l’écran a une
taille de 4,0 cm. Vrai.
tan q ~q= ½L / D ; L = 2D q =4 x0,01 =0,04 m = 4 cm.
c) L’écart angulaire aurait été plus grand si le faisceau laser utilisé
pour l’expérience avait été vert. Faux.
La longueur d'onde du vert est inférieure à 633 nm.
d) Si on multiplie par deux la distance entre le laser et la fente, la
largeur de la tache centrale de diffraction augmente. Faux.
Exercice 4. Effet
Doppler.
En un point O, un véhicule muni d’une sirène émet un son de fréquence f
= 1020 Hz. Le son émis se propage dans l’air à la vitesse de Vson
= 340 m.s-1. Un observateur immobile est situé au point M à
une distance d = 680 m.
Données : 1020 / 340 = 3 ; 340 / 1020 =0,33 ; 1122 / 1020 =1,10 ; 918 /
1020 = 0,90.
La fréquence fR du signal reçu dépend de la vitesse VE
et de la fréquence fE de l’émetteur selon la relation : ⨍R
= ⨍E x (1 ±VE / Vson).
Le choix du signe + ou – dans la relation dépend du rapprochement ou de
l’éloignement de l’émetteur par rapport au récepteur.
Première phase : Le véhicule est immobile
a) La longueur d’onde du son émis est � l= 3,0 m. Faux.
l =
Vson / f = 340 / 1020 = 0,33 m.
b) L’observateur perçoit le son avec un retard � t = 2,0 s. Vrai.
d / Vson = 680 / 340 = 2,0 s.
Seconde phase : Le véhicule se déplace à vitesse constante vers
l’observateur selon une droite de direction OM.
c) Le son perçu par l’observateur est plus aigu. Vrai.
d) La vitesse du véhicule est VE = 34m.s-1 pour
une fréquence perçue de 1122 Hz. Vrai.
⨍R = ⨍E x (1 +VE
/ Vson) = 1020 (1+34/340) = 1020 x1,1 = 11220Hz.
Exercice 5. Etude
documentaire : Vent solaire.
Dans l’atmosphère solaire, les collisions entre les particules sont si
violentes que les atomes d’hydrogène se décomposent en électrons et en
protons. Ce « matériel » ionisé est appelé plasma. Le vent solaire,
c’est lorsque ce plasma s’éloigne du Soleil dans toutes les directions.
La vitesse et la densité de ce vent solaire varient beaucoup ;
celles-ci sont plus grandes quand le vent provient des régions actives
du Soleil, comme les taches ou les protubérances solaires. Le vent
solaire prend un peu plus de quatre jours pour atteindre la Terre.
Lors de violentes tempêtes solaires, une grande quantité d’électrons et
de protons venant du Soleil arrivent dans l’atmosphère terrestre et
excitent les atomes d’oxygène et d’azote, lesquels deviennent
subitement lumineux et produisent les voiles de lumière colorée que
sont les aurores polaires. On les nomme polaires parce qu’une fois
arrivées dans l’atmosphère terrestre, les particules sont prises au
piège par le champ magnétique qui les
force à se diriger vers les pôles magnétiques nord (aurore boréale) et
sud (aurore australe).
D’après, E. Christian, météorologue, www.meteo.org/phenomen/aurore.htm
Données : Distance Soleil-Terre : 1,50 × 1011 m ;
Célérité des ondes électromagnétiques : 3,00 × 108 m.s-1
;
a) Le vent solaire est constitué d’électrons et de protons.Vrai.
b) Le champ magnétique terrestre a pour direction une droite
perpendiculaire à l’axe des pôles. Faux.
c) La vitesse moyenne de propagation du vent solaire est d’environ 1,6
× 106 km.h-1. Vrai.
1,50 108 / (4 x24) ~1,6 × 106 km.h-1.
d) Les ondes
électromagnétiques issues du Soleil mettent environ 5 × 101
secondes pour parvenir sur Terre. Faux.
1,50 × 1011 / (3,00 × 108) = 5 102 s.
|
|
Exercice
6.
Quantité de mouvement.
Le schéma représente le système S (supposé pseudo isolé) constitué par
un tireur, sa carabine et la balle. Lors du tir on peut décomposer le
système en deux sous-systèmes : le sous-système A {tireur + carabine}
et le sous-système B {la balle}. On note pA (respectivement pB)
la quantité
de mouvement de A (respectivement de B).
Données : mS = 80 kg ; mA = 80 kg ; mB
= 8,0 g ; vB = 3000 km.h-1 ;
24 x 36 = 8,7 x 102 ;
a) La quantité de mouvement pS de S se conserve. Vrai.
b) Après le tir, on a :
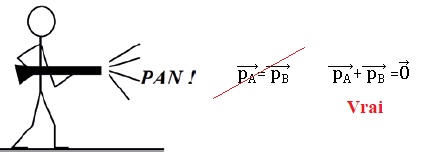
c) La valeur de pB, après le tir, est de 87 kg.m.s-1.
Faux.
mB VB = 8,0 10-3 x3000 /3,6 = 8 x 3 /
3,6 = 24 / 3,6 = 6,67 kg m s-1.
d) Le tireur est repoussé vers l’arrière avec une vitesse de 0,3 km.h-1.
Vrai.
24 / (3,6 x80) m /s ou 24 / 80 = 0,3 km.h-1.
Exercice 7. Déviation d’un
électron.
Un électron, de masse m et de charge (-e), pénètre au point O, avec une
vitesse V0 faisant un angle α = 30° avec le plan horizontal,
dans un champ électrostatique uniforme E créé par deux armatures
chargées . La vitesse d’entrée de l’électron a pour valeur V0
= 2,00 × 107 m.s-1.
Dans l’exercice, on négligera le poids devant la force électrique
exercée sur l’électron.
Données : l = 10,0 cm ; m = 9,11 × 10-31 kg ; E = 5,70 × 104
V.m-1 ; e = 1,60 × 10-19 C ;
sin(30°) =0,5 ; cos(30°) =3½/2
; tan(30°)
=” 0,57 ; 1,60 x5,70 / 9,11= 1,00.
a) Le champ électrique est perpendiculaire aux armatures et de sens
vers le bas. Faux.
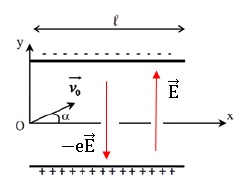
b) Les équations horaires du mouvement de l’électron sont : x = V0
t cos a ; y = eE
/ (2m) t2 + V0
t sin a ; faux.
Composantes de l'accélération : ( 0 ; -eE / m).
Composantes de la vitesse initiale ( V0
cos a ; V0
sin a ).
La vitesse est une primitive de l'accélération : ( V0
cos a ; - eE /m t
+ V0
sin a ).
La position est une primitive de la vitesse : x = V0
t cos a ; y = -
eE / (2m) t2 + V0
t sin a .
c)
L’équation de la trajectoire est y(x) = -eE / (2m) [x / ( V0
cos a)]2
+x tan a. Vrai.
t = x / ( V0
cos a) ; repport
dans y.
d) L’électron sort des plaques à l’ordonnée ysortie ”= -
0,11 m. Vrai.
y(0,1)=
-1,6 10-19 x5,7 104 / (2 x9,11 10-31)
[0,1 / (2 107 x3½/2)]2 +0,1 x0,57 =
-(1,6 x5,7 / 9,11) x 0,5 x1016
x [0,01 /
(3 1014) +0,057
= -0,5 x1016
x [1 / (3 1016)
+0,057 = -1/ 6
+0,057 ~ - 0,11 m.
Exercice 8. Chute
libre.
À un instant de date t = 0, on lance un projectile A d’un point P de
coordonnées (0;h) avec une vitesse initiale V0 , dans une
direction
qui fait un angle a
avec l’horizontale. Le point O, origine du repère, est situé au niveau
du sol. Au même instant (t = 0), on laisse tomber, sans vitesse
initiale, un projectile B d’un point I de coordonnées (xI ; hI).
On admet que les projectiles A et B sont en chute libre, le champ le
pesanteur g étant supposé uniforme.
Les projectiles A et B se rencontrent avant de toucher le sol à la date
t1.
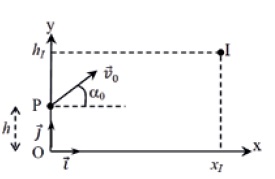
Les équations horaires sont :
Pour le projectile A : x = V0
t cos a ; y = - g
/2 t2 + V0
t sin a +h
Pour le
projectile B : xI ; - g /2 t2
+hI.
Données : v0
= 5,0 m.s-1 ; α = 45° ; h = 5,0 m ; xI = 1,0 m ;
g = 10 m.s-2 ;
2½/5= 0,28 ; sin(45°) = cos(45°) = 0,71.
a) Pour que les deux projectiles se rencontrent avant de toucher le
sol, il faut que :
xI / (V0 cos a) < (2hI / g)½
et sin(α) =(hI-h) / (V0tI). Vrai.
- g /2 t2
+ V0
t sin a +h =- g /2 t2
+hI ; V0
t1 sin a
+h =hI
; sin(α) =(hI-h)
/ (V0tI).
-g /2 t12
+hI > 0 ; xI
= V0 t1 cos a ; -g /2 [ xI
/ (V0 cos a)]2
+hI > 0 .
[ xI
/ (V0 cos a)]2
< 2hI
/ g.
b) La durée
t1 est de 0,28 s. Vrai.
t1
= xI
/ (V0 cos a)
=1 / (5 x0,71) =0,28 s.
c) Les deux
projectiles se rencontrent à l’ordonnée 5,4 m. Faux.
y = - g /2 t12
+ V0
t1 sin a
+h= -5 x0,282 +5 x0,28 x0,71 +5 = 5 x 0,28(-0,28 +0,71) +5 =
5,6 m.
d) Les
coordonnées du point I sont : xI = 1,0 m et hI =
6,0 m. Vrai.
sin(α) =(hI-h)
/ (V0tI) ; hI-h=
V0 tI
sin(α) =5 x
0,28 x 0,71 = 0,994 ;
|
|
Exercice 9.
Plan incliné.
Le wagon de queue d’un train se détache alors qu’il aborde une côte à
la vitesse v0 = 30 m.s-1. La masse du wagon et
des voyageurs est de 170 tonnes, la voie fait un angle de 10° avec
l’horizontale. Les roues du wagon sont freinées par un frottement
solide d’intensité constante F = 221 kN. Une fois immobilisé, le wagon
redescend.
Données : g × sin(10°)~ 1,7 m.s-2 ; 172 = 289 ; 4
× 17 = 68 ; 51 / 17= 3 ; 221 / 170= 1,3 ; 170 / 221~ 0,77.
Le frottement solide est présent lors de la montée et de la descente
avec la même intensité.
a) L’unité du Newton est kg.m-1.s-2. Faux.
Une force est une masse fois une accélération. kg m s-2.
b) Le wagon va s’arrêter au bout d’environ 10 secondes. Vrai.
Selon un axe
parallèle au plan incliné et orienté vers le haut la seconde loi de
Newton conduit à : a = -g sin 10 -F / m.
a = -1,7 -221 103 / (170 103) =-1,7 -1,3 = -3 m s-2.
Vitesse : v = at +v0 = -3 t +30 ; à l'arrêt t = 30 / 3 = 10
s.
c) Le travail du poids
est moteur lors de la descente. Vrai.
d) Lors de la descente, la valeur de l’accélération du wagon est de 3
m.s-2. Faux.
Selon un axe parallèle au plan incliné et orienté vers le bas, la
seconde loi de Newton conduit à : a = g sin 10 -F / m.
a = 1,7 -221 103 / (170 103) =1,7 -1,3 = 0,4 m s-2.
Exercice 10. Station
spatiale internationale.
La station spatiale internationale (ISS) est en orbite circulaire
autour de la Terre à une altitude h = 400 km. Sa vitesse est constante
et égale à V = 7,7 km.s-1. On note G la constante de
gravitation universelle.
Données : Rayon de la Terre : RT = 6,4 × 103 km ;
Masse de la terre : MT = 6,0 × 1024 kg ;
43 / 7,7= 5,6 ; 6,8 / 6,28= 1,1 ; 145 / 7,7= 19 ; 6,28 / 6,8= 0,92 ;
7,7 / 145= 0,053 ; 2 ×3,14 ’ × 6,8 = 43 ;
’ 3,14× (6,8)2 = 145 ; 43 × 7,7 = 331 ; 145 × 7,7 = 1,1 ×
103 ; 7,7 / 43= 0,18.
a) La station possède une accélération centripète a = V2 / (RT+h).
Vrai.
b) La troisième loi de Kepler s’applique en prenant l’altitude h comme
demi-grand axe de la trajectoire. Faux.
c) La troisième loi de Kepler s’écrit, dans ce cas : T3 / (RT+h)2=
4 p2
/(GMT). Vrai.
d) La période de révolution de l’ISS est T = 5,6 × 103 s. Vrai.
T = 2p (RT+h) / V = 6,28 x(6,4 103
+400 ) / 7,7 =6,28 * 6,8 x 1000 / 7,7 = 43 / 7,7 x 1000 =1000 x5,6 s.
Exercice 11. Canon
à électrons.
Soit le canon à électrons ci-dessous. Les électrons pénètrent en A
(potentiel VA) dans un champ électrostatique uniforme V qui
permet
de les accélérer et ressortent au point B (potentiel VB). On
suppose que la vitesse d’entrée au point A est quasi nulle. L’électron
n’est
soumis qu’à la force électrostatique F conservative à l’intérieur du
canon. On note d la longueur de la zone d’interaction. Lorsque
l’électron
arrive au point X (potentiel VX), sa vitesse est vX.
Données : Charge élémentaire e = 1,60 × 10-19 C ; Masse de
l’électron m = 9,11 × 10-31 kg ;
V A = - 4,55 × 103 V ; VB = 0 V ; d =
10,0 cm ; 4,55 x1,60 / 9,11= 0,800 ;
L’énergie potentielle électrique d’une charge q en un point A est Ep(A)
= qVA.
a) Le champ électrostatique a pour valeur E = 455 V.m-1.
Faux.
E =VB- VA / d = 4,55 103 / 0,10 = 4,55
104 V m-1.
b) Le travail de la force électrostatique F, lorsque l’électron se
déplace de X à B, est W = e(VX - VB). Faux.
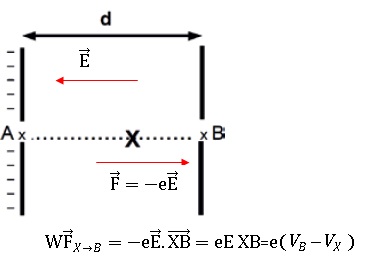
c) A une constante près, l’énergie mécanique de l’électron au point X
est E(X) =½ mv2-eVX. Vrai.
d) La vitesse au point B est vB=2,00 × 107 m.s-1.
Faux.
Variation de l'énergie cinétique entre A et B : ½ mv2-0.
Le poids étant négligeable devant la force électrique, travail de cette
force : e(VA-VB).
Théorème de l'énergie cinétique entre A et B : ½ mv2= e(VB-VA).
v2= 2e(VB-VA) / m = 2
x1,6 10-19 x 4,55 103 /(9,11 10-31)
=(4,55 x1,6 / 9,11 ) x2 x1015=16 1014 .
vB=4,00
× 107 m.s-1.
Exercice 12.
Oscillations d’un pendule.
Un pendule simple, de masse m et de longueur l, est lâché sans vitesse
initiale, d’un angle α0 = 30° (point A) avec sa position
d’équilibre. On négligera tous les frottements. L’origine des énergies
potentielles et des altitudes est prise au point B.
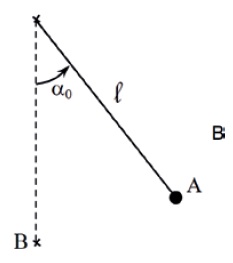
Données :l = 2,0 m ; m = 50 g ; g = 10 m s-2. cos 30 ~0,87 ;
1,3½ =1,14 ; sin 30 = 0,5.
a) L’énergie mécanique est égale à 130 J. Faux.
L'énergie mécanique se conserve et sa valeur initiale est mg l (1-cos a0) = 0,050 x10
x2,0 (1-0,87) =0,13 J.
b) Le point A est à l’altitude zA = 26 cm. Vrai.
l (1-cos a0) =2,0 (1-0,87)
= 0,26 m = 26 cm.
c) La vitesse au point B
est vB = 2,28 m.s-1. Vrai.
La conservation de
l'énergie mécanique conduit à : ½mvB2= 0,13 ; vB2=0,26
/ 0,050 =1,3 x2 / 0,5=1,3 x 4.
vB = 1,14 x2 = 2,28
m.s-1.
d) Si le pendule avait
été lâché avec une vitesse initiale de 2,0 m.s -1,
l’énergie mécanique aurait été augmentée de 100 J. Faux.
l'énergie mécanique aurait été augmentée de ½mv2 = 0,5
x0,050 x4 = 0,10 J.
Exercice 13. Voyage
spatial.
Une navette parcourt les 1300 années-lumière qui séparent la nébuleuse
d’Orion et le Soleil. Cette distance est mesurée dans le référentiel
héliocentrique. L’horloge de la navette indique que ce voyage a duré —DtN = 800 ans. Le
référentiel héliocentrique et celui de la navette sont galiléens. On
appelle D—tH
la durée du voyage dans le référentiel héliocentrique. Un contrôleur
spatial dans le système solaire observe que le voyage dure 900 ans. Les
durées propres —Dt0,
dans le référentiel Rp, et mesurées D—t, dans le référentiel R,
sont reliées par la relation : D—t
= g D—t0 où � g=1 / ( 1-v2 / c2)½
, v représente la
vitesse de Rp par rapport à R et c représente la célérité de la lumière.
Données : c = 3,00 × 108 m.s-1 ; ‹ 17½
/ 9 =0,46.
a) Le référentiel de la navette est en translation rectiligne uniforme
par rapport au référentiel héliocentrique. Vrai.
b) DtN est une durée mesurée. Faux.
c) On peut écrire D—tH
= g D—tN. Vrai.
d) La vitesse de la navette dans le référentiel héliocentrique est v ‹
=0,46c. Vrai.
g =
900 / 800 = 9 / 8
81 / 64 = 1 / ( 1-v2
/ c2) ; 1-v2
/ c2= 64 / 81 ; v2
/ c2= 17 / 81 ; v / c = 0,46.
Exercice 14.
Isolation thermique.
On estime que les maisons anciennes ont en moyenne besoin de 400 kWh
par an et par mètre carré de surface de murs, ouvertures
ou toitures pour compenser les pertes thermiques.
Dans le tableau cidessous, on donne les flux thermiques Φ ramenés à 1 m2
de surface et à 1 K de différence de températures entre l’intérieur
et l’extérieur.
Toit
|
Mur
|
Vitrage
|
Isolé
|
Non
isolé
|
Isolé |
Non
isolé |
Isolé |
Non
isolé |
0,1
W K-1 m-2
|
2,5
W K-1 m-2 |
0,1
W K-1 m-2 |
2,0
W K-1 m-2 |
2,0
W K-1 m-2 |
5,0
W K-1 m-2 |
Données : Resistance
thermique : RTH = (T1 – T2) / Φ avec T1
> T2.
a) Une maison ancienne présentant une surface totale en contact avec
l’atmosphère de 200 m2 a besoin d’une énergie d’environ 7,20
× 102 kJ pour se chauffer pendant un an. Faux.
400 x200 = 8 104 kWh ou 8 104 x 3600 = 2,88 108
kJ.
b) Pour une surface de 2,5 m2 de simple vitrage et pour un
écart de température de 10 K, le flux thermique sera de 125 W. Vrai.
5 x10 x2,5 = 125 W.
c) Pour une surface de 2,5 m2 de double vitrage et pour un
écart de température de 10 K, la résistance thermique sera de 0,50 K.W-1.
Faux.
Flux thermique : 2,0 x10 x2,5= 50 W.
RTh = 10 / 50 = 0,20 K.W-1.
d) Une bonne isolation
thermique a pour effet de diminuer le flux thermique. Vrai.
Exercice 15.
Principe du laser.
Le principe du laser réside dans l’émission stimulée des atomes
présents dans un gaz, un liquide ou un cristal. Un apport d’énergie
fait passer une grande proportion d’atomes dans un état excité Ex.
Ces atomes se désexcitent rapidement vers le premier état excité E2
appelé état métastable. Cette étape est appelée inversion de population
et elle est réalisée par pompage optique.
Considérons un atome quelconque se trouvant dans l’état d’énergie E2.
Si une radiation de fréquence �, telle que hn = E2 -E1,
rencontre cet atome, elle va provoquer sa désexcitation par émission
stimulée.
Données : La constante de Planck est h = 6,6×1034J.s ; 1 eV
= 1,60×10-19J.;
La célérité de la lumière est c = 3,00×108 m.s-1.
E1 = -10,7 eV ; E2 = -8,7 eV ; 66 x3 / 1,6 = 124
; 1,6 / (66 x3)=8 10-3.
a) Lors de l’émission stimulée, un photon identique au photon incident
est émis par l’atome. Vrai.
b) L’énergie d’un photon émis est Ephoton = 3,20×10-19
J. Vrai.
10,7 -8,7 = 2 eV ou 2
x1,6 10-19 =
3,20×10-19 J.
c) Le laser utilisé émet
un rayonnement monochromatique de longueur d’onde� l=1240 nm. Faux.
Fréquence = 3,2 10-19 / (6,6 10-34) = 3,2 / 6,6 1015
Hz.
Longueur d'onde : 3 108 x6,6 / 3,2 10-15 = 3 x 6,6 / 3,2 10-7 = (3 x66
/ 1,6) x0,5 10-8 =124 x 0,5 10-8 =620 10-9
m = 620 nm.
d) L’énergie d’un laser est concentrée dans un pinceau très étroit. Vrai.
Exercice 16.
La surface d’un disque compact (CD) comporte une piste plane avec des
alvéoles. La piste est donc constituée d’une succession de creux et de
plats. Le signal laser forme, sur le disque, une tache de diffraction
qui peut recouvrir à la fois un creux et un plat comme cela est
illustré sur le schéma cidessous.
Pour simplifier, le faisceau a été représenté parallèle. La partie du
faisceau laser réfléchie au niveau d’un plat (1) et celle réfléchie au
niveau d’un creux (2) arrivent au capteur avec un déphasage : il se
produit des interférences entre (1) et (2). Le principe du codage est
le suivant : si le faisceau atteint deux zones planes successivement ou
deux zones creuses, le nombre binaire correspondant est un 0. Par
contre si le signal passe d’un plat à un creux ou d’un creux à un plat,
le nombre binaire associé est 1. La longueur d’onde du laser est, dans
le milieu de propagation (polycarbonate), de � l= 500 nm et la profondeur
d’un creux est égale à l
/4 .Le schéma ci-dessous illustre le codage de l’information en
fonction de la succession de plats et de creux ainsi que la réflexion
du signal à une date donnée.
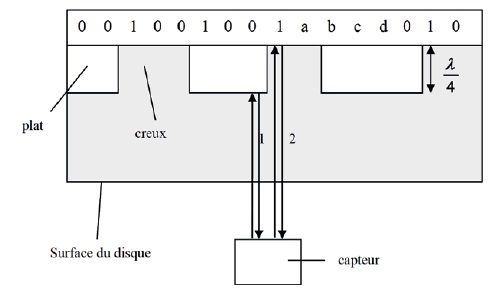
a) a = c = d = 1. Faux.
b) b = 0. Vrai.
c) La différence de marche entre 1 et 2 est de 125 nm. Faux. ( 2 x 500
/ 4)
d) Les signaux 1 et 2 interfèrent de manière destructive. Vrai.
La différence de marche est égale à 0,5 l.
|
|