Machine
de Ruhmkorff.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
L’appareil
de Ruhmkorff se compose d’une bobine isolante sur laquelle se trouvent
enroulés deux fils, l’un gros communiquant avec la pile, c’est le
circuit primaire, l’autre fin dans lequel doit circuler le courant
induit, c’est le circuit secondaire ; ce dernier atteint, dans certains
appareils, une longueur de 150 000 m et se trouve superposé à l’autre.
On obtient les courants induits en établissant dans l’inducteur des
interruptions successives.
Pour déterminer la valeur de l’inductance L1 de la bobine de
l’enroulement primaire, celle-ci est montée en série avec un
condensateur de capacité C et un conducteur ohmique de résistance R. Le
circuit ainsi constitué est alimenté par un générateur de basses
fréquences (GBF) délivrant une tension sinusoïdale.
On note e (t) = E cos (w t) la force
électromotrice du GBF et i (t) = Im cos (w t +F ) l’intensité du courant
électrique le traversant (en convention générateur). L’inductance du
circuit est L1, la capacité C et la résistance totale du
circuit Rtot.
On notera i (t) la
grandeur complexe associée à i (t) :
i (t) =Im
exp (jF)) exp (jw t) .
Q 17 Faire le
schéma électrique du circuit. Établir la relation entre e (t) et i (t) . En déduire
l’expression de l’amplitude Im de i (t) .
On note L1 = L
et Rtot =R.
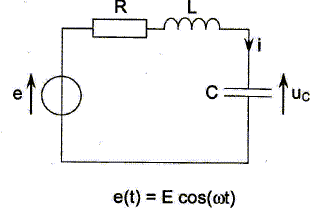
e = (R +jLw+1/(jCw) ) i ;
E exp (jw t) =(R +jLw+1/(jCw) ) Im exp (jF)) exp (jw
t).
E = (R +jLw+1/(jCw) ) Im exp (jF).
Im = Eexp
(-jF)/ (R +jLw+1/(jCw) )).
Prendre le module : Im = E / [R2 +(Lw-1/(Cw))2]½.
Q 18 Établir
l’expression de la pulsation w0 à la
résonance en amplitude de i (t) .
A la résonance, l'intensité est maximale et w = w0.
Lw0-1/(Cw0)=0 soit w0 = (LC)-½.
Q 19 Avec pour
objectif la formation d’élèves de terminale STL SPCL, proposer un
protocole expérimental permettant de déterminer la valeur de
l’inductance L1. Quelles peuvent être les sources d’erreurs
influant sur la précision de la valeur obtenue ?
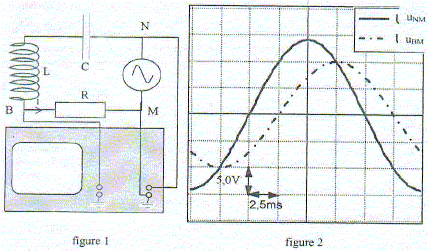
C = 1 µF et R = 10 ohms.
Faire varier la fréquence du signal délivré par le GBF. identifier la
fréquence de résonance ( courbes non décalées ).
Sachant que f résonance = 1 /(2p) (LC)½, en
déduire la valeur de L.
Sources d'imprécision : précision sur la capacité C du condensateur et
précision sur la mesure de la fréquence.
|
...
|
|
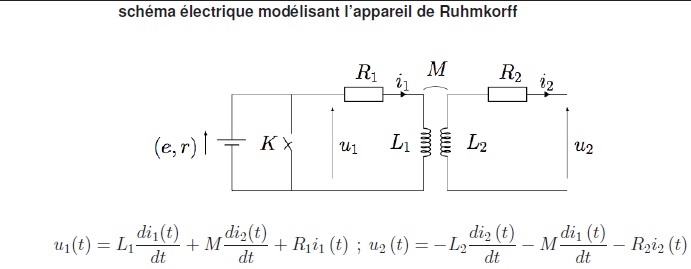
Une pile au bichromate de potassium délivre une
tension continue
de valeur 2 V; elle est modélisée par l’association série d’une source
idéale de tension de force électromotrice e et d’un résistor de
résistance r.
Pour ioniser le gaz à l’intérieur de la lanterne, une tension de
plusieurs milliers de volts peut être nécessaire. Pour générer une
telle tension, on utilise un appareil de Ruhmkorff qui est un
transformateur élévateur de tension. Le transformateur est caractérisé
par ses coefficients d’inductances, L1 est l’inductance
propre du primaire, L2 celle du secondaire et M est le
coefficient d’inductance mutuelle avec |M| < (L1L2)½.
La tension u2 est appliquée aux bornes de la lanterne.
Dans un premier temps la lanterne est éteinte, donc i2 (t) =
0 A, et l’interrupteur K est ouvert.
Q 20 La tension u1
(t) possédant la valeur U0 depuis longtemps, on ferme
l’interrupteur K à l’instant t = 0,
u1 passe alors instantanément de U0 à 0 V.
Déterminer l’expression de i1 (t) pour t > 0.
u1(t) = 0 ; Ldi1(t) / dt +R1i1(t)
= 0.
i1(t) = A exp(-R1 / L1 t) avec A une
constante.
La continuité de i1 à l'instant t =0 conduit à : i1(t=0-)
= i1(t=0+) ; A = U0 / R1.
i1(t) = U0 / R1
exp(-R1 / L1 t).
Q 21
Déterminer l’expression de u2 (t) pour t > 0 et montrer
que la relation donnant la valeur maximale |U2| de u2
(t) est : |U2| = MU0 / L1.
À quel instant est-elle obtenue ?
i2(0) = 0 ; u2(t) =
-Mdi1(t) / dt=MU0 / L1exp(-R1
/ L1 t).
u2 max = u2(t=0) = MU0
/ L1.
Q 22
À quelle condition sur u2 (t) la lanterne s’allume-t-elle ?
En déduire la nécessité d’interruptions successives à l’aide de
l’interrupteur K.
Le gaz contenu dans la lanterne est ionisé si la tension u2
atteint une valeur importante.
A la fermeture de l'interrupteur K, u2 prend une valeur
importante puis décroït rapidement.
Il faut donc alternativement ouvir puis fermer K afin de faire croître u2.
|
....
|
Q 23
On suppose que la lanterne contient du diazote sous faible pression
(quelques Pa). À l’aide des documents proposés dans cette partie,
estimer la valeur de l’inductance L2 de la bobine du circuit
secondaire nécessaire à l’allumage de cette lanterne. On prendra L1
= 5 mH. Commenter l’ordre de grandeur de la valeur de l’inductance L2
trouvée.
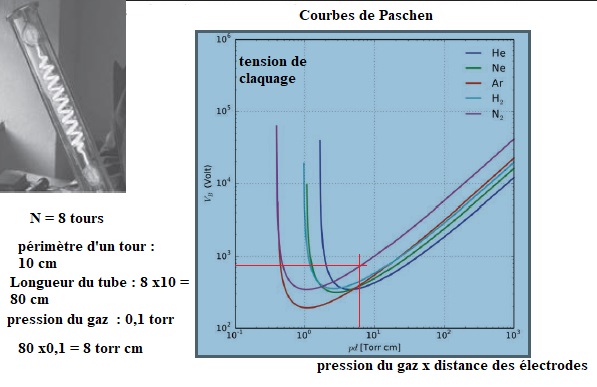
La tension de claquage est d'environ 900 V.
u2 max = 900 = MU0
/ L1; M = 900 L1 / U0 = 900 x5 10-3 /
2 = 2,25.
Pour un couplage parfait : M = (L1L2)½
; L2 = M2 / L1 = 2,252 / (5
10-3) ~1000 H.
Cette valeur étant très élevée, la bobine du secondaire doit comporter
un grand nombre de spires.
|
|



