Mathématiques, Nombres complexes, concours ENSM

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.



. .
.
.


2016 .
Question 4 ( 5 points). Vrai ou faux avec justification.
1. Le plan complexe est muni d'un repère orthonormé direct. Pour tout n entier naturel, Mn désigne le point de ce plan dont l'affixe est définie par :
z0 = 1 et zn+1 =(1-i 3½) zn.
Affirmation 1 : Le triangle OMnMn+1 est un triangle rectangle. Vrai.
z1 =1-i 3½ , M1( 1 ; -3½) ; OM12 = (1+(-3½)2) = 4.
z2 =(1-i 3½ )2= -2 -2i 3½ ; M2( -2 ; -2 *3½) ; OM22 = (4+(-2*3½)2) = 16 ;
M1M2 2=( (-2-1)2 +(-2 *3½+3½)2)½ =12.
Angle formé entre OMn et OMn+1 : 60 °.
OMn+1 / OMn = 2. le triangle OMnMn+1 est un triangle demi-équilatéral.

Affirmation 2 : Il n'existe aucune valeur de n pour laquelle Mn est un point de l'axe vertical. Vrai.
On pose y =1-i 3½  ; |y| = (1 +3)½ = 2 ; y / |y| =0,5 -i 3½ / 2 = e-ip/3.
zn+1 =2e-ip/3zn = 2n+1 exp (- i(n+1)p /3) =2n+1 ( cos ( (n+1)p /3))-i sin( (n+1)p /3))).
zn+1 est un imaginaire pur si (n+1)p /3) =k p /2 avec k entier ; (n+1) / 3 = k / 2 ; n+1 = 1,5 k ; n = 1,5 k-1.

2015.

On se place e dans le plan complexe  et on considère pour tout nombre α appartenant à C, le point Ma d'affixe a2-a.

1. On considère les points Ma et Ma+3.
(a) Montrer que O est le milieu de [MaMa+3] lorsque a2+2a+ 3 = 0.
Ma d'affixe a2-a ; Ma+3 d'affixe (a+3)2-a-3 ; O d'affixe 0.
a2-a +(a+3)2-a-3 =0 ;
a2-a +a2+6a+9-a-3 =0 ; 2a2 +4a+6 =0.
(b) En déduire les valeurs de α pour lesquelles O est le milieu de [MaMa+3]
Discriminant D = 22-4x3=-8 = 8 i2.
Solutions : (-2 ±2i *2½) / 2 = -1±i *2½.
 2. Montrer que lorsque |α −½| = 2 alors Ma est sur un cercle de rayon 4 et de centre W d'affixe −1/4.
(a-½)2 = 4 ; a2-a+1/4 = 4.
Il existe un point W ( 0 ; -1/4) tel que :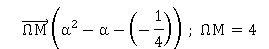
3. On suppose ici qu'il existe θ appartenant à [−π; 0] tel que α = eiq.
(a) Montrer que α2 − α = 2 sin(θ/2) exp[i(3q+p)/2]

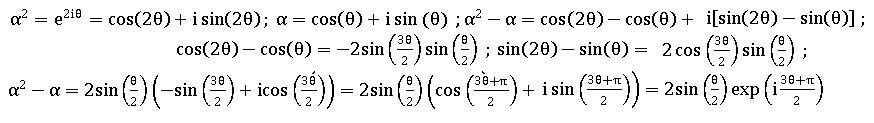
(b) En déduire un argument de α2 − α en fonction de θ.
(3q+p) / 2.
.

2013.
Le plan complexe est muni d'un repère orthonormé direct. q désigne un élément de l'intervalle ]- p/2 ; p/2 [.
On note z0 le nombre complexe défini par : z0 = 1 +exp(2iq).
1. Une écriture exponentielle de z0 est z0 = 2 cos (q) exp(iq). Vrai.
z0 = 1 +cos(2q) +i sin (2q).
| z0 |2 =(1 +cos(2q) )2+sin2 (2q)= 2+2cos(2q) = 4cos2(q) ; |z0|= 2 cos (q).
z0 / |z0|= cos a + i sin a = (1 +cos(2q)) / (2 cos (q)) +i sin (2q) /(2 cos (q)).
On identifie : cos a = (1 +cos(2q)) / (2 cos (q)) = cos(q) ;
sin (2q) /(2 cos (q)) = 2 sin(q) cos (q) / (2 cos (q)) = sin (q).

2. Si q = p/6, z02013  est un nombre réel. Faux.
[2 cos (p/6)]2013 exp(i 2013p /6) ;
2013p /6 =335,5 p =167 x(2p) +1,5 p.

 3. z0 = 4 /z0 si et seulement si q = 2kp avec k appartenant à Z. Faux.
z0 = ±2 ; 2 cos (q) exp(iq) = ± 2 ; cos (q) exp(iq) = ± 1.
cos (q) (cos (q) +i sin (q)) = ±1 ; sin (q) = 0 ; q = k p.





2017
1. On considère le polynôme P défini sur C par : P(z) = z3 +(2+2i)z2 +(4-4i)z -8i.
1.1. Démontrer que 2i est une solution de l'équation P(z) = 0.
P(2i) = (2i)3+(2-2i)(2i)2 +(4-4i)(2i) -8i.
P(2i) = -8 i -4(2-2i) +(4-4i)(2i) -8i.
P(2i) = -16 i-8 +8i +8i+8 = 0.
1.2. Démontrer que P(z) = (z-2i)(z2+2z+4).
P(z) = (z-2i)(z2 +az +b).
On développe : P(z) = z3 +az2 +bz -2iz2-2aiz-2ib.
P(z) =z3 +(a-2i)z2 +(b-2ai)z-2ib= z3 +(2+2i)z2 +(4-4i)z -8i.
On identifie : a = 2 ; b = 4.
1.3. En déduire toutes les solutions dans C de l'équation P(z) = 0.
z2+2z+4 = 0 ; discriminant  D = 4-16 = -12 = 12 i2.
z1 = (-2 +2*3½i) / 2 = -1 +3½ i.
z2 = (-2 -2*3½i) / 2 = -1 -3½ i.
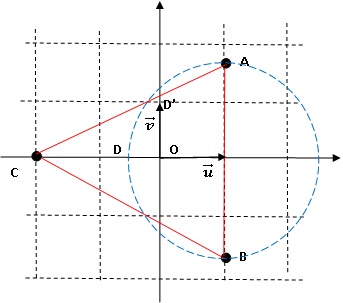
2. On considère les points A, B et C d'affixes respectives : zA =1+i3½ ; zB = 1-i 3½ et zC = -2.
2.1. Déterminer le module et l'argument de ces nombres puis les écrire sous forme exponentielle.
|zA| = (1+3)½ = 2 ; zA / |zA|=1 / 2 +i 3½ / 2 = cos (p/3) + i sin (p/3) ; zA = 2 exp(ip/3).
|zB| = (1+3)½ = 2 ; zB / |zB|=1 / 2 -i 3½ / 2 = cos (-p/3) + i sin (-p/3) ; zB = 2 exp(-ip/3).
|zC| = 2 ; zC = 2 exp(ip).
2.2. Placer les points sur une figure que l'on complètera au fur et à mesure de l'exercice.

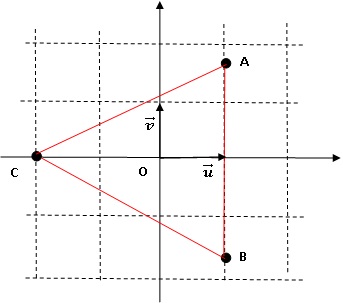
2.3. On note Z =( zA-zC) / (zB-zC). Déterminer la forme algébrique de Z ; calculer son module et son argument et en déduire la nature du triangle ABC.
zA-zC= 3 +i3½ ; zB-zC= 3 -i3½.
Z = (3+i3½)  / (3-i3½)= (3+i3½)2  / (9 +3)=(9+3+6 i 3½) / 12 =0,5(1+ i 3½) = cos (p/3) + i sin (p/3) ;
|Z|=0,5(1+3)½ =1 ; Z =  exp(ip/3).
Le triangle ABC est équilatéral.
3. A tout point M d'affixe z= a+ib ( avec z différent de zB), on associe le point M' d'affixe z' = (1+i 3½-z) / (1-i 3½-z)= (zA-z) / (zB-z).
3.1. Démontrer que si le point M appartient à la médiatrice du segment [AB] alors M' appartient à un cercle dont on précisera le centre et le rayon.
M est sur la médiatrice de [AB] ; M appartient à l'axe horizontal des nombres réels : affixe de M ; z = a.
MA=MB ; |zA-z| = |zB-z|. Le module de z' est égal à 1.
zA-z = (1-a)+i3½ ; zB-z = (1-a)-i3½ ;
  |zA-z| =((1-a)2 +3]½ ; |zB-z| =((1-a)2 +3]½ ;
z' =  [(1-a)+i3½] /  [(1-a)-i3½] = [(1-a)+i3½]2 / [(1-a)2 +3] = [(1-a)2-3 +2i(1-a)3½] / [(1-a)2 +3] = x+i y. 
On identifie partie réelle et partie imaginaire :
 x=(1-a)2-3) /[(1-a)2 +3] ; y =2(1-a)3½ / [(1-a)2 +3].
 x2 +y2 =1
M' appartient au cercle de centre (0 ; 0) et de rayon 1.

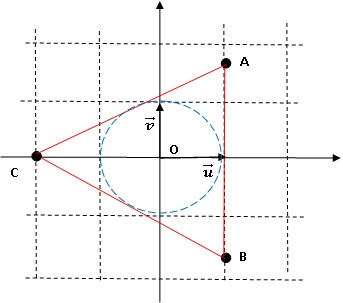3.2. Démontrer que si M appartient au cercle de diamètre [AB] privé de B, alors M' appartient  à l'axe vertical.
M est tel que (x-1)2 + y2 = 3 avec z = x+iy
zA-z = (1-x)+i(3½-y) ; zB-z = (1-x)-i(3½+y) ;  z' =[(1-x)+i(3½-y)] / [(1-x)-i(3½ +y)] =[(1-x)+i(3½-y)] [(1-x)+i(3½ +y) ]/ [(1-x)2+(3½ +y)2] .
z'  = [(1-x)2-(3-y2)+2i(1-x)(3½)]/ [(1-x)2+(3½ +y)2] ;
z' =2i(1-x)(3½)] / [(1-x)2+(3½ +y)2] ; z' est un imaginaire pur.

3.3. On note D le point d'intersection entre le cercle de diamètre AB et l'axe réel, tel que DBA soit un triangle rectangle direct. Construire le point D' associé à D en justifiant la construction.
xD = - 3½+1 ; yD = 0 ;  1-x = 3½ ; z' = 6i /(3+3)= i.