Mathématiques,
Bac ST2S métropole 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Exercice
1. Partie A.
Le taux d'emploi des personnes handicapées dans la fonction publique progresse fortement depuis 2010.
Année
|
2010
|
2011
|
2012
|
2013
|
2014
|
2015
|
Rang de l'année ( xi)
|
0
|
1
|
2
|
3
|
4
|
5
|
Part des salariés handicapés ( yi) %
|
3,98
|
4,22
|
4,39
|
4,64
|
4,9
|
5,17
|
1. Déterminer les coordonnées ( xG et yG) du point moyen de ce nuage de points. Placer ce point sur le graphe.
xG = (0 +1 +2 +3 +4 +5) / 6 = 2,5.
yG=(3,98 +4,22 + 4,39 +4,64 +4,9 +5,17) / 6 =4,55.
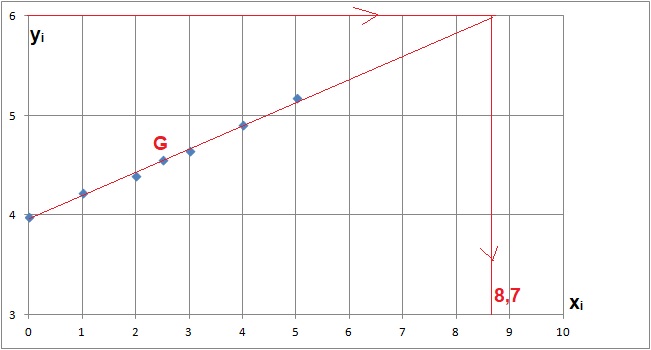
2. On peut envisager d'eefectuer un ajustement affine. la droite d'ajustement a pour équation y = 0,24x +3,95.
a. Justifier que le point G appartient à cette droite.
y = 0,24 x 2,5 +3,95 = 4,55 = yG.
b. Construire cette droite en précisant les coordonnées des points utilisés.
On utilise le point G et par exemple le point( 0 ; 3,95).
3. On utilise cet
ajustement pour effectuer des prévisions au-delà de 2015. A partir de
quelle année, peut-on estimer que la part des salariés handicapés
atteindra 6 % ?.
6 = 0,24 x +3,95 ; x = (6-3,95) / 0,24 = 8,54 ; année 2019.
Partie B.
Le tableau ci-dessous donne, de 2015 à 2017, le nombre total de
salariés ainsi que le nombre de salariés handicapés d'une entreprise
privée.
Année
|
2015
|
2016
|
2017
|
Nombre total salariés
|
1764
|
1771
|
1805
|
Nombre de salariés handicapés
|
60
|
62
|
65
|
1. Calculer à 0
2.2. Citer le n,1 % près le taux dévolution de 2016 à 2017 du nombre de salariés handicapés.
(65-62) / 62 x 100 ~4,8 %.
A partir de 2017, le nombre de salariés handicapés augmente de 5 % chaque année et on modélise cette évolution par une suite.
u0 = 65.
2. Indiquer sanns justification la nature de cette suite. Donner sa raison.
C'est une suite géométrique de raison 1,05.
3. On utilise un
tableur pour obtenir les termes de la suite. Quelle formule peut-on
saisir dans la cellule C2 qui, recopier vers la droite, permet de
remplir ce tableau ?
|
A
|
B
|
C
|
D
|
E
|
1
|
Année
|
2017
|
2018
|
2019
|
2020
|
2
|
Nombre de salariés handicapés |
65
|
=1,05*B2
|
|
|
4 Etude de la suite (un).
a. Exprimer un en fonction de n.
un = 65 x 1,05n.
b. Calculer u3 ( arrondir à l'unité). Interpréter ce résultat.
u3 = 65 x1,053 =75,24 ~75.
En 2020, il y aura 75 salariés handicapés.
5. Selon ce modèle,
sachant que l'entreprise s'est fixé comme perspective d'employer 1850
salariés en 2020, peut-on penser que la part des salariès handicapés
atteindra 6 % en 2020 ?
1850 x 6 / 100 = 111.
Le modèle conduit à 75, valeur inférieure à 111. La part des salariès handicapés n'atteindra pas 6 % en 2020 ?
|
|
|
|
|
Exercice 2.
Taille de l'échantillon : 1000.
9 % des personnes sont atteintes de maladies cardio-vasculaires.
Parmi ces personnes, 45 % pratiquent une activité physique régulière.
Parmi les personnes non atteintes d'une maladie cardio-vasculaire, 60 % pratiquent une activité physique régulière.
On choisit une personne au hasard dans l'achantillon et on note :
M l'événement " la personne est atteinte d'une maladie cardio-vasculaire".
S l'événement " la personne pratique une activité physique".
1. Un arbre de probabilité.
a. Donner P(M) et PM(S).
P(M) = 0,09 ; PM(S) =0,45
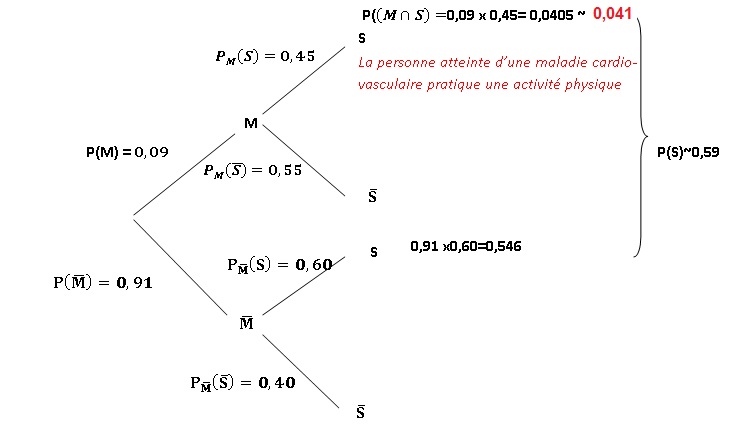
b. Recopier et compléter l'arbre de probabilités suivant.
2. a. calculer P(M n S) et interpréter.
2.b. Montrer que la probabilité, que la personne pratique une actovité physique régulière est 0,59.
3.
Sachant que la personne pratique une activité physique régulière,
quelle est la probabilité qu'elle soit atteinte d'une maladie
cardio-vasculaire ?
PS(M) = P(S n M) / P(S) = 0,041 / 0,59 = 0,069~0,07.
4. Montrer que Pnon S (M) = 0,12.
P(non S) = 1-0,59 = 0,41.
Pnon S (M) =P(non S n M) / P(non S) = 0,55 x0,09 / 0,41 = 0,12.
5.
Une campagne de sensibilisation affirme qu'une activité physique
régulière fait baisser de plus de 30 % la probabilité d'être atteint
d'une maladie cardio-vasculaire. Que pensez-vous de cette affirmation ?
(0,07 -0,12) / 0,12 = -0,42. L'affirmation est vraie.
|
|
.Exercice 3. Partie A.
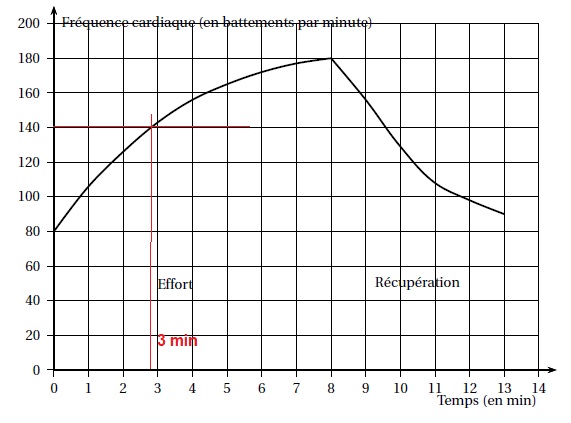
Le
graphique ci-dessous représente l'évolution de la fréquence cardiaque
d'un homme de 40 ans en fonction du temps, pendant un effort physique
puis pendant la phase de récupération.
1. Pendant la phase d'effort, au bout de combien de minutes la fréquence cardiaque dépasse t-elle 140 battements par minute ?
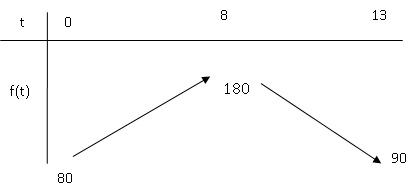
2. Tracer le tableau de variation de la fonction f définie sur [0 ; 13 ] et représentée ci-dessus.
3. Quelle est la fréquence cardiaque maximale atteinte ?
180.
Partie B.
Pour un individu A, on enregistre la fréquence cardiaque pendant la
phase de récupération après un test d'effort. Cette fréquence peut être
modémisée par la fonction g définie sur [8 ; 13] par g(t) = 660 x0,85t.
1. Justifier que la fonction g est décroissante.
0 < 0,85 < 1, la fonction g est donc décroissante.
2. Compléter le tableau de valeurs suivant :
t
|
8
|
8,5
|
9
|
9,5
|
10
|
11
|
12
|
13
|
g(t)
|
180
|
166
|
153
|
141
|
130
|
110
|
94
|
80
|
3. Compléter le graphique en traçant la courbe C1 représentative de la fonction g. 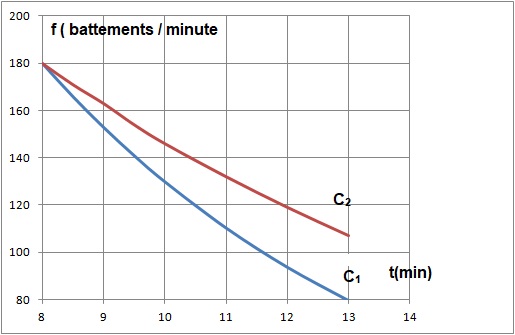
4.a. Résoudre dans l'intervalle [8 ; 13], l'inéquation 660 x0,85t <115.
En déduire le temps de récupération à partiir duquel la fréquence
cardiaque est inférieuure à 115 battements / minute.
ln (660 ) + t ln(0,85) < ln(115).
t < ( ln (115) - ln(660) ) / ln (0,85 ;
t < -1,747 / (-0,1625) ; t > 10,75.
10,75 - 8 = 2,75 min ou 2 min 45 s.
Une diminution de fréquence cardiaque infériieuure à 12 battements lors
de la première minute de récupération est considérée comme anormale.
5. La fréquence cardiaque de récupération de l'individu A peut -elle être considérée comme anormale.
g(8) = 180 ; g(9) = 153 ; 180 -153 = 27, valeur supérieure à 12.
La fréquence cardiaque de récupération de l'individu A est normale.
6. La courbe C2
représente l'évolution de la fréquence cardiaque d'un individu B ayant
été soumis au même test d'effort que l'individu A. Quel individu
présente la récupération cardiaque la plus efficace ? Justifier.
La rapidité de récupération cardiaque est un indice important de bonne forme. A est en meilleure forme que B.
|
|