Mathématiques,
Bac ST2S Polynésie 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Exercice
1.
Un établissement compte 800 élèves dont 40 % sont des garçons. 35 % des élèves sont des fumeurs ; 224 garçons ne fument pas.
Partie A.
Compléter le tableau.
L'élève est
|
un garçon
|
une fille
|
Total
|
Fumeur
|
280-184=96
|
480-296=184
|
800 x0,35=280
|
Non fumeur
|
224
|
520-224=296
|
800-280=520
|
Total
|
800 x0,40 =320
|
800-320 =480
|
800
|
Partie B.
On choisit au hasard un élève de l'établissement. On considère les événements suivants :
G " l'élève est un garçon".
A " l'élève est fumeur".
1. Montrer que la probabilité de l'événement G n non A est 0,28.
Probabilité qu'un garçon soit non fumeur : 224 / 800 = 0,28.
2. Calculer la probabilité de l'événement " l'élève est une fillle fumeuse".
184 / 800 = 0,355 ~0,36.
.3. Sachant que l'élève choisi est fumeur, quelle est la probabilité que ce soit une fille ?
184 / 280 ~0,66.
4. L'élève choisi est un garçon. y-a-t-il plus de chance que ce soit un élève fumeur ou non-fumeur ?
Probabilité qu'un garçon soit non fumeur : 224 / 320 =0,70.
Probabilité qu'un garçon soit fumeur : 96 / 320 = 0,30.
Le garçon choisi a plus de chance d'être non fumeur.
Exercice 2.
|
A
|
B
|
C
|
D
|
E
| F
|
G
|
H
|
I
|
1
|
Année de naissance
|
1980
|
1985
|
1990
|
1995
| 2000
|
2005
|
2010
|
2015
|
2
|
Rang de l'année ( xi)
|
0
|
5
|
10
|
15
| 20
|
25
|
30
|
35
|
3
|
Espérance de vie ( yi)
|
74,1
|
75,3
|
76,6
|
77,8
|
79,1
|
80,2
|
81,7
|
82,7
|
4
|
Taux d'évolution par rapport à
l'espérance de vie en 1980 ( %)
|
|
1,6
|
3,4
|
5,0
|
6,7
|
8,2
|
10,3
|
|
Les cellules de la ligne 4 sont au format pourcentage.
Partie A.
1. Quel est, en pourcentage, le taux d'augmentation de l'espérance de vie entre 1980 et 2015 ?
(82,7-74,1) / 74,1 x100 =11,6 %.
2..Parmi les
formules ci-dessous, quelle est celle qui, saisie dans la cellule C4 et
recopiée vers la droite, permet de compléter la ligne 4 ?
=(C3-B3) / B3 ; =(C3-$B3) /$B3 ( exact) ; =($C3-B3) / B3 ; =(C3-B3) / $B3.
Partie B.
1. Calculer les coordonnées du point G moyen et le placer danns le repère.
xG = (0 +5 +10 +15 +20 +25 +30 +35) / 8 =17,5.
yG = (74,1 +75,3+76,6+77,8+79,1+80,2+81,7+82,7) / 8 =78,4375 ~78,4.
2 On décide d'ajuster ce nuage de points par la droite D d'équation y = 0,24 x+74,1
a. Tracer la droite D en indiquant les points utilisés.
Point G et point de coordonnées ( 0 , 74,1).
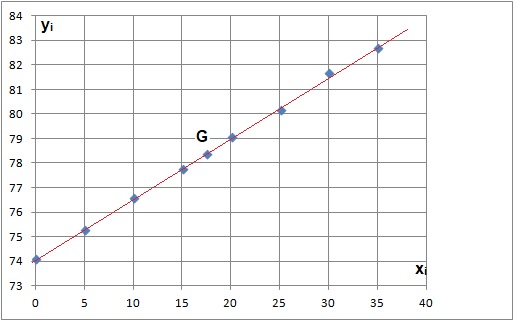
b. Donner une estimation de l'espérance de vie en 2020.
x = 40 ; y = 0,24 x40 +74,1 = 83,7.
c. Sur la base de ce modèle, à partir de quelle année l'espérance de vie dépassera-t-elle 83 ans ?
0,24 x +74,1 > 83.
0,24 x >83-74,1 ;
x >37 ; ( année 1980 +37 =2017 ).
|
|
|
|
|
Exercice 3.
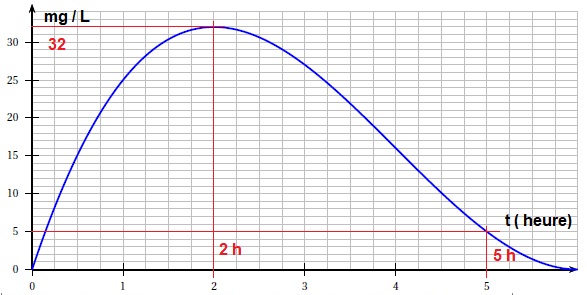
La concentration ( mg / L) du produit actif d'un médicament dans le sang est modélisé par une fonction f( t) avec t en heure.
Etude graphique.
1. Au bout de combien de temps la concentration du produit est-elle maximale ? Estimer cette concentration maximale.
2. Le
produit actif est efficace si sa concentration dans le sang est
supérieure à 5 mg / L. Au bout de combien de temps faut-il administrer
le médicament pour maintenir son effet ?
Etude de la fonction.
La fonction f est définie sur [0 ; 6 ] par f(x) = x3-12x2+36x.
1.a. Calculer la dérivée f '(x).
f '(x) = 3 x2 -24x +36.
b. Vérifier que f '(x) = (3x-6) ( x-6).
(3x-6) ( x-6) = 3x2 -18x -6x +36 = 3 x2 -24x +36.
2. Etudier le signe de f '(x) et en déduire le tableau de variations de f.
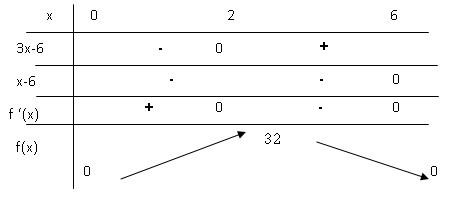
|
|
1. La réponse à la question 1 partie A eest-elle confirmée ?
Oui, la concentration maximale ( 32 mg / L) est atteinte au bout de 2 heures.
2.
L'affirmation " au bout de 5 h, la concentration dans le sang est
inférieure à 20 % de sa valeur maximale " est-elle vraie ?
Justifier par un calcul.
32 x0,20 =6,4 mg /L.
f(5) = 53-12x52+36x5 =125-300+180 = 5.
5 est inférieure à 6,4. l'affirmation est confirmée.
|
|