Mathématiques,
Bac ST2S Antilles 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Exercice
1.
En 2014, en France, 37 % des prélèvements sont été effectués sur des eaux minérales. Parmi eux 96,5 % étaient conformes.
61 % ont été effectués sur des eaux de sources. Parmi eux, 99,4 %
étaient conformes. parmi les rélèvements d'eaux rendues potables par
traitements, 96,1 % étaient conformes.
On choisit un prélèvement au hasard dans l'ensemble des prélèvements. On considère les événements suivants :
M : " le prélèvement a été effectué sur une eau minérale".
S : " le prélèvement a été effectué sur une eau de source".
R : " le prélèvement a été effectué sur une eau rendue potable par traitement".
C: " le prélèvement est conforme".
1.a. Déterminer la probabilité de l'évènement S.
0,61.
1.b. Calculer la
probabilité que le prélèvement soit non conforme sachant qu'il a été effectué sur une eau minérale.
PM(non C) = 1-0,965 = 0,035.
2. Compléter l'arbre de probabilité.
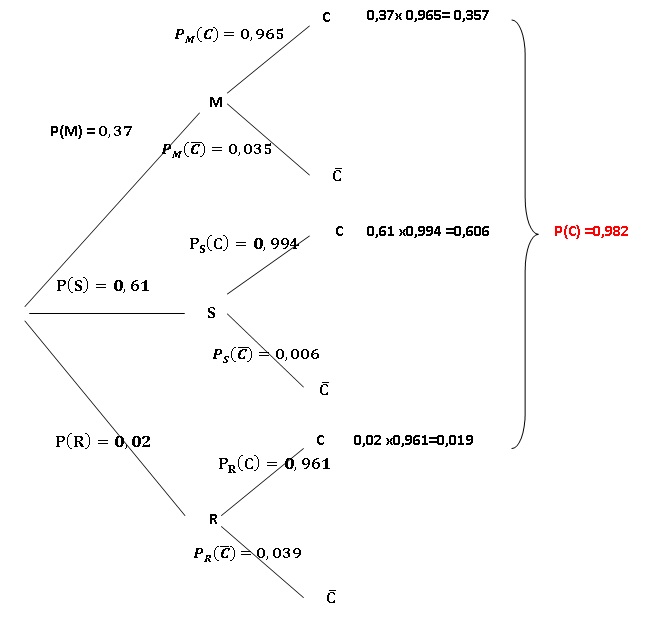
3.a. Décriire par une phrase l'évènement M n C et calculer sa probabilité.
Le prélèvement a été effectué sur une eau minérale et il est conforme.
0,37 x 0,965 = 0,357.
3.b.
Montrer que la probabilité que l'évènement choisi soit conforme et ait
été réalisé sur une eau rendue potable par traitement est d'environ
0,019.
0,02 x0,961 = 0,019.
4. Montrer que la probabilité que le prélèvement choisi soit conforme est d'environ 0,982.
0,37 x 0,965 + 0,61 x 0,994 + 0,02 x 0,961 = 0,982.
5. On choisit un
prélèvement au hasard parmi les prélèvements non conformes. Calculer la
probabilité que le prélèvement ait été effectué sur une eau minérale.
P(non C) = 1-0,982 = 0,018 ; P(M n non C) = 0,37 x 0,035 = 0,013 ; 0,013 / 0,018 = 0,72.
|
|
|
|
|
Exercice 2. Partie A.
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
| J
|
K
|
1
|
Année
|
2006
|
2007
|
2008
|
2009
|
2010
|
2011
|
2012
|
2013
| 2014
|
2015
|
2
|
Dépenses en milliers d'euros
|
1462
|
1584
|
1718
|
1834
|
1950
|
2028
|
2106
|
2182
| 2257
|
2339
|
3
|
Taux d'évolution entre deux années consécutives %
|
|
8,3
|
|
|
|
|
|
|
|
|
Les
cellules de la ligne 3 sont au format pourcentage.
1. Calculer le taux d'évolution, en %, des dépenses entre 2006 et 2015.
(2339 - 1462) / 1462 x100 = 59,986 ~60 %.
2..Quelle formule, saisie dans la cellule C3 et
recopiée vers la droite, permet de compléter la ligne 3 ?
=(C2-B2)/B2
Partie B
Année
|
2006
|
2007
|
2008
|
2009
|
2010
|
2011
|
2012
|
2013
| 2014
|
2015
|
rang de l'année xi
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
| 8
|
9
|
Dépenses en milliers d'euros yi
|
1462
|
1584
|
1718
|
1834
|
1950
|
2028
|
2106
|
2182
| 2257
|
2339
|
1. Calculer les
coordonnées du point G moyen et le placer dans le repère.
xG
= (0 +1 +2 +3 +4 +5 +6 +7 +8 +9) / 10 =4,5.
yG = (1462 +1584 +1718 +1464 +1950 +2028 +2106 +2182 +2257 +2339) / 10
=1946.
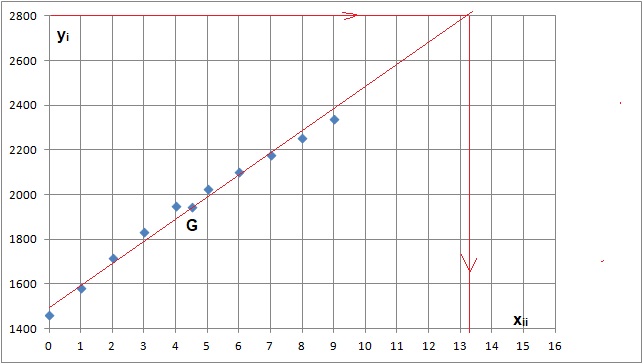
2 On décide
d'ajuster ce nuage de points par la droite D de coefficient directeur 96
a. Montrer que l'équation réduite de la droite est y = 96 x +1514.
Le point G appartient à cette droite.
1946 = 96 x 4,5 +b ; b = 1514.
b. Déterminer par le calcul une prévision des dépenses en 2018.
x = 12 ; y = 96 x12 +1514 = 2666.
c. Tracer la droite
D en indiquant les points utilisés.
Point G et point de coordonnées ( 0 , 1514).
d. Déterminer par lecture graphique, l'année à partir de laquelle les dépenses dépasseront 2,8 milliards d'euros.
x =13,3 ( 14) ; (
année 2006+14 =2020 ).
|
|
Exercice 3. Partie A.
On note f la fonction qui au temps ( ms) associe la pression artérielle
radiale ( mm Hg), mesurée au repos chez un patient suspecté
d'insuffisance cardiaque. On considère C la courbe représentative de f
sur l'intervalle [0 ; 650 ].
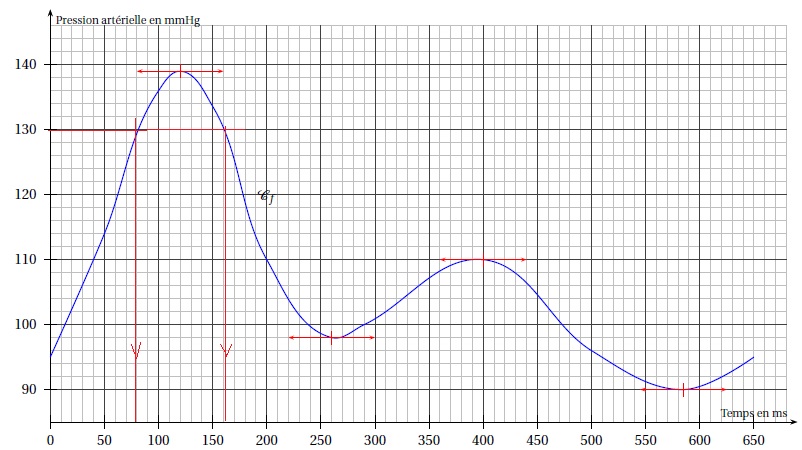
1. Dresser le tableau de variation f.
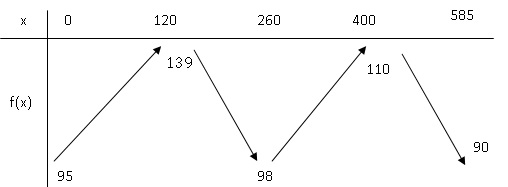
2. Sur quel intervalle de temps la pression est-elle supérieure à 130 mm Hg ?
[ 80 ; 160 ms ].
3.a. Déterminer la valeur systolique ( valeur maximale) et la valeur diastolique ( valeur minimale ) de la pression artérielle.
Maxi : 139 mm Hg ; mini : 90 mm Hg.
3.b. Un patient est
en hypertension artérielle lorsque la pression systolique est
supérieure ou égale à 140 mm Hg ou que la pression diastolique est
supérieure ou égale 90 mm Hg. Ce patient est-il en hypertension ?
Justifier.
Oui, la valeur minimale de la pression est égale à 90 mm Hg.
3.c La valeur 650
ms correspond à celle d'un battement de coeur du patient. On parle de
tachycardie lorsque au repos, le nombre de battements de coeur est
qupérieur à 100 par minute. peut-on estimer que le patient souffre de
tachycardie ?
650 ms = 0,65 s.
Nombre de battements par minute : 60 / 0,65 ~92, valeur inférieure à100. Non le patient ne souffre pas de tachucardie.
Partie B. Scintigraphie cardiiaque.
On injecte au patient un échantillon de thallium d'activité 60 MBq. A
chaque demi-vie radioactive, l'activité initiale est divisée par deux.
On note u0 l'activité initiale et un l'activité après n demi-vie.
1. Calculer u0, u1, u2 et u3.
u0 = 60; u1 =30 ; u2 = 15 ; u3 = 7,5.
2. Exprimer un+1 en fonction de un et en déduire la nature de la suite.
un+1 = 0,5 un, suite géométrique de raison q = 0,5 et de premier terme 60.
3. Exprimer un en fonction de n et déterminer l'activité après 5 demi-vies..
un = 60 x 0,5n ; u5 = 60 x0,55 = 1,875.
4. Déterminer le plus petit entier n à partir duquel un < 0,25.
60 x 0,5n <0,25 ;
0,5n < 0,25 / 60 ;
n < ln(0,25 / 60) / ln(0,5) ; n > 7,9 ( n > 8).
5. La demi-vie du
Thallium est d'environ 3 jours, déterminer le nombre de jours au bout
duquel on est certain que l'activité est strictement inférieure à 0,25
MBq.
3 x 7,9 =23,7 ~ 24 jours.
|
|