Mathématiques,
Bac St2S Antilles 09 / 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Exercice
1. (9 points)
La
Direction de la recherche, des études, de l’évaluation et des
statistiques (Drees) collecte des informations sur les établissements
d’accueil des enfants demoins de 6 ans.
Les parties A et B de cet exercice sont indépendantes.
Partie A :
Ces établissements d’accueil se caractérisent notamment par leurs modes
d’accueil : l’accueil en multiaccueil, en monoaccueil ou l’accueil
familial.
Une enquête de la Drees révèle qu’au 31 décembre 2013, en France métropolitaine :
• 31,1% des établissements sont des structures monoaccueil dont 58,8% sont gérées par des organismes publics.
• 63,6% des établissements sont des structures multiaccueil dont 55,6% sont gérées par des organismes publics.
• Les autres établissements sont des structures d’accueil familial dont 91% sont gérées par des organismes publics.
On choisit un établissement au hasard dans l’ensemble des établissements d’accueil. On considère les évènements suivants :
– A : « l’établissement est une structure monoaccueil » ;
– B : « l’établissement est une structure multiaccueil » ;
– C : « l’établissement est une structure d’accueil familial » ;
– D : « l’établissement est géré par un organisme public ».
1. À partir des données de l’énoncé, déterminer :
a. La probabilité de l’évènement A.
P(A) = 0,311.
b. La probabilité que l’établissement soit géré par un organisme public sachant qu’il s’agit d’une structure multiaccueil.
PB(D) =0,556.
2. Compléter l’arbre de probabilité qui représente la situation.
3. Dans cette question les probabilités calculées seront arrondies au millième.
a. Décrire par une phrase l’évènement A∩D et calculer la probabilité de cet évènement.
P(A n D) = 0,311 x0,588 ~0,183.
18,3 % des établissements sont des structures monoaccueil et sont gérés par des organismes publics.
b. Montrer que la probabilité que l’établissement soit géré par un organisme public est environ égale à 0,585.

4. Un journaliste
affirme que parmi les établissements gérés par des organismes non
publics, environ 2 sur 3 sont des structures multiaccueil.
Cette affirmation est-elle vraie? Justifier la réponse.

L'affirmation est vraie.
Partie B :
Le tableau suivant recense le nombre total d’établissements multiaccueil entre 2009 et 2013 en France métropolitaine.
Année
|
2009
|
2010
|
2011
|
2012
|
2013
|
Rang xi de l'année
|
0
|
1
|
2
|
3
|
4
|
Nombre yi d'établissements multiaccueil
|
5720
|
6250
|
6900
|
7560
|
8050
|
1. Calculer le taux d’évolution du nombre d’établissements multiaccueil entre 2009 et 2013. Arrondir à 0,1%.
(8050-5720) / 5720 ~0,41 %.
2. Représenter le nuage de points de coordonnées (xi ; yi ) associé aux données du tableau précédent.
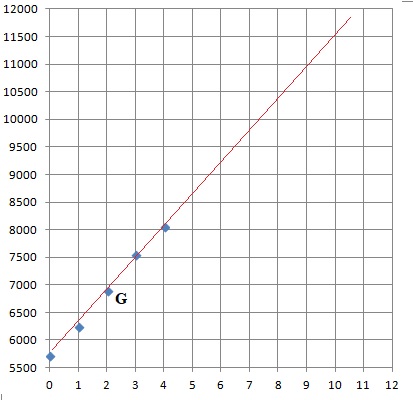
3. Calculer les coordonnées du point moyen G de ce nuage de points. Placer le point G sur le graphique.
xG=(0 +1 +2 +3 +4) / 5 =2.
yG = (5720 + 6250 +6900 +7560 +8050) / 5 = 6896.
4. On admet que la
droite D d’équation y = 597x +5702 réalise un bon ajustement affine du
nuage de points et que cet ajustement reste valable jusqu’en 2018.
a. Montrer que le point G appartient à cette droite D.
y = 597 x 2 +5702 = 6896 = yG.
b. Tracer la droite D sur le graphique .
c. Selon ce modèle, déterminer une prévision du nombre d’établissements multiaccueil
en 2018. Indiquer la méthode utilisée.
En 2018, x = 9. Le graphe indique 11 000.
Le calcul donne : 597 x 9 +5702 =11075.
|
|
|
|
|
Exercice 2. 6 points.
Dans une usine pharmaceutique, une unité de production fabrique un médicament qu’elle vend par lots. Sa capacité de production est limitée à 60 lots par mois.
Partie A :
Sur le graphique suivant, est représenté le bénéfice, en euros, en fonction du nombre de lots fabriqués et vendus en un mois.
1. Avec la précision permise par le graphique et en faisant apparaître les traits utiles à la lecture :
a. Déterminer le bénéfice, en euros, correspondant à la fabrication et à la vente en un mois de 10 lots de ce médicament.
b.
Déterminer le nombre de lots que l’usine pharmaceutique doit fabriquer
et vendre en un mois pour obtenir un bénéfice de 6 000 euros.
c.
Pour quels nombres de lots fabriqués et vendus en un mois, l’usine
pharmaceutique réalise-t-elle un bénéfice supérieur ou égal à 14 000
euros ?
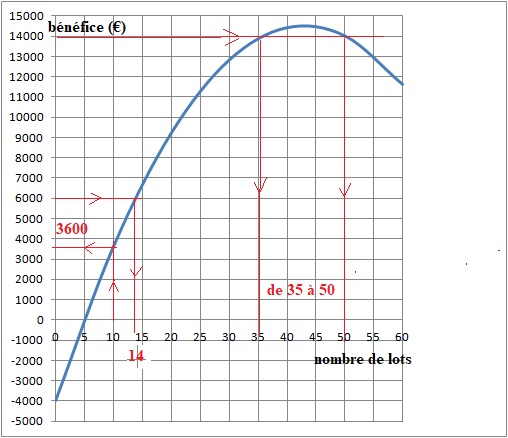
2. Pour quels nombres de lots fabriqués et vendus en un mois, la production est-elle rentable ?
Le bénéfice est positif à partir de 5 lots.
Partie B :
On
admet que le bénéfice en fonction du nombre de lots fabriqués et vendus
en un mois est modélisé par la fonction f définie sur l’intervalle [0;
60] par
f (x) = −10x2 +860x −4000.
1.
La fonction f ′ est la fonction dérivée de la fonction f . Déterminer f
′(x) pour tout réel x appartenant à l’intervalle [0; 60].
f '(x) = -20x +860.
2. Étudier le signe de f ′(x) sur l’intervalle [0; 60]. Dresser le tableau de variations de la fonction f sur l’intervalle [0; 60].
f '(x)= 0 pour x = 43 ; f '(x) >0 pour x appartenant à [0 ; 43] ; f '(x) est négative pour x appartenant à [43 ; 60].
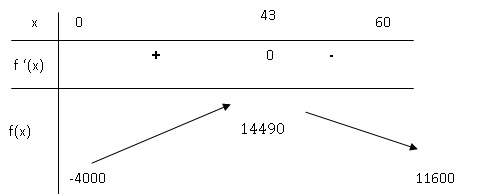
3. En déduire le bénéfice maximal ainsi que le nombre de lots fabriqués et vendus correspondant à ce bénéfice maximal.
f(43) = -10 x432 +860 x43 -4000=14 490.
|
|
Exercice 3. 5 points.
Lors
d’une culture in vitro de bactéries Escherichia coli on s’intéresse à
la phase de croissance exponentielle lors de laquelle, dans les
conditions optimales de température à 37°C, le nombre de bactéries
double toutes les 20 minutes.
Lors de la phase exponentielle, le temps nécessaire pour que le nombre
de bactéries double, ici 20 minutes, est appelé temps de génération.
On estime qu’au début de la phase exponentielle, le nombre de bactéries Eschericha coli par mL s’élève à 50 millions. Soit u0 le nombre de bactéries exprimé en millions au début de la phase exponentielle et un le nombre de bactéries après n temps de génération, c’est-à-dire après n fois 20 minutes.
On a ainsi u0 = 50.
1. a. Calculer u1 et u2.
u1 = 2 u0 = 100 ; u2 = 2 u1 = 200.
b. Montrer que u3 = 400 et interpréter la valeur de u3.
u3 = 2 u2 = 400. Au bout de 60 minutes ( une heure ) le nombre de bactéries est égal à 400 millions par mL.
2. a. Quelle est la nature de la suite (un) ?
b. Exprimer un en fonction de n.
La suite est géométrique de raison q = 2 et de premier terme u0 = 50.
un = 50 x2n.
c. Calculer le nombre de bactéries par mL au bout de 2 heures de phase exponentielle.
2 heures = 6 x 20 minutes ; n = 6.
u6 = 50 x26 = 3200.
3. a. Déterminer la plus petite valeur entière n telle que 50×2n >200000.
ln (50) + n ln(2) > ln(200 000) ;
n > [ln(200 000 )- ln(50) ] / ln(2) ; n > 11,96 ; n > 12.
b. Est-il vrai qu’après 4 heures de phase exponentielle le nombre de bactéries par mL sera supérieur à 200 milliards ?
4 heures = 20 x 12 minutes.
50 x 212 = 204 800 millions = 204,8 milliard. C'est vrai.
4. Une personne affirme qu’après 48 heures de phase exponentielle, le nombre de bactéries par mL sera supérieur à 1045.
Que pensez-vous de cette affirmation ?
Faux. Il y a épuisement du milieu de culture et accumulation des déchets.
|
|