Mathématiques,
Bac St2S Polynésie 09 / 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Exercice
1. (5 points)
Le
service social d’une ville souhaite mener une étude sur les modes de
garde choisis par les familles pour leurs enfants de moins de 3 ans.
Une famille est composée des enfants et de leurs parents, vivant en
couple ou pas.
Un questionnaire a été rempli par un échantillon de 1 000 familles ayant au moins un enfant de moins de 3 ans.
L’examen des réponses apportées par ces familles à ce questionnaire donne les informations suivantes ::
• 70% des parents vivent en couple et 60% de ces couples ont choisi de garder eux-mêmes leurs enfants durant la semaine.
• Parmi les parents ne vivant pas en couple, 30% d’entre eux ont choisi de garder eux-mêmes leurs enfants durant la semaine.
On choisit au hasard un questionnaire. Chaque questionnaire a la même probabilité d’être choisi.
On considère les évènements suivants :
C : « Le questionnaire est celui d’une famille dont les parents vivent en couple » ;
G : « Le questionnaire est celui d’une famille dont les parents gardent eux-mêmes leurs enfants durant la semaine ».
1. En utilisant les données fournies par l’énoncé :
a. calculer la probabilité que le questionnaire soit celui d’une famille dont les parents ne vivent pas en couple.
P(non C) = 1-0,7 = 0,3.
b. donner les probabilités PC (G) et Pnon C (G) et leur interprétation dans le contexte de l’exercice.
PC (G) =0,6 ; 60 % des parents vivant en couple garde leurs enfants.
Pnon C (G) = 0,3 ; 30 % des parents ne vivant pas en couple garde leurs enfants.
2. Reproduire sur la copie l’arbre pondéré de probabilités ci-dessous, puis le compléter :
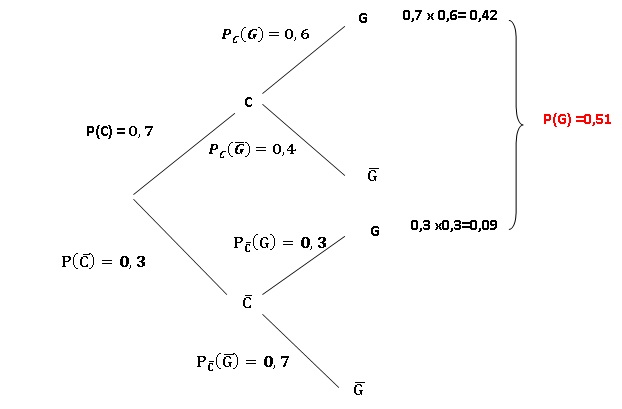
3. Calculer la probabilité de l’évènement C ∩G.
P(C n G) = 0,7 x0,6 = 0,42.
4. Montrer que P(G) = 0,51.
P(G) = P(C n G) + P(non C n G) = 0,42 + 0,3 x0,3 = 0,42 +0,09 = 0,51.
5. Le questionnaire
choisi est celui de parents gardant eux-mêmes leurs enfants durant la
semaine. Calculer la probabilité que ces parents vivent en couple.
Arrondir le résultat au centième.
PG C = P(G n C) / P(G) = 0,42 / 0,51 = 0,82.
|
|
|
|
|
Exercice 2. 6 points.
Marion
est salariée dans le même laboratoire pharmaceutique depuis quinze ans.
Elle souhaite étudier l’évolution de son salaire, qui dépend de ses
années d’ancienneté, de la politique salariale de l’entreprise, des
augmentations occasionnelles, etc.
Afin d’estimer son salaire en 2020,Marion a reporté dans la feuille de
tableur ci-dessous les montants de son salaire mensuel moyen entre 2010
et 2017.
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
1
|
Année
|
2010
|
2011
|
2012
|
2013
|
2014
|
2015
|
2016
|
2017
|
2
|
Rang de l'année xi |
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
3
|
Salaire mensuel moyen (€) yi
|
1650
|
1725
|
1740
|
1756
|
1825
|
1850
|
1950
|
1960
|
4
|
Taux d'évolution %
|
|
4,5
|
|
|
|
|
|
|
Les
cellules de la plage B3 : I3 sont au format « Nombre », arrondi à
l’unité, et celles de la plage C4 : I4 sont au format « Pourcentage »,
arrondi à 0,1%.
Partie A.
1. a. Calculer le taux d’évolution du salaire moyen entre 2011 et 2012. Donner le résultat en pourcentage, arrondi à 0,1%.
(1740-1725) / 1725 x 100 = 0,869 ~0,9 %.
b.
La ligne 4 du tableau indique les taux d’évolution du salaire mensuel
moyen, d’une année sur l’autre. Quelle formule, entrée dans la cellule
C4, puis recopiée vers la droite, permet d’obtenir les taux d’évolution
voulus dans les cellules de la plage C4 : I4 ?
=(C3-B3)/B3
2. Calculer le
taux d’évolution global du salaire mensuel moyen entre 2010 et 2017.
Donner le résultat en pourcentage, arrondi à 0,1%.
(1960-1650) /1650 x 100 = 18,79 ~18,9 %.
Partie B.
On envisage de modéliser par un ajustement affine l’évolution du salaire mensuel moyen.
On a représenté, dans un repère orthogonal, le nuage de points de coordonnées (xi ; yi ) associé à cette série statistique.
1. Calculer les coordonnées du point moyen G du nuage et placer G dans le repère précédent.
xG=(1 +2 +3 +4 +5 +6 +7 +8) / 8 = 4,5
yG =( 1650 +1725 +1740 +1753 +1825 +1850 +1950 +1960) / 8 =1807 €.
2.
On considère la droite D d’équation y = 44x +1609. On admet que cette
droite réalise un ajustement affine de cette série, valable jusqu’en
2030.
a. Tracer la droite D dans le repère. Indiquer les coordonnées des points utilisés.
Point de coordonnées (0 ; 1609) et le point G.
b.
Déterminer graphiquement, en laissant apparents les traits de
construction, en quelle année Marion pourrait atteindre un salaire
mensuel moyen de 2 200 €.
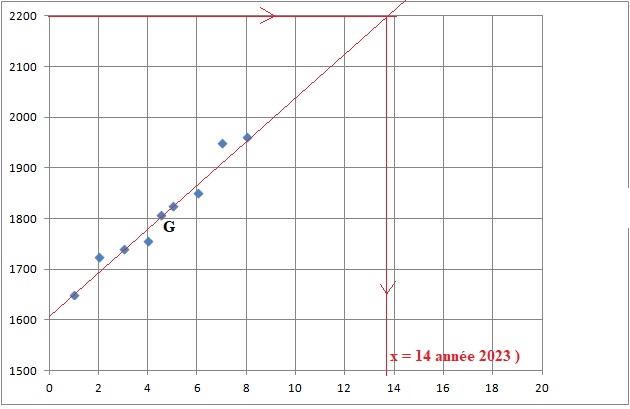
c. Selon ce modèle, calculer une estimation du salaire mensuel moyen de Marion en 2020.
x = 11 ; y = 44 x 11 +1609 =2093 €.
|
|
Exercice 3. 9 points.
L’empreinte
carbone est un indicateur des émissions de gaz à effet de serre qui
intègre les émissions directes des ménages français (logements et
voitures), les émissions de la production nationale (hors
exportations), et celles associées aux produits importés.
Le tableau ci-dessous indique les émissions de CO2 de la France selon l’empreinte carbone entre 1995 et 2015. Les émissions sont exprimées en million de tonnes équivalent CO2.
Année
|
1995
|
2000
|
2005
|
2010
|
2015
|
Rang de l'année xi
|
0
|
5
|
10
|
15
|
20
|
Emission CO2 yi
|
477
|
534
|
592
|
573
|
532
|
Source : SOeS d’après Citepa, Eurostat, Insee, Douanes, AIE, 2016
On a représenté, dans un repère orthogonal, le nuage de points de coordonnées (xi ; yi ) associé à cette série statistique.
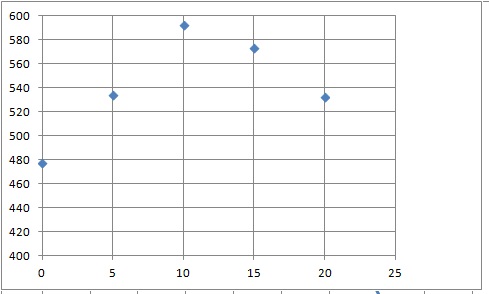
À l’issue de la conférence sur le climat en 2016, la France s’est engagée, d’ici 2030, à réduire ses émissions de CO2 de 40%, par rapport à leur niveau en 1990, estimé à 468 millions de tonnes équivalent CO2.
Le but de l’exercice est de prévoir la quantité de CO2 émise en 2030 à partir de deux modélisations différentes.
Les parties A et B sont indépendantes.
Partie A.
On propose de modéliser l’évolution des émissions de CO2 par la fonction f définie sur l’intervalle [0; 39] par :
f (x) = −0,8x2 +19,2x +470.
1. Déterminer la fonction dérivée f ′ de la fonction f sur l’intervalle [0; 39].
f '(x) = -1,6 x +19,2.
2. Étudier le signe de la fonction f ′ et en déduire le tableau de variation de la fonction f sur l’intervalle [0; 39].
f '(x) = 0 si 1,6 x = 19,2 soit x = 12.
f '(x) est positive sur [ 0; 12[ et négative sur ]12 ; 39].
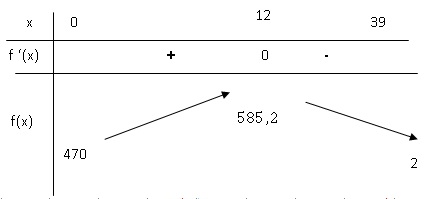
3. a. Compléter la deuxième ligne du tableau de valeurs. Les résultats seront arrondis à l’unité.
x
|
0
|
5
|
10
|
15
|
20
|
25
|
30
|
35
|
39
|
f(x)
|
470
|
546
|
582
|
578
|
534
|
450
|
326
|
163
|
2
|
b. En utilisant le tableau de valeurs précédent, tracer la courbe représentative de la fonction f sur l’intervalle [0; 39].
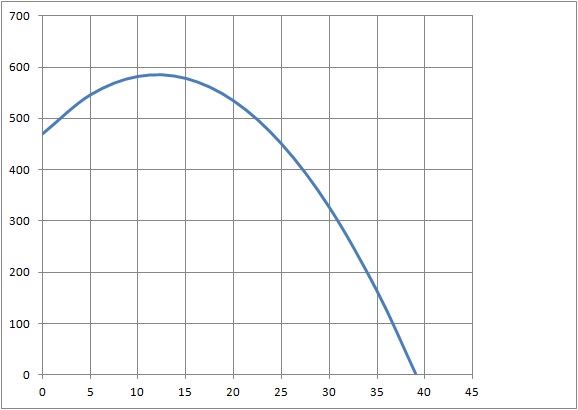
4. D’après ce premier modèle, l’engagement de la France sera-t-il tenu en 2030 ? Justifier la réponse.
Réduction des émissions de CO2 de 40%, par rapport à leur niveau en 1990, estimé à 468 millions de tonnes équivalent CO2.
468 *(1-0,4)=280,8.
f(39) = 2, valeur inférieure à 280,8. L'engagement est respecté, d'après ce modèle.
Partie B
On fait l’hypothèse qu’à partir de 2015, les émissions de C02 baissent annuellement de 3%. On modélise alors les émissions de CO2 à l’aide d’une suite numérique (un). Pour tout entier naturel n, un est égal aux émissions de CO2, en million de tonnes équivalent CO2, durant l’année (2015+n). Ainsi, u0 = 532.
1. a. Montrer que u1 = 516,04.
u1 = u0(1-0,03 ) =532 x 0,97 = 516,04.
b. Quelle est la nature de la suite (un) ? Préciser son premier terme et sa raison.
On passe d'un terme au suivant en le multipliant par 0,97. C'est une suite géométrique de raison 0,97 et de premier terme 532.
c. Pour tout entier n, exprimer un en fonction de n.
un = 532 x0,97n.
2. D’après ce second modèle, l’engagement de la France sera-t-il tenu en 2030? Justifier la réponse.
En 2030, n = 15 ; u15 = 532 x 0,9715 = 336,9.
Cette valeur est supérieure à 468 *(1-0,4)=280,8. L'engagement n' est pas respecté, d'après ce modèle.
|
|