Mathématiques,
Bac Sti2d, STL, biotechnologies, Antilles 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Exercice
1.
L’utilisation d’un antiseptique permet de diminuer la population de bactéries.
Le tableau ci-dessous donne le nombre de bactéries en fonction du temps en minutes.
Temps (min) ti
|
0
|
2
|
4
|
6
|
8
|
10
|
Nombre de bactéries ni
|
15000
|
11000
|
8400
|
6600
|
5500
|
4600
|
1. Représenter le nuage de points de coordonnées (ti ; ni ).
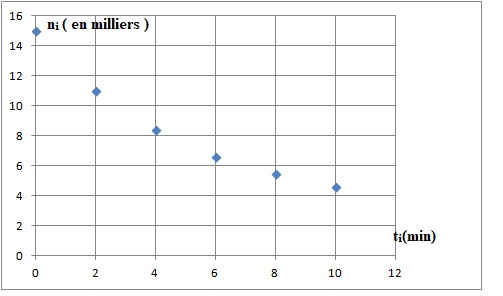
2. On estime qu’un ajustement affine n’est pas pertinent. On choisit d’effectuer un changement de variable en posant : yi = ln(ni )
a. Compléter le tableau suivant :
Temps (min) ti
|
0
|
2
|
4
|
6
|
8
|
10
|
yi=ln( ni)
|
9,616
|
9,306
|
9,036
|
8,795
|
8,613
|
8,434
|
b. Déterminer
une équation de la droite d’ajustement affine par la méthode des
moindres carrés de y en t . Les coefficients seront arrondis à 0,001.
y = -0,118 t +9,555.
3. Dans la suite,
on suppose que la droite d’ajustement affine de y en t obtenue par la
méthode des moindres carrés a pour équation y = −0,12t +9,55.
On admet que le modèle reste valable au-delà de 10 minutes.
a. Déterminer une estimation du nombre de bactéries au bout de 15 minutes. On arrondira le résultat à la centaine près.
y = -0,12 x15 +9,55 = 7,75 ; n = e7,75 ~2300.
b. Au bout de
combien de temps peut-on estimer que le nombre de bactéries sera
inférieur à 100 ? On donnera le résultat à la minute près.
ln 100 = 4,605 ; −0,12t +9,55 < 4,605 ;
0,12t >9,55-4,605 ; t > 41,2 ; t > 42 minutes.
Exercice 2.
En décembre 2017, Vincent emprunte 5 000 € à ses parents pour acheter une voiture.
Il décide de les rembourser le premier jour de chaque mois. Le 1er
janvier 2018, il effectue un premier versement de 100 €. Pour limiter
la durée du prêt, il décide ensuite d’augmenter les versements
de 2% chaque mois.
1. Quel montant verse-t-il le 1er février 2018?
100 x1,02 = 102 €.
2. On modélise la situation par une suite u On note un lemontant versé le n-ième mois. On a donc u1 = 100.
a. Justifier que la suite u est géométrique, préciser sa raison.
Le n+1 ième terme est obtenu en multipliant le n ième terme par 1,02.
Il s'agit d'une suite géométrique de raison 1,02 et de premier terme u1 = 100.
b. Exprimer un en fonction de n.
un = 100 x 1,02n-1.
c. Calculer, à 0,01 près, le montant que Vincent versera le 1er décembre 2018.
u12 = 100 x1,0211 = 124,34 €.
d. Vincent aura-t-il remboursé un quart de ce qu’il doit à ses parents le 30 décembre 2018 ?

500 / 4 = 1250 ; il a remboursé 1341,21 € le 1er décembre 2018, donc plus du quart de ce qu'il doit
3. On considère l’algorithme suivant :
n <-- 1
u <-- 100
S <--100
Tant que S < 5000
n <-- n+1
u <-- 1,02x u
S<-- S+u
Fin Tant que
a. Exécuter pas à
pas cet algorithme en remplissant le tableau avec les premières valeurs
successives prises par les variables u et S. On arrondira les résultats
au centime.
Valeur de n
|
1
|
2
|
3
|
4
|
Valeur de u
|
100
|
102
|
104,04
|
106,12
|
Valeur de S
|
100
|
202
|
306,04
|
412,16
|
b. Que représente le nombre inscrit dans la cellule grisée ?
La somme des 4 premiers remboursement.
c. Que représente la valeur de la variable n après l’exécution complète de l’algorithme ?
Il n’est pas attendu de la calculer.
Le nombre de mois pendant lesquels un remboursement a été effectué.
|
|
|
|
|
Exercice 3.
Une
catastrophe a rendu impropre à la consommation l’eau potable d’une
commune. L’eau du réseau contient une substance chimique dont
l’évolution de la concentration en fonction du
temps t écoulé depuis le début de la pollution est modélisée par la fonction f telle que :
f (t )= 30e−0,06t
La fonction f est définie sur [0 ; +∞[.
f (t ) est en mg·L−1 et t en heures.
1. Résoudre l’équation différentielle (E) : y′ +0,06y = 0.
y = A e-0,06t avec A une constante correspondant à la concentration initiale
2. Justifier que la fonction f est une solution de l’équation différentielle (E).
f '(x) = 30 x(-0,06) e−0,06t= -1,8e−0,06t.
Repport dans (E) : -1,8e−0,06t+0,06 x30e−0,06t = 0 est vrai quel que soit t..
3. Calculer f (0). Interpréter ce résultat.
La concentration initiale de la substance est f(0) = 30 mg L-1.
4. Quelle est la concentration, à 10−2 près, de la substance chimique dans l’eau au bout d’une journée ?
f(24) = 30e-0,06x24 = 7,11 mg L-1.
5. L’eau sera à nouveau consommable si la concentration de la substance chimique dans l’eau est inférieure à 0,05 mg·L−1. Au bout de combien de temps pourra-t-on de nouveau
consommer l’eau du robinet ?
0,05 = 30 e−0,06t ; e−0,06t =0,05 / 30 ;
-0,06 t = ln(0,05 / 30); t = ln(0,05 /30) / (-0,06) ~106,6 heures.
6. On
admet que la concentration moyenne de la substance chimique dans l’eau,
lors des douze premières heures, est donnée par la formule :
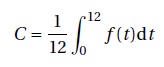
a. Vérifier que la fonction F définie sur [0 ; +∞[ par F(t )= −500e−0,06t est une primitive de f .
F '(t) = -500 x(-0,06)e−0,06t =30e−0,06t= f(t).
b. Calculer la valeur exacte de C.
C = [F(12) -F(0)] / 12 = -500 / 12 [e-0,06x12-1].
C = 125 / 3 (1-e-0,72).
c. Donner une valeur approchée à 10−2 près de la concentration moyenne de la substance chimique dans l’eau, lors des douze premières heures.
C ~ 21,39 mg L-1.
|
|
Exercice 4.
Une entreprise fabrique en grande série des éprouvettes de volume théorique 20 mL, destinées àêtre utilisées en laboratoire.
Les résultats seront donnés par des valeurs approchées, arrondies à 0,001.
PARTIE A :
On appelle X la variable aléatoire qui, à chaque éprouvette, associe son volume en mL.
X suit une loi normale dont la densité est représentée ci-dessous. On admet que l’écart-type de X est s = 0,01.
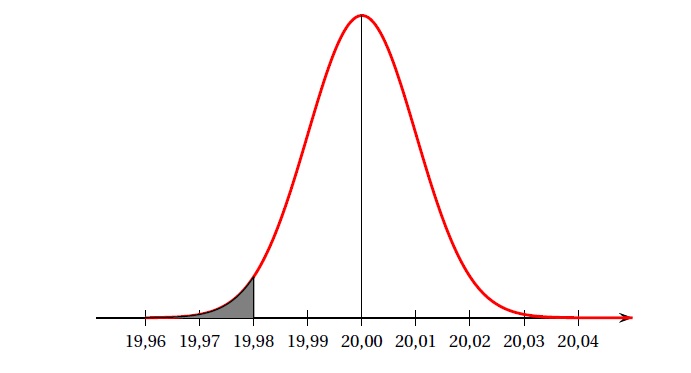
1. En utilisant le graphique, donner l’espérance de X.
µ=20,00.
2. Que représente l’aire de la partie grisée sur le graphique ?
P(X < 19,98).
3. Calculer la probabilité que le volume de l’éprouvette soit compris entre 19,975 mL et 20,025 mL
P(X < 19,975) =0,00621 ;
P(X < 20,025) =0,9938 ;
P(19,975 < X < 20,025) =0,9938 -0,00621 ~0,988.
PARTIE B :
Une éprouvette est dite conforme si son volume est compris entre 19,975mL et 20,025mL.
Un laboratoire commande un lot de 1 000 éprouvettes. Ces éprouvettes
sont prélevées dans le stock de manière aléatoire. On considère le
stock suffisamment grand pour que le prélèvement
soit assimilé à un tirage aléatoire avec remise. L’entreprise assure
que la probabilité qu’une éprouvette ne soit pas conforme, dans un tel
stock, est de 0,012.
1. Déterminer
l’intervalle de fluctuation asymptotique à 95%de la fréquence observée
d’éprouvettes non conformes dans un lot de 1 000 éprouvettes.
p = 0,012 ; n = 1000.
1,96 (p(1-p) / n)½ =1,96 (0,012 x0,988 / 1000)½ =0,00675
[ 0,012-0,00675 ; 0,012 +0,00675] soit [0,00525 ; 0,01875 ]
2. Dans ce lot de 1 000 éprouvettes, le laboratoire a trouvé 9 éprouvettes non conformes.
L’annonce faite par l’entreprise est-elle acceptable ?
9 /1000 = 0,009, cette valeur appartient à l'intervalle [0,00525 ; 0,01875 ]. L'annonce faite est acceptable.
|
|