Mathématiques,
Bac Sti2d, STL Métropole 09 / 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Exercice
1. (4 points)
Cet
exercice est un questionnaire à choix multiples. Pour chacune des
questions suivantes, une seule des quatre réponses proposées est exacte.
Aucune justification n’est demandée. Une bonne réponse rapporte un
point. Une mauvaise réponse, plusieurs réponses ou l’absence de réponse
à une question ne rapportent ni n’enlèvent de point.
1. Une forme exponentielle du nombre complexe z= −3+i3½ est :
a. −2 * 3½e−i p/6 ; b. 2 * 3½ei p/6 ; c. 2 * 3½ei 5p/6 (vrai); d. 12½e-i 5p/6 .
Module de z : |z| =[(-3)2 +(3½)2 ]½ = 12½ = 2 x 3½.
z / |z|= -3½/2 +0,5i = cos (5p/6) + i sin (5p/6) ; z = 2 * 3½ei 5p/6.
2. On considère le nombre complexe z =0,5 e-ip/4. Le nombre z2 est :
a. un nombre réel
b. un nombre complexe de partie réelle nulle. Vrai.
c. un nombre complexe de module 1
d. un nombre complexe de partie imaginaire positive
z2 = 0,52e-ip/2= 0,25 ( cos (-p/2) + i sin(-p/2) = -0,25 i.
3. Une variable
aléatoire T suit la loi uniforme sur un intervalle de la forme [2 ; x],
où x est un réel strictement supérieur à 2. Sachant que P(2 < T < 3) =
0,25, la valeur de x est :
a. 2,25 ; b. 6 vrai ; c. 8; d. 10.
P(2 < T < 3) =(3-2) / (x-2) = 0,25 ; 1 = 0,25(x-2) ; 4 = x-2 ; x = 6.
4.
Sur le graphique ci-dessous, la surface grisée est délimitée par la
courbe d’équation y =1 / x, l’axe des abscisses et les droites
d’équation x = e et x = a, où a est un réel strictement supérieur à e.
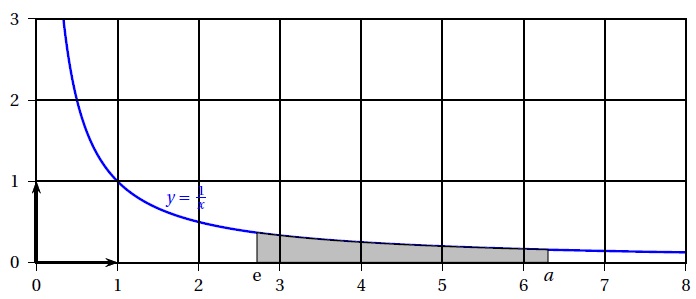
La surface grisée a une aire strictement comprise entre 1 et 1,5 unité d’aire lorsque a est égal à :
a. 2e ; b. 2e2 ; c. 3e vrai ; d. e2.
Aire hachurée A= [ln(x) ] ea =ln(a) - ln(e) = ln(a) -e.
Si a = 2e ; A = ln(2) +e -e ~0,69 ; si a = 2e2, A =ln(2) + 2e-e = ln(2) + e ~ 3,41.
Si a = 3e, A = ln(3) +e -e ~1,09 ; si a = e2, A = 2e-e = e ~2,7.
|
|
|
|
|
Exercice 2. 6 points.
Le
benzène est un produit chimique liquide utilisé dans la fabrication de
matières plastiques. À la suite d’un incident le 10 juin 2018, une
certaine quantité de benzène a été rejetée dans une rivière qui
alimente en partie un bassin servant de base nautique. Les autorités
sanitaires doivent s’occuper de la dépollution de la rivière tandis que
le responde la base nautique s’occupe de celle du bassin.sable
Le
benzène flotte à la surface de l’eau. Le responsable de la base
nautique prélève un échantillon de liquide selon un protocole établi.
Il détermine ainsi la concentration de benzène à la surface du bassin.
Celle observée le 10 juin 2018 est de 68 microgrammes par litre. Le
tableau suivant classe la qualité de l’eau selon la concentration de
benzène, exprimée en microgrammes par litre (μg/L), dans un échantillon
prélevé à la surface de l’eau.
Concentration en benzène ( µg / L)
|
[0 ; 0,5[
|
[0,5 ; 5 [
|
[ 5 ; 50 [
|
[50 ; 5000[
|
> 5000
|
Qualité de l'eau
|
excellente
|
bonne
|
moyenne
|
médiocre
|
mauvaise
|
La
toxicité du benzène par inhalation conduit le responsable à fermer la
base nautique afin de préserver la santé des usagers, cette décision
entraînant une perte de recette de 750 euros par jour.
La base nautique pourra rouvrir lorsque la qualité de l’eau sera
devenue excellente. Le responsable décide d’étudier deux solutions pour
dépolluer le bassin : la première consiste à laisser le benzène
s’éliminer sans intervention extérieure et la seconde consiste à
filtrer l’eau au charbon actif.
Partie A. Élimination du benzène de façon naturelle
Dans cette partie, le responsable étudie l’évolution de la
concentration de benzène à la surface du bassin sans intervention
extérieure. Il estime que cette concentration diminue de manière
naturelle de 7% par jour, notamment par évaporation.
1. a. Quelle est la qualité de l’eau le 10 juin 2018 ?
68 µg / L.
b. Quelle serait la qualité de l’eau le 11 juin 2018 ?
68 x(1-0,07) = 68 x 0,93 = 63,24 µg / L, eau médiocre.
2. Pour tout entier naturel n, on note un la concentration de benzène, en micro grammes par litre, à la surface du bassin n jours après le 10 juin 2018.
a. Montrer que la suite (un) est une suite géométrique dont on précisera le premier terme et la raison.
On passe d'un terme au suivant en le multipliant par 0,93. Il s'agit
d'une suite géométrique de raison q = 0,93 et de premier terme u0 = 68.
b. Déterminer une expression de un en fonction de n.
un = 68 x 0,93n.
c. Vérifier que le 15 juin 2018, l’eau deviendrait de qualité moyenne.
Le 15 juin, n = 5 ; u5 = 68 x0,935 = 47,3 µg / L.
Cette valeur est comprise entre 5 et 50:la qualité de l'eau est moyenne.
d. Quelle est la limite de la suite (un) ? Interpréter le résultat dans le contexte de l’exercice.
1 < 0,93 <1, donc 0,93n tend vers zéro quand n tend vers l'infini.
Au bout d'un temps suffisament long, tout le benzène s'est évaporé.
3. a. On propose ci-dessous la partie traitement de deux algorithmes.
Algorithme 1.
u <-- 68
n =0
Tant que u > 0,5
u <--0,93 u
n = n+1
Fin tant que
|
Algorithme 2.
u <-- 68
n =0
Tant que u < 0,5
u <--- 0,93 u
n = n+1
Fin tant que
|
Quel
est celui qui permettrait de déterminer le nombre de jours de fermeture
avant que la qualité de l’eau soit devenue excellente ?
La base nautique pourra rouvrir lorsque la qualité de l’eau sera devenue excellente, c'est à dire quand u < 0,5. Algorithme 1.
b. Déterminer le plus petit entier naturel n vérifiant l’inéquation 68×0,93n < 0,5. Indiquer la démarche utilisée.
ln(68) + n ln(0,93) < ln(0,5) ;
n < [ ln(0,5) - ln(68) ] / ln (0,93) ; n > [ ln(68) - ln(0,5) ] / (-ln (0,93)) ; n >67,7 ; n > 68.
c. Interpréter le résultat précédent.
La base nautique pourra rouvrir 68 jours après le 10 juin 2018.
d. En déduire la perte financière qui résulterait de la fermeture de la base si cette solution était retenue.
68 x750 = 51 000 €.
Partie B. Élimination du benzène par traitement au charbon actif
Un procédé de filtration de l’eau de la base nautique au charbon actif
permettrait d’éliminer plus rapidement le benzène présent à la surface
du bassin. Le coût total de l’installation est de 20 000 euros.
Dans cette partie, le responsable étudie cette solution. L’action du
filtre commencerait alors le 13 juin 2018. À la mise en service, à
l’instant t = 0, le responsable estime que la concentration de benzène
à la surface du bassin serait de 54,7 micrograrnrnes par litre.
Il choisit de modéliser la concentration de benzène en micro grammes
par litre à la surface du bassin, en fonction du temps t exprimé en
jours, par une fonction f , définie sur [0 ; +∞[ et vérifiant
l’équation différentielle :
(E) y′ +0,25y = 0.
1. Résoudre dans l’intervalle [0 ; +∞[ l’équation différentielle (E).
y = A e-0,25 t avec A une constante.
2. Justifier que, pour tout t >0, f (t )= 54,7e−0,25t .
A t = 0 : A e0 = A = 54,7.
3. Quelle serait la qualité de l’eau 19 jours après la mise en service du filtre ?
54,7 exp(-0,25 x19) = 54,7 exp(-4,75) = 0,473.
Partie C. Comparaison des deux solutions étudiées
Laquelle des deux solutions envisagées est financièrement la plus judicieuse pour la base nautique ?
19 x 750 + 20 000 = 34 250 €.
Le filtrage de l'eau au charbon actif est le plus judicieux.
|
|
Exercice 3.
6 points.
Une
société d’extraction de gravier reçoit une commande de 550 000 tonnes
de gravier pour la construction d’un tronçon d’autoroute. Pour
satisfaire cette commande, elle exploite un nouveau gisement de pierre.
Le responsable a recensé les masses journalières de gravier extraites
de ce gisement au cours de son exploitation. La tendance observée et
son expérience professionnelle le conduisent à modéliserla masse
journalière de gravier extraite, exprimée en tonnes, par la fonction f
définie sur
l’intervalle [0; 600] par : f (x) =( 0,2 x2 +30x)e-0,01x.
où x désigne le temps écoulé en jours depuis le début de l’exploitation du gisement.
Partie A.
1. a. Démontrer que, pour tout x de l’intervalle [0; 600],
f ′(x) = (−0,002x2 +0,1x +30)e−0,01x .
On pose u =0,2 x2 +30x et v = e-0,01x ; u' =0,4 x+30 ; v' = -0,01 e-0,01x ;
u'v + v'u = e-0,01x [(0,4x +30)-0,01(0,2 x2 +30x)]=(−0,002x2 +0,1x +30)e−0,01x .
b. Vérifier que, pour tout x de l’intervalle [0; 600],
f ′(x) = 0,002(−x +150)(x +100)e−0,01x.
0,002( -x2-100x+150x +15000)e−0,01x = (−0,002x2 +0,1x +30)e−0,01x = f '(x).
2. a. Étudier le signe de f ′(x) sur l’intervalle [0; 600].
f '(x) s'annule pour x = 150.
(x +100)e−0,01x est positif sur [0; 600].
f '(x) est positive si x appartient à [0 ; 150 [.
f '(x) est négaitive si x appartient à ]150 ; 600 ].
b. Dresser le tableau de variations de f sur l’intervalle [0; 600].
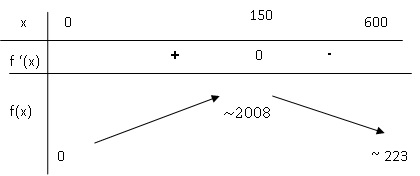
c. En déduire au bout de combien de jours la masse journalière de gravier extraite sera maximale.
Quelle est alors cette masse maximale, en tonnes ?
Au bout de 150 jours la masse de gravier est maximale et vaut environ 2008 tonnes.
3. La courbe représentative de la fonction f dans un repère orthogonal est donnée ci-dessous :
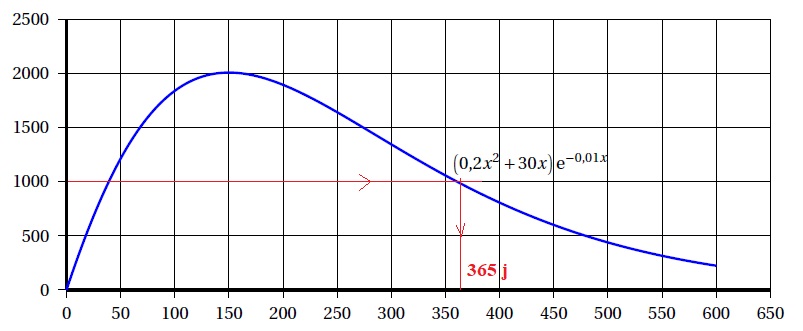
Après avoir atteint son maximum, la masse journalière de gravier extraite diminue.
Déterminer graphiquement au bout de combien de jours elle deviendra alors inférieure à 1 000 tonnes.
Répondre avec la précision permise par le graphique.
Partie B.
Un logiciel de calcul formel a permis d’obtenir les résultats suivants :
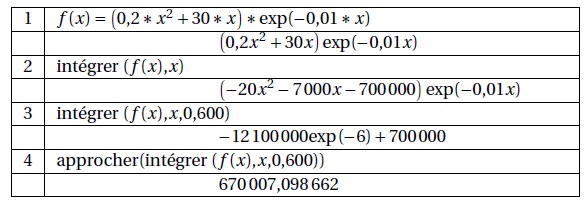
1. a. Que représente le résultat fourni par le logiciel en ligne 2 ?
Une primitive de f(x).
b. La commande pourra-t-elle être satisfaite au bout de 600 jours ?
Masse totale de gravier extraite : 670 000 tonnes, valeur supérieure à 550 000 t. la commande sera satisfaite.
2. Le responsable du chantier d’extraction estime que la commande sera satisfaite au bout de 400 jours.
Qu’en pensez-vous ? Justifier la réponse par un calcul.
Integrer f(x) entre 0 et 400 :
(-20 x4002 -7000 x400 -700000) exp(-0,01 x400) +700 000= -(3 200 000 +2 800 000 +700 000 ) exp(-4) +700 000= -122 714 +700 000 =577 285 t.
La commande sera satisfaite au bout de 400 jours.
Exercice 4 : 4 points.
Les parties A et B sont indépendantes.
Dans cet exercice, saufmention contraire, on donnera les résultats arrondis à 10−3 près.
Partie A.
1. Lors de la conception d’un avion, les techniciens cherchent à optimiser l’espacement entre les rangées de sièges.
L’espace minimal de confort, exprimé en centimètres, pour les jambes
d’un passager adulte peut être modélisé par une variable aléatoire L
qui suit la loi normale d’espérance μ = 55 et d’écart type s = 5.
Un passager adulte est choisi au hasard.
a. Calculer la probabilité que l’espace minimal de confort de ce passager soit compris entre 48 cm et 62 cm.
P(L < 48) = 0,15865 ; P(L < 62) = 0,8413 ;
P (48 < L < 62) = 0,8413 - 0,15865 ~0,683.
b. Calculer la probabilité que l’espace minimal de confort de ce passager soit supérieur à 67 cm.
P(L > 67) = 1 -P(L < 67) = 1-0,9567 ~ 0,043.
2. Sur cet avion
comportant 334 sièges, les techniciens fixent l’espace entre deux
rangées consécutives à 65 cm. La probabilité qu’un client adulte prenne
place confortablement est alors égale à 0,977.
On choisit au hasard un échantillon de 334 personnes adultes pour
prendre place dans cet avion. Le nombre de passagers confortablement
installés peut être modélisé par une variable aléatoire X.
a. On admet que la variable aléatoire X suit une loi binomiale. Préciser les paramètres de cette loi.
n = 334 ; p = 0,977.
b. Justifier qu’en moyenne, dans un tel avion, 326 personnes pourraient s’asseoir confortablement.
np = 334 x0,977 ~326.
c. Calculer P(X >330). Interpréter le résultat.
P(X >330) =1- P (X < 330) =1-0,949 = 0,051.
La probabilité que plus de 330 passagers soit assis confortablement est égale à 0,051.
Partie B.
Par expérience, la compagnie estime que la probabilité qu’un passager
ayant réservé une place se présente à l’embarquement est égale à 0,9.
La compagnie a accepté un nombre n de réservations supérieur ou égal à
335 pour 334 sièges disponibles. On suppose par ailleurs que les
comportements des passagers sont indépendants les uns des autres.
On note Y la variable aléatoire égale au nombre de passagers se présentant effectivement.
Y suit la loi binomiale de paramètres n et p = 0,9. Dans le tableau
ci-dessous, on donne, pour quelques valeurs de n supérieures à 335, la
probabilité pn qu’il y ait plus de personnes à l’embarquement que de places disponibles.
|
A
|
B
|
1
|
nombres n de places vendues
|
pn
|
2
|
353
|
0,0006
|
3
|
354
|
0,0012
|
4
|
355
|
0,0023
|
5
|
356
|
0,0041
|
6
|
357
|
0,0070
|
7
|
358
|
0,0115
|
8
|
359
|
0,0183
|
9
|
360
|
0,0280
|
10
|
361
|
0,0414
|
11
|
362
|
0,0594
|
1. Indiquer à 10−4 près la valeur manquante de la cellule B5 de ce tableau.
Loi binomiale : nombre de tirages : 356 : nombre de succès : 334 ; paramètre p = 0,9 ; cumulative.
p356=1-loi.binomiale (334; 356 ; 0,9 ; 1).
2. Combien de
billets au maximum la compagnie peut-elle vendre si elle souhaite que
le risque d’avoir plus de passagers que de sièges le jour de
l’embarquement soit inférieur à 2,5% ?
359, d'après le tableau.
|
|