Mathématiques,
Bac Sti2d STL, SPCL Polynésie 09 / 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Exercice
1. (4 points)
Cet
exercice est un questionnaire à choix multiples. Pour chaque question,
une seule réponse proposée est exacte. Une bonne réponse rapporte 1
point. Une réponse fausse, plusieurs réponses ou l’absence de réponse
ne rapportent ni n’enlèvent de point.
Indiquer sur la copie le numéro de la question et la lettre correspondant à la réponse choisie.
Aucune justification n’est demandée.
Le plan complexe est muni d’un repère orthonormé direct.
On désigne par i le nombre complexe de module 1 et d’argument p / 2.
1. Le nombre complexe solution de l’équation 3iz +1 = i est :
a. z = −1−2i ; b. z =1 / 3+ i / 3 (vrai); c. z = − 1 /3 ; d. z = −1/ 3−i / 3
On pose z = a + ib ; 3i(a+ib) +1 = i ; 3ia-3b +1 = i.
On identifie partie réelle et partie imaginaire : b = 1 /3 et a = 1 / 3.
2. On considère les deux nombres complexes z = 4 exp(ip /6) et z' = 2½exp(i3p /4)
Sur le graphique ci-dessous, le nombre z +z′ est représenté par le point :
a. A ; b. B ( vrai) ; c. C ; d. D.
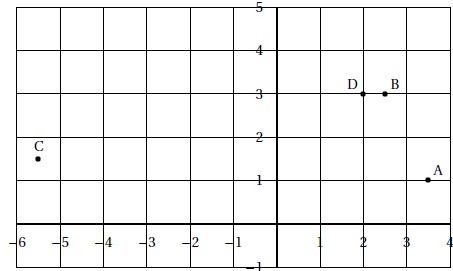
z = 4 ( cos (p / 6 )+ i sin (p / 6 )) = 2 x3½ + 2i.
z' = 2½ ( cos (3p /4 )+ i sin (3p / 4 ) )= -1+i.
z + z' = -1+2x3½ + 3i ~2,5 + 3 i.
3. On considère la fonction f définie sur I = ]-0,5 : +oo[ par f (x) =2 /(2x+1)
Une primitive de f sur I est la fonction F définie par :
a. F(x) = 2ln(2x +1) ; b. F(x) = −4 / (2x +1)2 ; c. F(x) =2x / (x2+x) ; d. F(x) = ln(2x +1). Vrai.
On pose u = 2x+1 ; u' = 2 ; f(u) = u' / u ; F(u) = ln(u) = ln(2x+1).
4. Le
graphique ci-dessous donne, dans un repère orthogonal, la
représentation graphique des fonctions f et g définies sur l’ensemble
des réels par :
f (x) = x2 −3x et g (x)= 3−x.
On souhaite connaître l’aire du domaine grisé. Cette aire, en unité d’aire, est égale à :
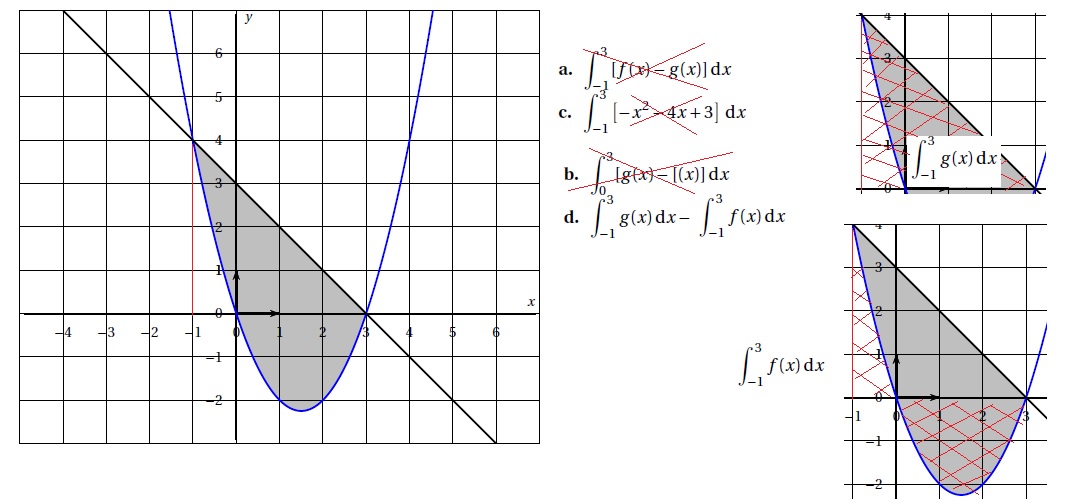
|
|
|
|
|
Exercice 2. 5 points.
Les parties A et B peuvent être traitées indépendamment l’une de l’autre. Les résultats seront arrondis au millième.
Un pâtissier utilise une machine pour fabriquer des gâteaux au chocolat
pesant en moyenne 500 grammes. Pour être commercialisable, un gâteau
doit peser entre 485 grammes et 515 grammes.
La masse, en gramme, d’un gâteau au chocolat peut être modélisée par
une variable aléatoire X qui suit la loi normale d’espérance μ = 500 et
d’écart type s = 11.
Partie A.
1. Calculer la probabilité que la masse d’un gâteau au chocolat soit supérieure à 515 grammes.
P(X >515) = 1 -P(X < 515) = 1-0,9137 ~0,086.
2. Calculer la probabilité p qu’un gâteau au chocolat choisi au hasard dans la fabrication soit commercialisable.
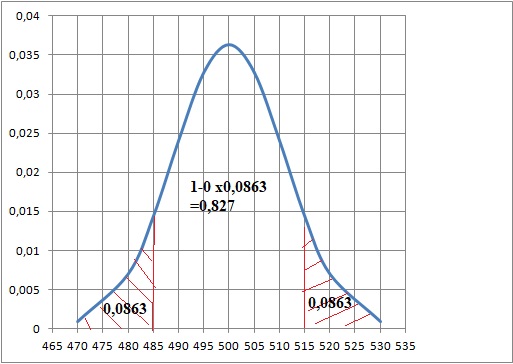
P(485 < X < 515 )= 0,827.
3. Le pâtissier trouve cette probabilité p trop faible.
Il décide de modifier ses méthodes de fabrication afin de faire varier
la valeur de l’écart type sans modifier celle de l’espérance μ.
On désigne par Y la nouvelle variable aléatoire modélisant la masse, en gramme, d’un gâteau au chocolat.
Cette variable aléatoire suit la loi normale d’espérance μ = 500 et d’écart-type s′.
Déterminer une valeur approchée de s′ pour que la probabilité qu’un gâteau au chocolat soit commercialisable ait pour valeur approchée 0,95.
On pose Z = (X -500) / s'.
P(485 < Z < 515) = 0,95 ; P (Z < 485) = (1-0,95) / 2 = 0,025.
s' = 6,7.
Partie B
Le
pâtissier utilise une balance électronique. La durée de fonctionnement
sans dérèglement, en jour, de cette balance électronique est une
variable aléatoire T qui suit la loi exponentielle de paramètre l.
1. On admet que la probabilité que la balance électronique ne se dérègle pas avant 30 jours est égale à 0,913.
Déterminer la valeur exacte de l puis la valeur arrondie au millième.
P (T > 30) = exp(-30 l) = 0,913 ; exp(-30 l) =0,913 ; -30 l = ln(0,913) ; l = -ln(0,913) / 30 ~0,003.
Dans la suite on prendra l= 0,003.
2.
Déterminer la probabilité que la balance électronique se dérègle durant
les 90 premiers jours. Arrondir le résultat au millième.
P(T > 90) = exp(-90 l) = exp(-90 x0,003) =0,7634.
Probabilité que la balance se dérègle durant les 90 premiers jours : 1-0,7634 ~ 0,237.
3.
Le vendeur de cette balance électronique a assuré au pâtissier qu’il y
a une chance sur deux que la balance ne se dérègle pas avant 365 jours.
A-t-il raison? Justifier la réponse.
P(T > 365) = exp(-365 l) = exp(-90 x0,003) =0,335
Probabilité que la balance se dérègle durant les 365 premiers jours : 1-0,335 ~ 0,665, valeur supérieure à 0,5.
Le vendeur a tord.
|
|
Exercice 3. 5 points.
La
consommation de soins et de biens médicaux (CSBM) en France comprend
les soins hospitaliers, les soins ambulatoires (médecins, dentistes,
auxiliaires médicaux, laboratoires d’analyse, thermalisme), les
transports sanitaires, les médicaments et les autres biens médicaux
(optique, prothèses,
petit matériel et pansements).
Partie A.
En 2008, la CSBM s’élevait à 164,7 milliards d’euros. Afin de mieux
maîtriser les dépenses de santé, le Gouvernement souhaitait que les
dépenses liées à la CSBM n’augmentent que de 2% par année.
On modélise l’évolution souhaitée par le Gouvernement par une suite (un) où un désigne le montant, en milliards d’euros, des dépenses pour l’année (2008+n). On a donc u0 = 164,7.
1. Déterminer la nature de la suite (un).
On passe d'un terme au suivant en le multipliant par 1,02. C'est une
suite géométrique de raison q = 1,02 et de premier terme 164,7.
2. Pour tout entier naturel n, exprimer un en fonction de n.
un = 164,7 x 1,02n.
3. Calculer u7. On donnera la valeur arrondie au dixième.
u7 = 164,7 x 1,027=189,2.
4. Interpréter cette valeur dans le contexte de l’exercice.
En 2015, la CSBM s'élèvera à 189,2 milliards d'euros.
Partie B.
Le tableau suivant, extrait d’une feuille d’un tableur, donne la CSBM réelle en milliards d’euros depuis l’année 2008 en France.
Dans cette partie, on ne demande pas de compléter le tableau.
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
1
|
Année
|
2008
|
2009
|
2010
|
2011
|
2012
|
2013
|
2014
|
2015
|
2
|
CSBM ( milliards € )
|
164,7
|
169,8
|
173,5
|
178,9
|
182,6
|
186,1
|
191,2
|
194
|
3
|
Evolution en %
|
|
|
|
|
|
|
|
|
1. a. Calculer le pourcentage d’évolution de la CSBM entre les années 2008 et 2015 arrondi à 0,01% .
(194 -164,7) / 164,7 x 100 = 17,79 %.
b. Les cellules C3
à I3 sont au format pourcentage. Proposer une formule à entrer en C3
qui, recopiée vers la droite jusqu’en I3, permet de déterminer le taux
d’évolution en pourcentage des dépenses entre deux années consécutives.
=(C2-B2)/B2
2. À partir de 2015, on suppose que la CSBM augmentera de 2,4% par année.
On veut déterminer, à l’aide de l’algorithme ci-dessous, l’année à partir de laquelle la CSBM dépassera 300 milliards d’euros.
a. Recopier et compléter l’algorithme.
N ←0
V ←194
Tant que V < 300
N ←N+1
V ←V x1,024.
Fin Tant que
b. Quelle est la valeur de la variable N après exécution de l’algorithme ?
c. En quelle année la CSBM dépassera-t-elle les 300 milliards d’euros ?
194 x1,024N > 300 ; 1,024N > 300 / 194 ; N ln(1,024) > ln(300 / 194) ; N > 18,38. On retient N = 19.
En 2015 +19 soit en 2034, la CSBM dépassera les 300 milliards d’euros.
Exercice 4. 6 points.
Partie A.
On considère la fonction w définie pour tout réel positif t par :
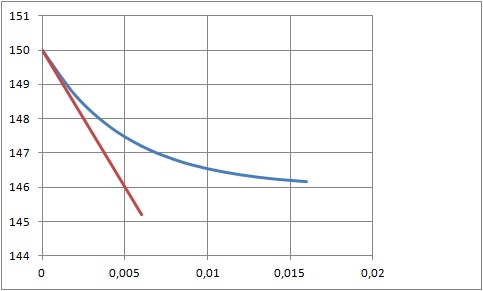
w(t ) = 4e-200t+146.
On note C la courbe représentative de la fonction w dans un repère orthonormé.
1. a. Calculer w(0).
w(0 ) = 4e0+146 = 4 +146 = 150.
b. Déterminer la limite de la fonction w lorsque t tend vers +∞ et interpréter graphiquement cette limite.
e-200ttend vers zéro quand t tend vers plus l'infini ; w(t) tend vers146.
La droite d'équation y = 146 est asymprote à la courbe C.
2. On note w′ la fonction dérivée de la fonction w sur l’intervalle [0 ; +∞[.
a. Pour tout réel positif t , calculer w′(t ).
w'(t) = 4 x(-200)e-200t = -800e-200t.
b. Étudier le signe de w′ sur l’intervalle [0 ; +∞[.
Le terme en exponentielle est positif ; w'(t) est négative sur l’intervalle [0 ; +∞[.
c. Dresser le tableau de variation de la fonction w sur l’intervalle [0 ; +∞[.
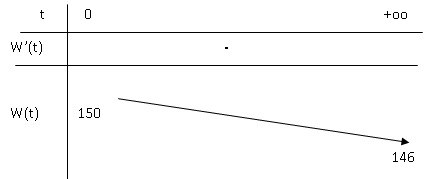
d. Déterminer une équation de la tangente à la courbe C au point d’abscisse 0 .
Coefficient directeur de la tangente : w'(0) = -800.
Equation de la tangente y = -800 t+ b.
la tangente passe par le point de coordonnées (0 ; 150) : 150 = b
y = -800 t +150.
Partie B.
On étudie l’évolution de la vitesse d’un moteur dont la vitesse de rotation à vide est de 150 rad·.s−1.
On s’intéresse à une phase particulière appelée phase d’embrayage.
Durant cette phase, la vitesse de rotation du moteur, exprimée en rad·.s−1, est modélisée par une fonction solution de l’équation différentielle (E) :
1 / 200 y′ + y = 146
où y désigne une fonction dérivable de la variable réelle t positive et exprimée en seconde.
1. a. Résoudre cette équation différentielle.
Solution générale de 'l"quation sans second membre : y = A exp(-200t)
Solution particulière de (E) : y = 146.
Solution générale de (E) : y = A e-200t +146 avec A une constante.
b. Vérifier que la
fonction w étudiée dans la partie A est la fonction solution de
l’équation différentielle (E) vérifiant la condition initiale w(0) =
150.
y (0) =150 = A +146 ; A = 4. y = 4 e-200t +146 = w(t).
2.
Interpréter, dans le contexte de l’exercice, la limite de w(t ) lorsque
t tend vers +∞ainsi que le sens de variation de la fonction w,
déterminés dans la partie A.
Quand t tend vers plus l'infini, la vitesse de rotation du moteur est constante.
Durand la phase d'embrayage, la vitesse du moteur diminue de 150 à 146 rad / s.
3. On considère que la vitesse de rotation dumoteur, exprimée en rad·.s−1, est stabilisée lorsque la quantité (w(t )−146) / 146 est inférieure à 0,01.
Calculer le temps mis par le moteur pour stabiliser sa vitesse. On
donnera la valeur exacte puis la valeur arrondie au millième de seconde.
(w(t )−146) / 146 = 4 / 146 e-200t < 0,01.
e-200t < 1,46 / 4 ; -200 t < ln(0,365) ; t > -ln(0,365) / 200 ; t > 0,005 s.
|
|