Physique,
concours ergothérapeute Berck 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
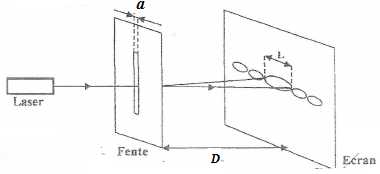
1. La lumière d'un laser de longueur d'onde l
est diffractée par une fente verticale de largeur a. On observe la
figure de diffraction sur un écran situé à la distance D de la fente.
On note L la largeur de la tache centrale de diffraction et q le demi-angle de diffraction.
l = 630 nm ; L = 20 mm; D = 2,0 m.
Calculer a (en mètre).
1,3 10-5 ; 1,3 10-4 ; 1,3 10-3 ; 6,3 10-4 ; 6,3 10-3 ; aucune réponse exacte.
tan q = ½L/D voisin de q radian pour les angles petits.
d'autre part
q =
l/a.
avec : l longueur d'onde (m) et a :
diamètre du fil (m)
en tenant
compte des deux relations ci-dessus : ½L/D=l/a soit a = 2l D/L
.a = 2 x 630 10-9 x 2,0 / (2,0 10-2)= 2 x 6,3 10-5 ~1,3 10-4 m.
2. Une source de lumière immobile émet un rayonnement lumineux de longueur d'onde l0.
Lorsque cette source s'éloigne à la vitesse v par rapport à un
observateur, ce dernier perçoit un rayonnement de longueur d'onde l, supérieure à l0.
On supposera que la vitesse de la source est très petite devant la célérité c de la lumière.
Parmi les propositions ci-dessous laquelle est exacte ?
l = l0 ( 1+v / c) : écriture homogène et l >l0. Vrai.
l = l0 ( 1-v2 / c2) : écriture homogène et l < l0.
l = l0 ( c-v) : l'écriture n'est pas homogène vis à vis des unités.
l = l0 ( c+v) : l'écriture n'est pas homogène vis à vis des unités.
l =( l0 ( c-v))½ : l'écriture n'est pas homogène vis à vis des unités.
3.
Un pendule simple est formé par un solide ponctuel de masse m, fixé à
un fil inextensible de longueur L de masse négligeable. Ce pendule
simple est suspendu par son extrémité libre en un point fixe. On écarte
le pendule de la verticale d'un angle q0
et on le lâche sans vitesse initiale à la date t=0. On prend pour
référence de l'énergie potentielle le point correspondant à la position
d'équilibre du solide. Les graphes ci-dessous donnent les variations
des énergies cinétique et potentielle en fonction du temps.
Masse du solide ponctuel m = 100 g ; période du pendule : T = 2 p(L / g)½ ; g = 10 m s-2.
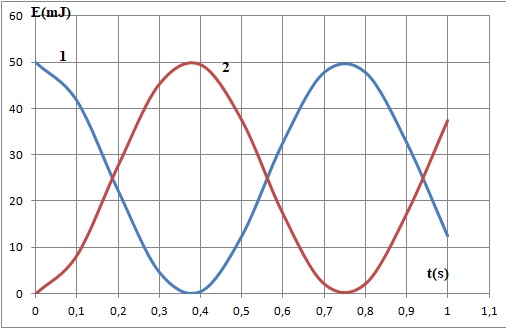
Combien y a-t-il d'affirmations exactes ?
La courbe 1 donne les variations de l'énergie potentielle de pesanteur en fonction du temps. Vrai. ( la vitesse initiale est nulle).
L'énergie mécanique est constante et vaut 25 mJ. Faux. ( énergie mécanique constante égale à 50 mJ ).
La vitesse du pendule s'annule à la date t = 0,75 s. Vrai. ( l'énergie cinétique est nulle).
Le pendule passe pour la première fois à sa position d'équilibre à la date t = 0,75 s. Faux. ( à la position d'équilibre, la vitesse, donc l'énergie cinétique, est maximale : t = 0,375 s ).
La vitesse maximale du pendule est 1 m /s. Vrai.
0,050 = 0,5 x0,100 v2 ; v2 =1 ; v = 1 m/s.
4. Calculer la longueur du fil ( en cm) constituant le pendule.
14 ; 28 ; 36 ; 56 ; 78 ; aucune réponse exacte.
La période de l'énergie cinétique ou de l'énergie potentielle est égale à la moitié de la période du pendule. T = 1,5 s.
L = T2 g / (4p2) ~1,52 x10 /(40) =2,25 / 4 ~0,56 m = 56 cm.
|
|
5.
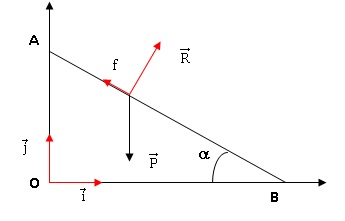
Un solide ponctuel S de masse m est abandonné sans vitesse initiale
d'un point A situé au sommet d'un plan incliné AB, incliné d'un angle a
par rapport à l'horizontale. S glisse suivant la ligne de plus grande
pente de ce plan. S est soumis à une force de frottement s'opposant au
mouvement et de valeur constante, notée f. La vitesse du solide en B
est notée vB.
xB = 2,0 m ; a = 30° ; vB = 4,0 m /s ; m = 0,50 kg. tan 30° = 0,58. cos 30 = 0,87.
Calculer en Joule la valeur du travail de la force de frottement entre A et B.
-1,8 ; -0,90 ; 0 ; 0,90 ; 1,8 ; aucune réponse exacte.
Variation d'énergie cinétique entre A et B : ½mvB2 = 0,5 x0,50 x4,02 = 4,0 J.
Travail moteur du poids entre A et B : m g OA = mg OB tan 30~ 0,5 x10 x2,0 x0,58 =5,8 J.
Travail résistant des frottements entre A et B : W = - f AB = - f OB / cos 30 = - 2 /0,87 f.
La variation d'énergie cinétique est égale à la somme des travaux des forces.
4,0 = 5,8 +W ; W = -1,8 J.
6. Combien y a t-il d'affirmations exactes ?
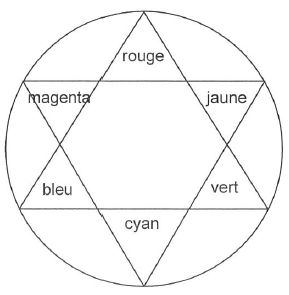
En synthèse additive, les trois couleurs primaires sont le cyan, le jaune et le magenta. Faux ( rouge, vert, bleu).
En synthèse additive, le bleu et le jaune sont des couleurs complémentaires. Vrai.
La superposition d'une lumière magenta et d'une lumière verte donne du noir. Faux. ( blanc).
Sous un éclairage cyan, un citron jaune paraît vert. Vrai.
Le citron jaune absorbe le bleu ; le cyan est un mélange de bleu et de vert.
Sous un éclairage jaune, une tomate rouge paraît noire. Faux.
Une tomate rouge absorbe le bleu et le vert. Le jaune contient le rouge et le vert.
.
|
|
7.
Une fibre optique de longueur L est utilisée pour transmettre un signal
numérique entre deux bâtiments. La puissance mesurée à l'entrée de la
fibre est PE = 5,0 mW et la puissance en sortie est PS = 1,0 mW. Le coefficient d'atténuation linéaire de cette fibre vaut a = 0,20 dB km-1.
Atténuation du signal A = 10 log (PE / PS). a = A / L. log 5 = 0,7.
Calculer la longueur L ( en km) de la fibre entre les deux bâtiments.
12 ; 17 ; 22 ; 31 ; 35 ; aucune réponse exacte.
A = 10 log (PE / PS) = 10 log ( 5 /1) = 10 x0,7 = 7 dB.
L = 7 / 0,20 = 35 km.
8.
La spectroscopie neutronique est une technique d'analyse de la
structure de la matière, basée sur la diffraction des neutrons. Un
faisceau homocinétique de neutrons est envoyé sur un échantikkon à
analyser. On considère que la vitesse des neutrons est v = 0,20 km /s.
Masse d'un neutron : 1,7 10-27 kg ; h = 6,6 10-34 J s. Angström = 10 -10 m.
Calculer la longueur d'onde en Angström du faisceau.
0,19 ; 1,9 ; 19 ; 5,1 ; 51 ; aucune réponse exacte.
l = h / (mv) =6,6 10-34 /(1,7 10-27 x200)=6,6 /(1,7 x2) 10-9=3,3 / 1,7 10-9 =1,9 10-9 m = 19 Angströms.
|
|