Fonctions
logarithme et exponentielle, Concours avenir.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
......
.....
|
2019.
21. Dans le plan muni d’un repère
orthonormé, on note D
la droite d’équation y = x.
Par ailleurs, pour n ∈N, on note (Cn) la courbe
représentative de la fonction définie par : f(x) =x2 +nx +1
Combien existe-t-il d’entier(s) naturel(s) n pour le(s)quel(s) (Cn)
et D n’ont aucun point en commun ?
a. 1 ; b. 2 ; c. 3 ; d. une
infinité. Vrai.
x2 +nx
+1 doit être différent de x soit x2 +(n-1)x +1 non nul.
x2
+(n-1)x +1=0 ; discriminant : (n-1)2-4 =0 ; n-1 =± 2 ; n =3
et n = -1 ( exclu).
n doit être différent de 3.
22. La limite, lorsque x tend vers 2
de (x2-x-2) / (x2-3x-2) est égale à :
a. 0 vrai ; b. +oo ; c. 2 ; d. 3.
Le dénominateur tend vers -4 et le numérateur tend vers zéro.
23. Le domaine de
définition de la fonction f, définie par :
f (x) = lnx / [(ln(x-3½) +ln(x+3½)].
x >0 et x-3½ > 0 soit x > 3½
et x+3½ > 0
soit x > -3½ .
x doit être
supérieur à 3½.
Le dénominateur ne doit pas être nul :
(ln(x-3½)
+ln(x+3½) = ln[x-3½)(x+3½)] =ln(x2-3)
différent de zéro soit x2-3 différent de 1 ; x différent de
±2
]3½ ; 2 [ union ]2 ; +oo[. Réponse
d.
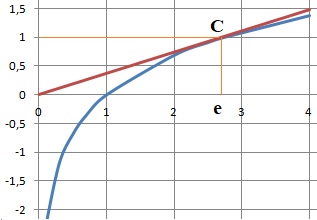
24. Dans le plan
muni d’un repère orthonormé, on note C la courbe représentative de la
fonction définie par f(x)= ln(x). L’ordonnée du point de C en lequel la
tangente à C passe par l’origine du repère est égale à :
a. 0 ; b. 1 vrai ; c. e ; d. −1.
Dérivée f '(x) = 1 /x. Coefficient directeur de la tangente à la courbe
au point C : 1 /xC.
Equation de la tangente à la courbe au point C passant par l'origine y = xC /
/xC =1.
25. Le domaine de
définition de la fonction f , définie par :
f (x) = ln(3x +2xex −xe2x ) est :
a. ]ln3 ; +∞[ ; b. ]−∞; 0[∪] ln3 ; +∞[ ; c. ]0 ; +∞[ ; d. ]0 ; ln3[ vrai.
3x +2xex
−xe2x > 0 ; x(3 +2ex-e2x) > 0 ;
Etude du signe
de 3 +2ex-e2x
en pose X = ex
positif ; 3 +2X-X2 =0.
Discriminant : 4 +12 = 16 ; solutions X1 =(-2 +4) / (-2) =
-1 (exclu) et X2 = +3 ;
x =ln(3) ; 3 +2X-X2
est positif sur ]0 ; 3[ ; 3
+2ex-e2x est positif sur ]0 ; ln(3) [.
26. Soit f la
fonction définie par f (x) = ln(ln(x½)). En notant f ′ la
fonction dérivée de f , on peut affirmer que l’expression de f ′(x) est
:
a. 1 /(x ln(x)) vrai ; b. 1 / ln(x½) ; c. 1/(x ln(x½)) ; d. 1
/(x ln(ln(x))).
On pose u = ln(x½) =0,5 ln(x) ; u' = 0,5 / x ; f '(x) = u' /
u = 0,5 / (x ln(x½)) = 0,5 /(0,5x ln(x)) = 1 /(x ln(x)).
27. Soit f la
fonction définie par f (x) = ln(x2 −9x −22). La limite de f
(x), lorsque x tend vers 11 par valeurs supérieures, est égale à :
a. 0+ ;
b. 0− ; c. −∞ vrai ; d. +∞.
Quand x tend vers
11+ : x2 −9x −22 tend vers 0+ ; ln(x2 −9x −22) tend vers moins
l'infini.
28. Dans
l’ensemble des nombres réels, l’équation e2x −1 = 6e−2x
admet :
a. aucune solution ;
b. une solution
strictement supérieure à ln(2½) ; vrai
c. une solution
strictement inférieure à ln(2½)
;
d. deux solutions
de signes contraires.
On pose X = e2x positif ; X-1 = 6 /X ; X2 -X-6=0
; discriminant : 25 ; solution retenue X =3 soit ln(3) = 2x ; x = 0,5 ln(3)~0,55.
Or ln(2½) ~0,35.
29. Soit f la
fonction définie sur R par f (x) = e2x +ex .
Dans le plan muni d’un repère orthonormé, on note (C ) la courbe
représentative de f et D
la droite d’équation y = x.
Combien (C ) possède-t-elle de tangente(s) parallèle(s) à D ?
a. 0 ; b. 1 vrai ; c. 2 ; d. 4.
Coefficient directeur des tangentes à la courbe C : f '(x) = 2e2x+ex.
Ces tangentes sont parallèles à la droite d'équation y = x.
2e2x+ex=
1 ; 2e2x+ex
-1 = 0.
On pose X = ex positif ; 2X2 +X-1 = 0 ;
discriminant : 9 ; solution retenue : X =0,5 ; x = ln(0,5).
30. Soit f la fonction définie sur R
par f (x) =(e2x-3) / (ex+1).
Dans le plan muni d’un repère orthonormé, combien la courbe
représentative de f possède-telle de tangente(s) parallèle(s) à l’axe
des abscisses ?
a. 0 vrai ; b. 1 ; c. 2 ; d. 3.
Calcul de f '(x) en posant u = e2x-3 et v = ex+1
; u' = 2e2x ; v' = ex ; f '(x) =[ 2e2x(ex+1) -ex(e2x-3)] / (ex+1)2.
f '(x) =(e3x+2e2x+3ex)
/ (ex+1)2
= ex(e2x+2ex +3) /
(ex+1)2 .
Coefficient directeur d'une tangente parallèle à l'axe des
abscisses : zéro.
e2x+2ex
+3 = 0 ; on pose X = ex ; X2 +2X+3=0 ;
discriminant négatif, aucune solution réelle.
31. Dans le plan
muni d’un repère orthonormé, on note (C ) la courbe représentative de f
, définie sur R, par f (x) = exp(x2+x+1).
Combien (C ) possède-t-elle de tangente(s) passant par l’origine ?
a. 0 ; b. 1 ; c. 2 vrai ; d. 4.
Calcul de la dérivée en posant X =x2+x+1 ; X' = 2x+1 ; f
'(x) = (2x+1)exp (x2+x+1).
Equation d'une tangente à la courbe passant par l'origine : y = f '(x) x .
Au point de tangence : exp(x2+x+1)
=(2x+1)exp (x2+x+1) x.
(2x+1)x =1 ; 2x2 +x-1 = 0 ; solutions -1 et +0,5.
|
...
|
|
2018.
Fonction exponentielle.
28) Pour tout nombre réel x, on a : 2-(ex+4) / (ex+2)
=
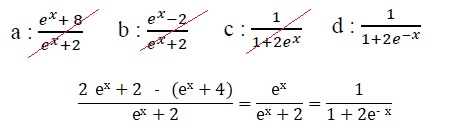
28)
Dans R , l’équation 1 / e2x =e4-x admet pour
solution
a : x = 4 /3.
b : x = -4 /3.
c : x = -4. Vrai.
d :x = 4.
e2x(e4-x)
= 1 ; e2x+4-x= 1 ; ex+4
= 1 ; x+4 = ln 1 = 0 ; x = -4 .
29.
On considère la fonction f définie sur ] -2 ; + oo[ par f(x) = -3e-x
/ (x+2). La fonction fest dérivable sur cet intervalle et f '(x) =
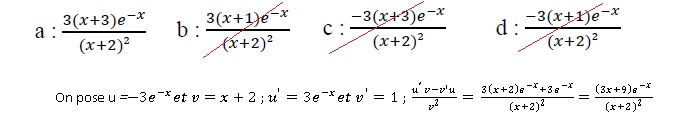
Pour
les questions 30 et 31, on considère les fonctions f et g définies sur
R par f(x) = 0,5(ex+e-x) et g(x) = 0,5(ex-e-x).
30 : Pour tout
nombre réel x , on a : ( f(x))2-(g(x))2 =
a : 1. Vrai.
b : ex.
c : -1
d : e-x.
( f(x))2-(g(x))2
=(f(x) + g(x)) . (f(x)-g(x)) = ex (e-x) = 1.
31 : Pour tous nombres réels x et y
, on a : f(x) *f(y) +g(x) *g(y) =
a :g(x+y).
b : g(x-y).
c : f(x+y). Vrai.
d : f(x-y).
f(x) *f(y)= 0,25(ex+e-x)(ey+e-y)=0,25 (ex+y+e-(x+y)+ex-y
+e-x+y) ;
g(x) *g(y) =0,25(ex-e-x)(ey-e-y)=0,25 (ex+y+e-(x+y)-ex-y
-e-x+y) ;
f(x) *f(y) +g(x) *g(y) =0,5 (ex+y+e-(x+y))=f(x+y).
Fonction logarithme népérien.
Pour les questions 34 à 40, on considère la fonction g(x) = ln(e2
/(f(x)) où f est une fonction dérivable sur dont le tableau de
variation est le suivant :
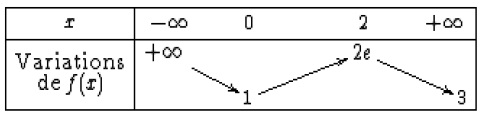
34 : g(0) =
a : 1
b : 2. Vrai.
c : e2.
d : Aucune des réponses précédentes n’est juste.
f(0) = 1 ; g(0) = ln(e2)
= 2 ln (e) = 2.
35 : En plus
l'infini, la limite de g(x) est :
a : -oo.
b : +oo.
c :0.
d : 2-ln(3). Vrai.
En plus l'infini, g(x)
est équivalent à ln(e2 / 3) = 2-ln(3).
36 : En moins
l'infini, la limite de g(x) est :
a : -oo. Vrai.
b : +oo.
c :ln(2) -ln(3).
d : Aucune des réponses précédentes n’est juste.
En moins l'infini, g(x)
est tend vers plus l'infini et e2 /(f(x)) tend vers
zéro ; ln(e2
/(f(x)) tend vers moins l'infini.
37 : La fonction
g(x) est dérivable sur R et g'(x) est donnée par :
a : -e2 f '(x) / f(x).
b : -f '(x) / f(x).
Vrai.
c : -e2 f '(x) / f(x)2.
d : -f '(x) / f(x)2.
On pose u = e2
/(f(x) ; u' = -e2 f '(x) / f(x)2.
Dérivée de ln (u) : u' / u soit -f '(x) / f(x).
38 : Dans le plan
muni d’un repère, la courbe représentative de la fonction g :
a : n’admet aucune asymptote.
b : admet
exactement une asymptote horizontale ou verticale. Vrai.
c : admet exactement deux asymptotes horizontales ou verticales.
d : Aucune des réponses précédentes n’est juste.
En plus l'infini, g(x)
est équivalent à ln(e2 / 3) = 2-ln(3).
39 :
L’équation g(x) = -100.
a : n’admet aucune solution dans R.
b : admet
exactement une solution dans R. Vrai.
c : admet exactement deux solutions dans R.
d : Aucune des réponses précédentes n’est juste.
40 :
L’équation g(x) = 3
a : n’admet aucune
solution dans R . Vrai.
b : admet exactement une solution dans R.
c : admet exactement deux solutions dans R.
d : Aucune des réponses précédentes n’est juste.
|
....
|
2016.
17.
Dans R l'équation admet e2x+ex+4 = ln((e-1) /17).
a. aucune solution.
Vrai.
b. exactement une
solution.
c. exactement deux
solutions.
d. exactement trois
solutions.
e2x+ex+4
est positif quel que soit x réel ; (e-1) /17 est inférieur à 1 ; ln((e-1) /17) est négatif.
18. Dans ]-p ; +p] l'équation sin(x) = ln
[exp(2x+3) / exp(2+2x) ] cos (x) admet :
a. aucune solution.
b. exactement une
solution.
c. exactement deux
solutions. Vrai.
d. exactement trois
solutions.
exp(2x+3)
/ exp(2+2x) = exp(2x+3-2x-2) = exp(1) = e ; ln(e) = 1.
sin(x) = cos(x) = sin ( p/2-x)
;
x = p/2-x +2kp et x =- p/2-x +2kp.
Fonction exponentielle.
19. On considère la fonction f
définie sur R par f(x)=(ex-2) / (ex+2), alors
pour tout x réel on a :
a. f '(x) = 2e2x
/(ex+2)2.
b.
f '(x) = (e2x -4)/(ex+2)2.
c.
f '(x) = 2ex /(ex+2)2.
d.
f '(x) = 4e2x /(ex+2)2. Vrai.
On pose u = ex-2 et v = ex+2 ; u' = v' = ex.
(u'v -v'u ) / v2=ex(ex+2 -ex+2) / (ex+2)2= 4ex
/ (ex+2)2.
20.
Quand x tend vers l'infini, la limite de x exp(1/x) est égale à :
a. 0 ; b. 1 ; c. -oo ; d. +oo. Vrai.
Quand x tend vers l'infini :
1/x tend vers zéro ; exp(1/x) tend vers 1 ; x exp(1/x) tend
vers + oo.
21.
Soient x et y deux nombres réels quelconques, on note A = exp((x+y)/2)
[exp((x-y)/2) +exp((y-x)/2)] et ,B = (exp(x) +exp(y) ) /e alors :
a. A=B ; b. A < B ; c. A >B Vrai ; c. On ne peut pas comparer A et B sans informations sur x et y.
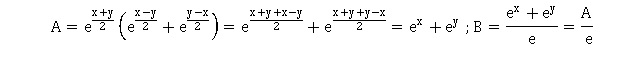 . .
22 . Quand x tend vers zéro, la limite de (e11x-e7x) / x est égale à : a. 0 ; b. +oo ; c. 4 Vrai ; d. 11 / 7.
e7x(e4x-1)/ x avec, au soisinage de zéro, e4x~1+4x.
(e4x-1) ~4x ; (e4x-1)/ x ~4 ; e7x ~1 ; e7x(e4x-1)/ x ~4.
Fonction logarithme népérien.
23. ln(16) +2 ln(3) -ln(24) est égal à :
a. 0 ; b. 2ln(3) ; c. ln(6) Vrai ; d. ln(5).
ln(16) +ln(9)-ln(24) = ln (16 x9 /24) = ln(6).
24. Pour tout x appartenant à ]-3 ; 3 [, ln(9-x2) est égal à :
a. 2ln(3)-ln(x).
b. ln(-3-x) +ln(-3+x).
c. ln(-3-x) ln(-3+x).
d. Aucune des 3 réponses précédentes n'est exacte. Vrai.
ln(9-x2)=ln[(3-x)(3+x)]= ln(3-x) +ln(x+3).
25. Quand x tend vers l'infini, la limite de 4x-3ln(x) est égale à :
a. 0 ; b. +oo Vrai ; c. -oo ; d. Aucune des 3 réponses précédentes n'est exacte.
Par croissance comparée, 4x croît plus vite que 3ln(x).
|
|