Nombres complexes, bac S 2018

Nombres complexes, bac S 2018.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
.

......

.....

Métropole.
On pose z₀ = 8 et pour tout entier naturel n : z_n+1 = (3 -i3^½) / 4 z_n.
On note A_n le point du plan d'affixe z_n.
1.a. Vérifier que : z= (3 -i3^½) / 4 = 3^½ / 2 exp(-ip/6).

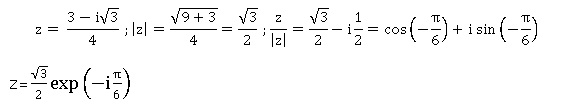
b. En déduire l'écriture des bombres complexes z₁, z₂ et z₃ sous forme exponentielle et vérifier que z₃ est un imaginaire pur dont on précisera la partie imaginaire.
z₁ =4 x 3^½ exp(-ip/6).
z₂ = 3^½ / 2 exp(-ip/6).z₁=6 exp(-ip/3)
z₃ = 3^½ / 2 exp(-ip/6).z₂=3 x 3^½ exp(-ip/2).
c. Représenter graphiquement les points A₀, A₁, A₂ et A₃.

2.a. Démontrer par récurrence que, pour tout entier naturel n , z_n = 8 (3^½/2)ⁿ exp(-inp/6).
Initialisation : la propriété est vraie au rang zéro.
Hérédité : la propriété est supposée vraie au rang n.

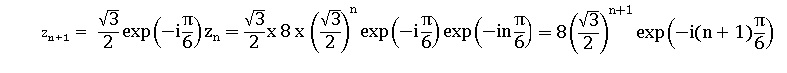
Conclusion : la prorpiété est vraie au rang zéro et héréditaire, elle est donc vraie pour tout entier naturel.
2.b. On pose u_n = |z_n|. Déterminer la nature et la limite de cette suite.
|z_n|= 8 (3^½ / 2)ⁿ = z₀ (3^½ / 2)ⁿ ; suite géométrique de premier terme 8 et de raison 3^½ / 2.
0 < 3^½ / 2 < 1, donc (3^½ / 2)ⁿ tend vers zéro quand n tend vers plus l'infini.
u_n tend vers zéro quand n tend vers plus l'infini.
3.a. Démontrer que pour tout entier naturel k : (z_k+1-z_k) / z_k+1= -i / 3^½.
En déduire que A_kA_k+1=OA_k+1 / 3^½.

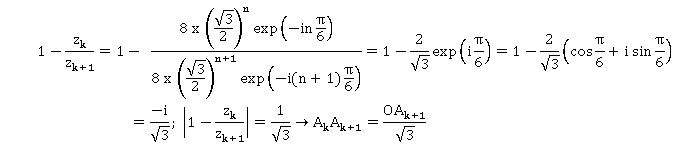
b. Pour tout entier naturel n , on appelle l_n la longueur de la ligne brisée reliant dans cet ordre les points A₀, A₁, A₂, ...A_n. Démontrer que la suite (l_n) est convergente et calculer sa limite.
.

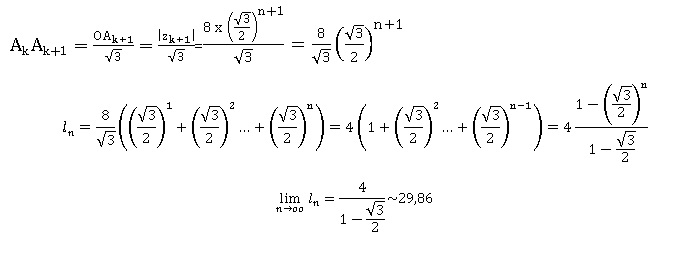Métropole septembre.
Le plan complexe est rapporté à un repère orthonormé direct. On prendra pour unité graphique le centimètre.
1. Résoudre dans C l’équation
(z²−2z +4)(z²+4)=0.
z2+4 = 0 ; z² = -4 = 4 i² ; z = ±2i.
z²−2z +4= 0 ; D = (-2)² -4 x4 = -12 = 12 i² = (±2 *3^½i)².
Solutions :(2 + 2 *3^½i) / 2 = 1 +3^½i et 1-3^½i.
2. On considère les points A et B d’affixes respectives z_A = 1+i3^½ et z_B = 2i.
a. Écrire z_A et z_B sous forme exponentielle et justifier que les points A et B sont sur un cercle de centre O dont on précisera le rayon.
|z_A| =(1+3)^½ = 2 ; z_A /|z_A| =0,5(1+i3^½ ) =cos (p/3)+ isin (p/3) ; z_A = 2 e^ip/3.
z_B = 2 e^ip/2.
OA = OB = 2.
Les points A et B sont sur un cercle de centre O et de rayon R = 2
b. Faire une figure et placer les points A et B.
c. Déterminer une mesure de l’angle (AOB).

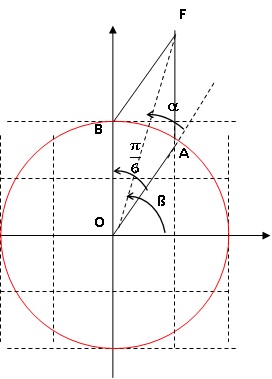
3. On note F le point d’affixe z_F = z_A +z_B.
a. Placer le point F sur la figure précédente.Montrer que OAFB est un losange.
z_F = z_A +z_B=1 + i(2+3^½).
AF = [0²+2² ]^½ =2 = OA = OB.
BF = [1²+(3^½)² ]^½ =2 = OA = OB.
Les quatre cotés du quadrilatère OAFB sont égaux.
De plus z_A-z_O = 1+i3^½ et z_F-z_B = 1+i3^½ ; z_A-z_O =z_F-z_B, le quadrilatère est un parallélogramme ayant deux cotés consécutifs égaux, c'est donc un losange..
b. En déduire une mesure des angles a et ß.
Les diagonales d'un losange sont perpendiculaires et axes de symétrie de la figure.
a = p /12 et ß = p /3 + p /12 =5 p /12.
c. Calculer le module de z_F et en déduire l’écriture de z_F sous forme trigonométrique.
z_F =1 + i(2+3^½) ; | z_F| =[ 1² + (2+3^½)²]^½=2(2+3^½)^½.
z_F =2(2+3^½)^½( cos(5 p /12) + i sin(5 p /12)).
d. En déduire la valeur exacte de cos(5 p /12).
2(2+3^½)^½( cos(5 p /12) + i sin(5 p /12)) = 1 + i(2+3^½).
On identifie les parties réelles :

.
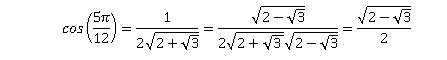
4. Deux modèles de calculatrice de marques différentes donnent :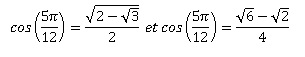
Ces résultats sont-ils contradictoires ? Justifier la réponse.
Ces résultats ne sont pas contradictoires.

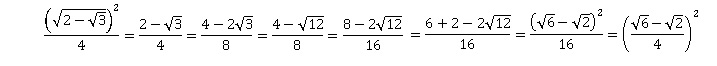
Liban.
1. Donner les formes exponentielle et trigonométriques des nombres complexes 1+i et 1-i.
Module de ces nombres complexes(1+1)½ = 2^½.
(1+i) / |1+i| = 1 / 2^½ + i /2^½ = cos (p/4) + i sin (p/4).
1+i = 2^½( cos (p/4) + i sin (p/4)) = 2^½exp(ip/4).

(1-i) / |1-i| = 1 / 2^½ - i /2^½ = cos (-p/4) + i sin (-p/4).
1-i = 2^½( cos (-p/4) + i sin (-p/4)) = 2^½exp(-ip/4).
2. Pour tout entier naturel n, on pose S_n = (1+i)ⁿ +(1-i)ⁿ.
a. Déterminer la forme trigonométrique de S_n.
S_n = 2^0,5n [ exp(i n p/4)+exp(-i n p/4)]
Or exp(i n p/4)+exp(-i n p/4) = 2 cos(n p/4).
S_n = 2 x 2^0,5n cos(n p/4).
b. Pour chacune des deux affirmations suivantes, dire si elle est vraie ou fausse en justifiant.
- Pour tout entier naturel n, le nombre complexes Sn est un réel. Vrai.

n
0
1
2
3
4
5
6
7
8

n p / 4
0
p/4
p/2 3p/4 p 5p/4 3p/2 7p/4 2p

cos(n p / 4)
1
2^-½
0
-2^-½ -1
-2^-½ 0
2^-½ 1

Si n =4 k +2 avec k entier naturel, S_n =0.
Si n = 8 k ou n= 1 +8k ou n=7+8k, S_n= 2 x 2^0,5n cos(n p/4) ( cos 0 + i sin 0) est un réel strictement positif.
Si n = 3+8 k ou n= 4 +8k ou n=5+8k, S_n= 2 x 2^0,5n cos(n p/4) ( cos p + i sin p) est un réel strictement négatif.

- Il existe une infinité d'entiers naturels tels qu S_n = 0. Vrai.
Si n =4 k +2 avec k entier naturel, S_n =0.

....

Asie.
Dans cet exercice, x et y sont des nombres réels supérieurs à 1.
Dans le plan complexe muni d’un repère orthonormé direct, on considère les points A, B et C d’affixes respectives
z_A = 1+i, z_B = x +i et z_C = y +i.

1. Démontrer que si OC =OA×OB, alors y² = 2x² +1.
OC = (y² +1²)^½ ; OA = (1² +1²)^½ =2^½ ; OB = (x² +1²)^½ ;
OA x OB = 2^½ (x² +1²)^½ = (2x² +1)^½ ;
(y² +1²)^½ = (2x² +2)^½ soit y² +1 =2x² +1 ; y² = 2x² +1.
2. Reproduire sur la copie et compléter l’algorithme ci-après pour qu’il affiche tous les couples (x, y) tels que :
y² = 2x² +1.
x et y sont des nombres entiers
1< x <10 et 1< y <10
Pour x allant de 1 à 10 faire
Pour y allant de 1 à 10 faire
Si y² = 2x² +1
Afficher x et y
Fin Si
Fin Pour
Fin Pour
Lorsque l’on exécute cet algorithme, il affiche la valeur 2 pour la variable x et la valeur 3 pour la variable y.
3. Étude d’un cas particulier : dans cette question seulement, on prend x = 2 et y = 3.
a. Donner le module et un argument de z_A.
|z_A|=(1²+1²)^½ = 2^½.
z_A / |z_A|=1 / 2^½ + i / 2^½ = cos (p/4) + i sin (p/4).
b. Montrer que OC =OA×OB.
y² =9 ; 2x² +1 =8+1 = 9 ; donc y² = 2x² +1 ; par suite OC =OA×OB.
c. Montrer que z_Bz_C = 5z_A et en déduire la relation suivante.
z_Bz_C =(2+i)(3+i) = 6+i²+5i =5(1+i) = 5 z_A.

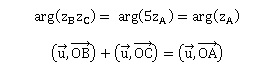
4. On revient au cas général, et on cherche s’il existe d’autres valeurs des réels x et y telles que les points A, B et C vérifient les deux conditions données ci-dessus.
a. Démontrer que arg·[(x +i)(y +i) / (1+i) ]=0 mod 2p.
En déduire que sous cette condition : x + y −xy +1 = 0.
arg·[(x +i)(y +i) / (1+i) ] = arg(z_B) +arg(z_C) -arg(z_A).
Or arg(z_B) +arg(z_C) =arg(z_A).
Donc arg·[(x +i)(y +i) / (1+i) ]=0 mod 2p.
(x +i)(y +i) / (1+i) =[xy +i²+i(x+y)] / (1+i)
[xy-1+i(x+y)](1-i) / 2 = [xy-1+x+y +i(x+y-xy+1)] / 2.
Or arg·[(x +i)(y +i) / (1+i) ]=0, donc x+y-xy+1 = 0.
b. Démontrer que si les deux conditions sont vérifiées et que de plus x diffère de1, alors :
y =(2x²+1)^½ et y = (x+1) / (x-1).
D'une part : y² = 2x² +1 soit y =(2x²+1)^½ ;
D'autre part : x+y-xy+1 = 0 ; y(1-x) +x+1) = 0 ; y= (x+1) / (x-1).
5. On définit les fonctions f et g sur l’intervalle ]1 ; +∞[ par :
f (x) =(2x²+1)^½ et g (x)= (x+1) / (x-1).
Déterminer le nombre de solutions du problème initial.
On pourra utiliser la fonction h définie sur l’intervalle ]1 ; +∞[ par h(x) = f (x)− g (x) et s’appuyer sur la copie d’écran d’un logiciel de calcul formel donnée ci-dessous.

Sur l’intervalle ]1 ; +∞[ :
la dérivée de f(x) est positive, f(x) est strictement croissante ;
la dérivée de g(x) est négative, la fonction g(x) est strictement décroissante.

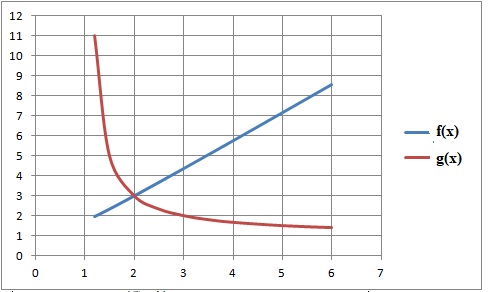
Le problème a une seule solution.

Nlle Calédonie.
On définit la suite de nombres complexes (z_n) de la manière suivante : z₀ = 1 et, pour tout entier naturel n,
z_n+1 =z_n / 3 +2i / 3.
On se place dans un plan muni d’un repère orthonormé direct.
Pour tout entier naturel n, on note A_n le point du plan d’affixe z_n.
Pour tout entier naturel n, on pose u_n = z_n − i et on note B_n le point d’affixe u_n.
On note C le point d’affixe i .
1. Exprimer u_n+1en fonction de u_n, pour tout entier naturel n.
u_n+1 = z_n+1 -i =z_n / 3 +2i / 3-i = z_n/3 -i / 3 = (z_n-i) / 3 = u_n / 3.
2. Démontrer que, pour tout entier naturel n,
u_n = (1 /3)ⁿ(1− i ).
u₀=1-i ; u_n+1 = u_n/ 3 ;
la suite (u_n) est géométrique de raison 1 / 3 et de premier terme 1-i.
Par suite u_n = (1-i)(1 / 3)ⁿ.
3. a. Pour tout entier naturel n, calculer, en fonction de n, le module de u_n.
|1-i| = (1² +(-1)²)^½ = 2^½.
Module de u_n : 2^½(1 / 3)ⁿ.
b. Démontrer que la limite en plus l'infini de |z_n-i| est égale à zéro.
-1 < 1 / 3 < +1, par suite (1/3)ⁿ tend vers zéro quand n tend vers plus l'infini.
c. Quelle interprétation géométrique peut-on donner de ce résultat ?

4. a. Soit n un entier naturel. déterminer un argument de u_n.
u_n / |u_n|= (1− i ) / 2^½ = cos ( -p /4) + i sin (-p/4) = exp(-ip/4).
-p/4 est un argument de u_n.
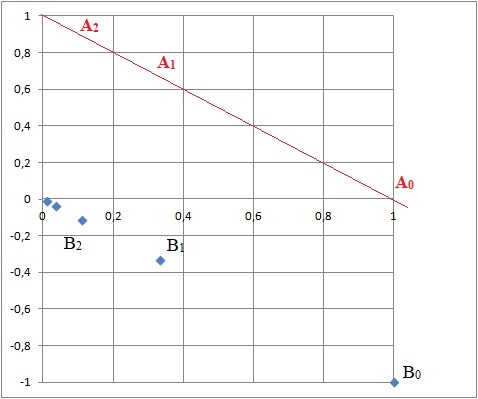
b. Démontrer que, lorsque n décrit l’ensemble des entiers naturels, les points B_n sont alignés.
u_n = 2^½(1 / 3)ⁿ exp(-ip/4) : B_n( 2^½(1 / 3)ⁿ ; - 2^½(1 / 3)ⁿ )
u_n+1 = 2^½(1 / 3)ⁿ⁺¹ exp(-ip/4). B_n+1( 2^½(1 / 3)ⁿ⁺¹ ; - 2^½(1 / 3)ⁿ⁺¹ ).

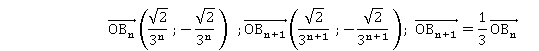
c. Démontrer que, pour tout entier naturel n, le point A_n appartient à la droite d’équation réduite : y = −x +1.
A₀( 1 ; 0) appartient à cette droite d'équation y = ax+b d'où b = -a
Equation de cette droite y = ax -a avec a réel.
z_n = u_n + i ; u_n = (1-i)(1 / 3)ⁿ ; z_n = 1 / 3ⁿ +i(1-1/3ⁿ).
z_n+1 = 1 / 3ⁿ⁺¹ +i(1-1/3ⁿ⁺¹).

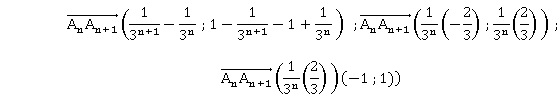
Le coefficient directeur de la droite cherchée est a = -1.
Par suite l'équation de cette droite est y = -x +1.

.
.

menu