Fonctions
logarithme et exponentielle, Concours Ecole de Santé des Armées
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
| .
. |
......
.....
|
2018.
QCM 1.
La fonction f définie sur R par
f(x) = ex+e-x est :
A. Croissante sur ] -oo ; 0[ et décroissante sur [0
; +oo[.
On dérive f
' (x) = ex-e-x= ex( 1-e-2x).
La dérivée
est du signe de 1- e-2x ; 1- e-2x > 0 si e-2x
< 1 soit x > 0.
B. Croissante sur R.
C. décroissante sur ]-oo ; 0[ et croissante sur [0
; +oo[. Vrai.
D.
décroissante sur ]-oo ; -2[ et croissante sur [-2 ; +oo[
QCM 2.
Soit f la fonction f définie sur R par f(x) = 5exp(0,2x2
+0,5x).
La tangente à la courbe représentative de la fonction f au point
d'abscisse zéro :
A. a pour équation
y = 2,5x +5. Vrai.
On dérive f ' (x) =5(0,4x+0,5)exp(0,2x2
+0,5x).
Coefficient de cette
tangente a = f '(0) = 2,5.
La tangente passe au
point de coordonnées ( 0 ; 5).
Equation de la tangente y
= 2,5 x +5.
B. a pour équation y = 5x+10.
C. a pour équation
y = 5x.
D.
est parallèle à l'axe des abscisses.
QCM 3.
Les solutions de l'inéquation ln(-x+5) < ln(x+1) sont :
A. ] 2 ; +oo[.
-x+5 et x+1doivent être
positifs : x < 5 et x > -1.
ln(-x+5) - ln(x+1) < 0
; ln[(-x+5) /(x+1)] < ln(1).
(-x+5) / (x+1) < 1 ; -x+5 < x+1 ; 2 x >4 ; x > 2.
B. ]-oo ; 5[.
C. ]-1 ; 5 [
D.
]2 ; 5[. Vrai.
QCM 9.
Soit la fonction g définie sur IR par g(x)=(3-2x)e-x . Une
primitive de la fonction g est la fonction G définie sur IR par :
A. G(x) =(3x-x2)e-x.
On dérive en posant u =
3x-x2 et v = e-x ; u' =3-2x ; v' = -e-x
; u'v +v'u =e-x(3-2x-3x+x2).
B.
G(x)
=(-3x+x2)e-x.
On dérive en posant u = -3x+x2
et v = e-x ; u' = -3+2x ; v' = -e-x ; u'v
+v'u =e-x(-3+2x+3x-x2).
C. G(x)
=(2x-1)e-x. Vrai.
On dérive en posant u = 2x-1 et v = e-x
; u' = 2 ; v' = -e-x ; u'v +v'u =e-x(2-2x+1).
D.
G(x)
=(5-2x)e-x.
On dérive en posant u = 5-2x et v = e-x
; u' = -2 ; v' = -e-x ; u'v +v'u =e-x(-2+2x-5).
QCM 10.
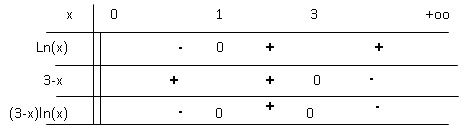
L’ensemble des solutions de l’inéquation ( 3-x) ln(x) > 0 sont :
A. [1 ; 3 ]. Vrai.
x doit être positif.
B. ]0
; 3 ]
C. ]
-oo ; 3 ]
D.
[1 ; +oo[.
QCM 11.
L'intégrale suivante est égale à :
A. 1.
B.
0,5.
C. e
/ (2(1+e)).
D.
ln[(1+e) / 2]. Vrai.
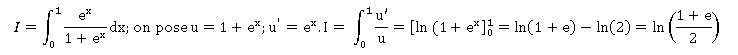
|
...
|
|
2015.
QCM 4.L’équation : exp(x2−2x) =1 / e admet, dans R, pour ensemble de solutions :
A. aucune solution;
B. {1} vrai.
C. {1 ; 2}
D. {0 ; 2}
x2−2x = -1 ; x2−2x +1=0 ; (x-1)2 = 0 ; x = 1.
QCM 5 :
L’inéquation : exp(1−x /5) >1 admet, dans R, pour ensemble de solutions :
A. ]−∞; 5[ vrai.
B. ]0 ; 5[
C. ]−∞; 0[
D. ]1/5 ; +∞[
Par croissance de la fonction logarithme népérien :
1-x / 5 > ln (1) ; 1-x / 5 >0 ; x / 5 <1 ; x <5.
QCM 6 :
La limite de x2 −x ln(x) quand x tend vers +∞ vaut :
A. −∞
B. +∞ vrai.
C. 0
D. n’existe pas.
x2 (1-ln(x) / x ).
Au voisinage de l'infini : ln(x) / x tend vers zéro ; 1-ln(x) / x tend vers 1.
Par produit des limites x2 (1-ln(x) / x ) tend vers l'infini.
QCM 7 :
Le nombre de solutions de l’équation définie sur R+* : 2(lnx)2 +3lnx −5 = 0 est :
A. 0
B. 1
C. 2, vrai.
D. 3
On pose X = ln(x) ; 2X2+3X-5 = 0 ; discriminant D = 32+4 x2x5 =49 ; D½ = 7.
X1 = (-3 +7) / 4 = 1 soit x = e.
X1 = (-3 -7) / 4 = -2,5 soit x = e-2,5.
QCM 8 :
La fonction h définie sur R par h(x) = ln(4+x2) est dérivable sur R.
Sa dérivée est la fonction h′ définie sur R par h′(x) =
A. 1/(4+x2)
B. −2x/(4+x2)
C. x/(4+x2)
D. 2x/(4+x2). Vrai.
On pose u =4+x2 ; u' = 2x ; h'(x) = u' / u = 2x/(4+x2).
QCM 9 : Une primitive de la fonction f définie sur ]0 ; +∞[ par f (x) =2 /x +e3x est :
A. F(x)= 2ln(3x)+1/3 e3x. Vrai.
On dérive F(x) : 2 x3 /(3x)+3 / 3e3x= f(x).
B. F(x)= −2 /x2 +3e3x. C'est la dérivée de f(x)
C. F(x) = 2ln(3x)+3e3x. 3e3xest la dérivée de e3x.
D. F(x)= 2ln(x)+3e2x. L'exposant de l'exponentielle diffère de trois.
|
....
|
2014.
QCM 1 :
Soit la fonction h définie pour out réel x par h(x) = e−x −x +4. Soit C la courbe représentative de h. :
A. h'(x) =e-x-1. Faux.
h'(x) = -e-x-1=-(e-x+1), toujours négative ; h(x) est strictement décroissante.
B. h admet un maximum.
Faux.
C. C admet une asymptote horizontale. Faux.
Au voisinage de +oo, le terme en exponentielle tend vers zéro ; h(x) tend vers -oo.
Au voisinage de -oo, le terme en exponentielle l'emporte sur -x+4 et h(x) tend vers +oo..
D. L'équation h(x) =5 a une solution unique dans l'ensemble des réels. Vrai.
h(x) strictement décroissante et h(x) décrit R.
QCM 2 :
Dans l’ensemble des nombres réels, l’inéquation −2xe−x+1 > 0 a pour ensemble de solutions :
A. aucune.
Le terme en exponentielle est positif.
-2x est positif ou nul pour x appartenant à ]-oo ; 0].
B. { 0 }
C. ]-oo ; 0 ]. Vrai.
D. [0 ; +oo[.
QCM 3 :
On considère l'intégrale I suivante.
On pourra, pour calculer I , utiliser la dérivée de la fonction h définie sur [1 ; e] par h(t ) = t3[3ln(t )−1].
La valeur exacte de I est :
Calcul de h'(x) : on pose u = t3 et v = 3 ln(t)-1 ; u' = 3t2 ; v' = 3 /t.
u'v+v'u =3t2(3ln(t)-1) +3t2=9t2ln(t).
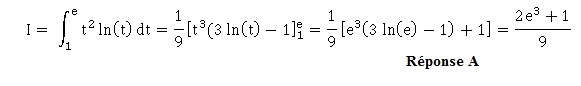
|
|