Fonctions logarithme et exponentielle, Concours puissance alpha.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

......


.....

  2015.
8. Fonction exponentielle
Soit F1 et g les fonctions définies sur R respectivement par F1(x) = e−x −2x et g (x)= e−x (x +1) / (e−x +2).
On désigne par (C) la courbe représentative de la fonction F1 et par (xn) la suite définie, pour tout n entier, par x0 = 1 et xn+1 = g (xn).

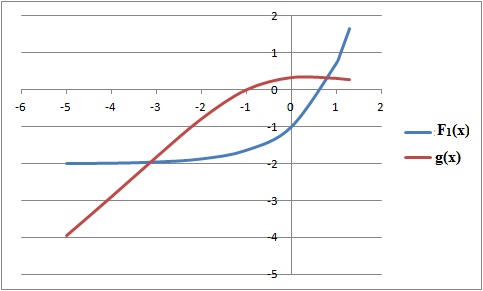a) L’équation F1(x) = 0 admet une unique solution α avec 0 < α < 1. Vrai.
Dans les questions b., c. et d., on admet la convergence de la suite (xn).
b) La limite de xn  est égale à a quand x tend vers l'infini. Faux.
g (x)=  (x +1) / (1+2ex). g() est équivalent à x / (2ex) quand x tend vers l'infini. Par croissance comparée, g(x) tend vers zéro quand x tend vers l'infini.
c) Si a est réel, alors la tangente à (C) en x = a coupe l’axe des abscisses en un point d’abscisse g (a). Vrai.
F '1(x) = -e-x-2 ; coefficient directeur de la tangente à C au point d'abscisse x=a : -e-a-2.
La tangente passe par le point A( a ; e-a-2a) ;
Equation de cette tangente : e-a-2a = (-e-a-2)a+b  ; b = (1+a)e-a  ; y =(-e-a-2)x+ (1+a)e-a  ;
La tangente coupe l'axe des abscisses au point de coordonnées  (   (1+a)e-a / (e-a+2) ; 0).

9. Fonction exponentielle et logarithme.
Soit f la fonction définie sur ]0 ; +oo[ par f (x) =ln(e2x −1) / ex , g la fonction définie sur ]1 ; +oo[ par g (x) = 2x−(x−1)×ln(x−1) et F la fonction définie sur ]1 ; +∞[ par f(x)=ln(x2 −1) / x.
.
a. g'(x) = 1+ln(1 / (x-1)). Faux.
On pose u = (x-1); v = ln(x-1) ; u'=1 ; v' = 1/(x-1) ; u'v+v'u = ln(x-1) +1 ; g'(x) = 2-(ln(x-1)+1).
b. f '(x) = g(x2) / x2. Faux.
On pose u = ln(x2 −1) ; v = x ; u' = 2x/(x2 −1) ; v' = 1 ; (u'v-v'u) / v2 =[2x2 /(x2 −1) - ln(x2 −1) ] / x2 .
c. g admet un minimum en x = e+1. Faux.
g'(x) = 0 pour x = e+1.
g'(x) est négative pour x > e+1 ; g(x) est décroissante  pour x > e+1.



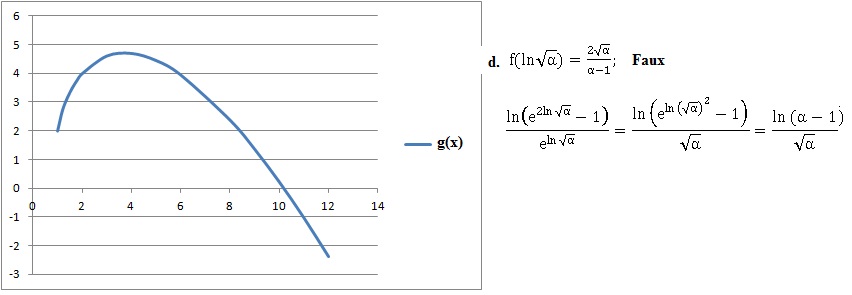
2017.
Exercice 6. Etude de 2 fonctions.
Soient f et g deux fonctions définies par f(x) = ln(2x) et g(x) = ln(x2-1) de courbes représentative respectives Cf et Cg.
a. g(0,5) <0. Faux.
g (x) n'est pas définie sur ]-1 ; +1 [
b. g'(x) =1/(x2-1)  Faux.
On pose u = x2-1 ; u' = 2x ; g'(x) = u' / u = 2x /(x2-1).
c. La tangente à Cg en x = 2½ a pour équation y = 2 x2½x-4. Vrai.
g'(2½)=2 x2½; la tangente passe au point de coordonnées ( 2½ ; 0) ;
équation de la tangente : y = 2 x2½x +b ; 0 = 4+b ; b = -4.
d. Si x appartient à ]1 ; 1+2½], la courbe Cg est au dessus de Cf. Faux.


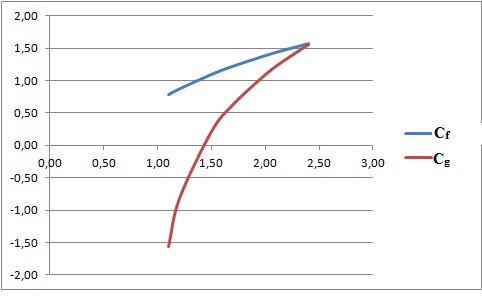
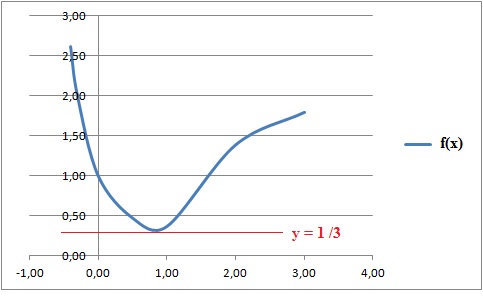
Exercice 7. Etude d'une fonction exponentielle.
Soit fla fonction définie sur R par f(x) = exp(x2-2x).
a. f(1) =-1/e. Faux.
f(1) = exp(12-2) = e-1 = 1 /e.
b. La limite de f(x) en moins l'infini est égale à la limite de f(x) en plus l'infini. Vrai.

c.f '(x) = f(x). Faux.
f '(x) = (2x-2) exp(x2-2x).
d. L'équation f(x) = 1 /3 admet deux solutions dans R. Faux.
ln(1/3) = -ln3  = x2-2x ; x2-2x +ln 3 = 0 ; D  = 4-4 ln3 <0.



...

2018.
Exercice 12. Etude d’une fonction logarithme.
On considère la fonction f définie par : ⨍(x) = ln(1 − x2).
On note D l’ensemble de définition de f.
a) 1 – x2> ” 0 si et seulement si –1 <• x <• 1. Vrai
b) D = [−1;1].  Faux.
D = ]-1 ; 1 [.
c) La fonction f a pour fonction dérivée la fonction f ’ définie sur D par f ’(x) =1 / (1-x2). Faux.
On pose u = 1-x2 ; u' = -2x ; f '(x) = -2x /(1-x2).
d) L’équation f(x) = 1 a pour solutions x = (e−1)½ et x = −(e−1)½.  Faux.
(e−1)½ et  −(e−1)½ n'appartiennent pas à D.
Exercice 13. Etude d’une fonction exponentielle.
Soit f la fonction définie par ⨍(x)= e2x /(x2+1). On désigne par C la courbe représentative de f dans un repère orthonormal du plan.
a) Quand x tend vers moins l'infini, f(x) tend vers moins l'infini. Faux.
Le terme e2x tend vers séro et (x2+1) tend vers plus l'infini. t(x) tend donc vers zéro.
b) Quand x tend vers plus l'infini, f(x) tend vers plus l'infini. Vrai.
Le terme e2x croît plus vite que le polynöme x2+1, au voisinage de plus l'infini..
c) La fonction f a pour fonction dérivée la fonction f ’ définie sur R par f ’(x) =2(x2-x+1) / (e-x(x2+1)) . Faux.
On pose u = e2x et v = x2+1 ; u' = 2e2x ; v' = 2x.
(u'v -v'u) / v2 =( 2e2x(x2+1)-2xe2x) / (x2+1)2=2e2x(x2+1-x) /(x2+1)2.
d) f est croissante sur ]−oo €; 0] et décroissante sur [0;€+oo[. Faux.
La dérivée est du signe de x2-x+1, polynome positif quel que soit la valeur de x.

 2014.
Exercice 12. Etude  d'une fonction logarithme.
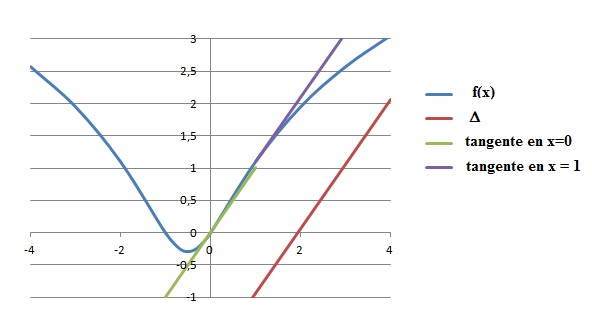
On considère la fonction f définie sur R par f (x) = ln(x2 +x +1) de courbe représentative (C ).
a. f est croissante sur R. Faux.
f '(x) = (2x+1) / (x2 +x +1).
Si x < - 0,5, f '(x) est négative et f(x) est strictement décroissante.
Si x > - 0,5, f '(x) est positive et f(x) est strictement croissante.
Si x = -0,5, f '(x) est nulle et f(x) admet un minimum égal à : f(-0,5) = ln(0,25 -0,5 +1) = ln (0,75).
 b. (C ) admet une unique asymptote verticale. Faux.
c. Pour tout x réel, f (x)>ln(3/4). Vrai.
d. Il existe deux points de (C ) ayant une tangente à (C ) parallèle à la droite (Δ) d’équation y = x −ln7. Vrai.
Le coefficient directeur des tangentes doit être égal à 1.
 f '(x) = (2x+1) / (x2 +x +1) = 1 ; 2x+1 = x2 +x +1 ; x2 -x  = 0 soit x = 0 et x = 1.


13. Etude d'une fonction exponentielle.
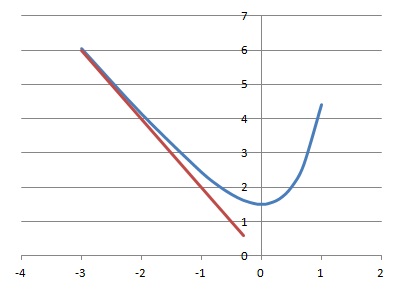
Soit f la fonction définie sur R par f (x) =0,5 e2x+ex-2x
On désigne par C sa représentation graphique dans un repère orthonormé du plan.
a. Pour tout réel x, on a : f ′(x) = (ex −1) (ex +2). Faux.
f '(x) =ex+ex-2 = 2(ex-1).
f '(x) est négative si  x <0 et f(x) est strictement décroissante.
f '(x) >0 si x >0 et f(x) est strictement croissante.
f '(x) = 0 si x=0 et f(x) présente un minimum égal  à f(0) = 1,5.
b. Pour tout réel x, on a : f (x) >1,5. Faux, il faudrait écrire f(x) >1,5.
c. C admet l’axe des abscisses comme asymptote horizontale en +oo. Faux.
d. Quand x tend vers -oo, f(x) tend vers + oo. Vrai.
Au voisnage de -oo, les termes en exponentielle sont nuls et f(x) est équivalente  à -2x.
....

 2012.
Exercice 1.
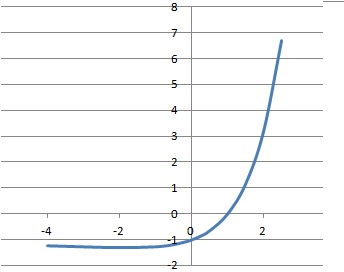
Soit la fonction f définie sur R* par f(x) =(1-x)(1-ex) / x.
a. Quand x tend vers zéro, f(x) tend vers zéro. Faux.
Au voisinage de zéro, f(x) est équivalente à (1-ex) / x.
1-ex équivalent à 1 -(1+x+x2/2) =-x-x2/2.
(1-ex) / x est équivalent à -1.
 b. Quand x tend vers moins l'infini, la limite de f(x) est 1. Faux.
Au voisinage de -oo, le terme ex est nul ; f(x) est équivalente à -x / x =-1.
c. On appelle g la fonction définie sur R par: g(x) = f (x) si x diffère de zéro  et g(0) = –1.
La fonction g est continue sur R. Vrai.

d. Quand x tend vers plus l'infini, la limite de (n-1)(1-exp(1/n)) est égale à -1. Vrai.
On pose x = 1/n ; au voisinage de zéro, 1-ex équivalent à 1 -(1+x+x2/2) =-x-x2/2.
1/x-1 est équivalent à 1/x ; (n-1)(1-exp(1/n)) est équivalent à -1.

Exercice 2 .
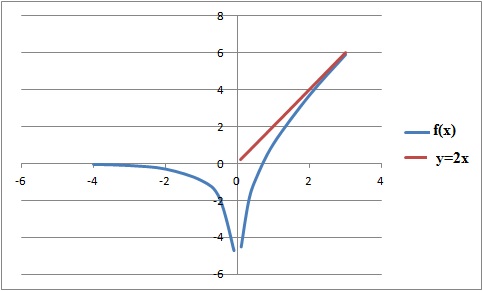
  Soit f la fonction définie par f (x) = ln(e2x – 2ex + 1).
a. L'ensemble de définition de f est R. Faux.
e2x – 2ex + 1 = (ex-1)2, toujours positif ou nul ( si x = 0).
f(x) n'est pas définie en 0.
 b. On a: f (x) < 0 si et seulement si x < 0. Faux.
f(0,1) =2 ln(e0,1-1)= -4,5 .
c. Pour tout x de R*, on peut écrire f (x) = 2ln(ex – 1). Faux.
f (x) = 2ln |ex – 1|
d. La courbe représentant f dans un repère orthonormal du plan possède pour asymptotes les axes du repère et la droite d'équation y = 2x. Vrai.
.
 


.


  

menu