Mathématiques,
bac S Nlle Calédonie 03 / 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
.
|
|
Exercice 1. ( 5 points)
Partie A.
Une société de location de voitures s’intéresse à l’état mécanique de
son parc automobile afin d’anticiper les frais d’entretien.
On dispose des données suivantes :
• 20% des voitures sont sous garantie;
• pour 1% des voitures sous garantie, une réparation est nécessaire;
• pour 10% de celles qui ne sont plus sous garantie, une réparation est nécessaire.
On choisit une voiture au hasard dans le parc et on considère les évènements suivants :
• G : « la voiture est sous garantie » ;
• R : « une réparation est nécessaire ».
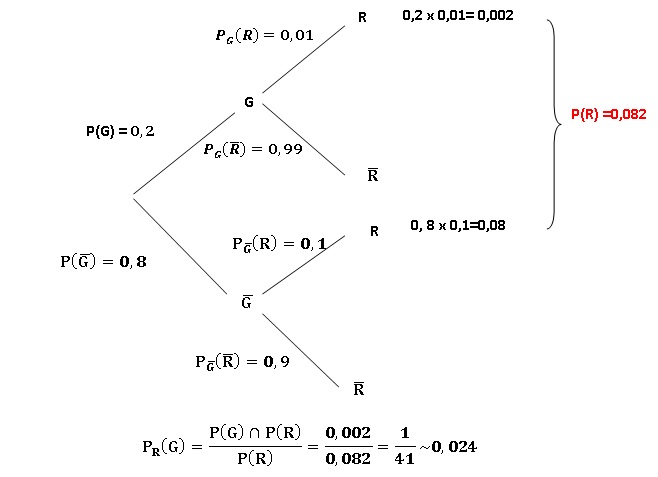
1. a. Traduire la situation par un arbre pondéré.
b. Calculer la probabilité que la voiture choisie soit sous garantie et nécessite une réparation.
c. Justifier que P(R) = 0,082.
d. Il s’avère que la voiture choisie nécessite une réparation.
Quelle est la probabilité qu’elle soit sous garantie ? On arrondira le résultat à 10−3.
2. La société de location fait appel à un garage pour l’entretien de son parc automobile.
L’entretien consiste en une révision à laquelle s’ajoutent
d’éventuelles réparations. Les conditions commerciales du garage sont
les suivantes :
• si la voiture est encore sous garantie, l’entretien est gratuit ;
• si la voiture n’est plus sous garantie, l’entretien est facturé de la
manière suivante : la révision coûte 100 € et, si une réparation est
nécessaire, il faut rajouter 400 €.
Sachant que son parc automobile compte 2 500 voitures, est-il
raisonnable pour la société de location de prévoir un budget annuel de
250 000 euros pour l’entretien de l’ensemble des voitures ?
On pourra introduire la variable aléatoire X qui représente le coût d’entretien d’une voiture.
Nombre de voitures qui ne sont plus sous garantie : 0,8 x2500 =2000.
Coût de l'entretien : 2000 x 100 = 200 000 €.
Nombre de voitures à réparer : 500 x0,01 + 2000 x0,10 =205.
Coût des réparations : 205 x400 =82 000 €.
Total : 282 000 €, le budget est insuffisant.
Partie B.
La société de location propose à ses clients deux contrats de location
: un contrat de courte durée (inférieure à 2 jours) et un contrat de
longue durée (de 3 à 7 jours). La directrice de cette société affirme
que 80% des clients demandent un contrat de courte durée.
Sur les 600 derniers contrats signés l’année précédente, 550 étaient des contrats de courte durée.
1. En supposant que
l’affirmation de la directrice est correcte, déterminer un intervalle
de fluctuation asymptotique au seuil de 95% de la fréquence des
contrats de courte durée.
2. Que peut-on penser de l’affirmation de la directrice ?
1,96 [p(1-p) / n ]½ =1,96 (0,8 x0,2 / 600)½ =0,032.
Intervalle de fluctuation asymptotique [ 0,8-0,032 ; 0,8 +0,032 ] soit [0,768 ; 0,832 ].
550 / 600 = 0,917.
0,917 est en dehors de cet intervalle. Au risque de 5 %, l'affirmation
de la directrice est fausse. 91 % des clients demandent un contrat de
courte durée.
Partie C.
On modélise le nombre de kilomètres parcourus par les clients louant
une voiture pour une semaine par une variable aléatoire Y suivant la
loi normale d’espérance μ = 450 et d’écart-type σ = 100.
1. Quelle est la probabilité que le client louant la voiture pour une semaine roule entre 500 km et 600 km?
On arrondira le résultat à 10−3.
P( Y < 500) =0,69146 ; P( Y < 600) =0,93319 ;
P ( 500 < Y < 600) =0,93319-0,69146 ~0,242.
2.
La société de location souhaite faire une offre promotionnelle aux 15%
de ses clients parcourant le moins de kilomètres en une semaine.
En-dessous de quel kilométrage hebdomadaire, arrondi à l’unité, un
client sera-t-il concerné par cette offre ?
P(Y < 347) ~0,149.
|
|
|
Exercice 2. 6 points.
Partie A : Étude d’une fonction auxiliaire
Soit g la fonction définie sur R par
g (x) = (x +2)ex−4 −2.
1. Déterminer la limite de g en +∞.
Quand x tend vers plus l'infini :
x+2 tend vers plus l'infini ; ex-4 tend vers plus l'infini.
Par produit des limites, g(x) tend vers plus l'infini.
2. Démontrer que la limite de g en −∞vaut −2.
Quand x tend vers moins l'infini :
x+2 tend vers moins l'infini ; ex-4 tend vers zéro.
Par produit des limites, (x +2)ex−4 tend vers zéro et g(x) tend vers -2.
3. On admet que la fonction g est dérivable sur R et on note g ′ sa dérivée.
Calculer g ′(x) pour tout réel x puis dresser le tableau de variations de g .
On pose u = x+2 ; v = ex-4 ; u' = 1 ; v' = ex-4.
u'v + v'u = ex-4 +(x+2)ex-4 = ex-4(x+3).
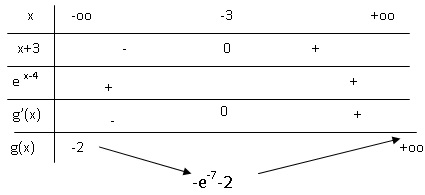
4. Démontrer que l’équation g (x) = 0 admet une unique solution α sur R.
Sur ]-oo ; -3[, g(x) est strictement décroissante de -2 à -e-7-2 ; pas de solution sur cet intervalle.
sur ]-3 ; +oo[, g(x) est continue ( car dérivable) et strictement croissante de e-7-2 à +oo.
g(x) = 0 admet une solution unique sur R.
5. En déduire le signe de la fonction g sur R.
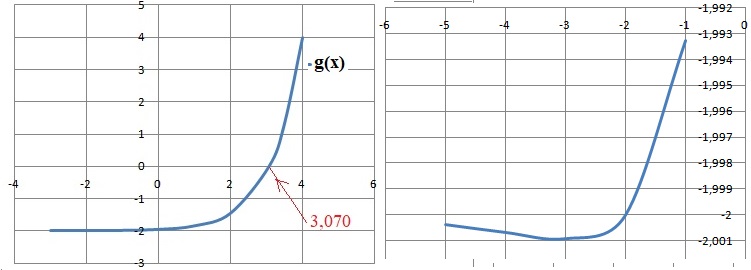
Sur ]-oo ; 3,070[ g(x) est strictement négative ; g(3,070) = 0 ; sur ]3,070 ; +oo(, g(x) est strictement positive.
6. À l’aide de la calculatrice, donner un encadrement d’amplitude 10−3 de α.
Partie B : Étude de la fonction f
Soit f la fonction définie sur R par f (x) = x2 −x2ex−4.
1. Résoudre l’équation f (x) = 0 sur R.
x2(1-ex-4) = 0 ; x= 0 et ex-4 = 1 ; x-4 = 0 soit x = 4.
2. On admet que la fonction f est dérivable sur R et on note f ′ sa fonction dérivée.
On admet par ailleurs que, pour tout réel x, f ′(x) = −xg (x) où la fonction g est celle définie à la partie A.
Étudier les variations de la fonction f sur R.
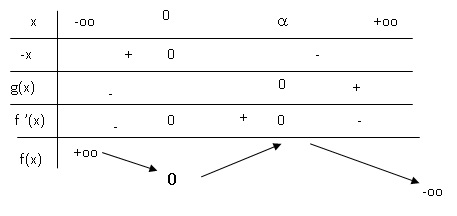
3. Démontrer que le maximum de la fonction f sur [0 ; +∞[ est égal à α3/(α+2).
g(a) = 0 = (a+2)ea-4-2 = 0 ; ea-4= 2 /(a+2).
f(a) =a2(1-ea-4)=a2(1-2 /(a+2))=α3/(α+2).
.
.
Partie C : Aire d’un domaine
Dans un repère orthonormé, on noteD le domaine compris entre la courbe représentative Cf de la fonction f , la parabole P d’équation y = x2 et les droites d’équations x = 0 et x = 4.
1. Déterminer la position relative des courbes Cf et P .
f(x)-y = -x2ex-4 < 0.
La parabole est au dessus de la courbe Cf.
2. On admet qu’une primitive de la fonction f sur R est définie par :
F(x) =x3 /3 −(x2 −2x +2)ex−4.
Calculer l’aire du domaine D en unité d’aire. On donnera la valeur exacte.
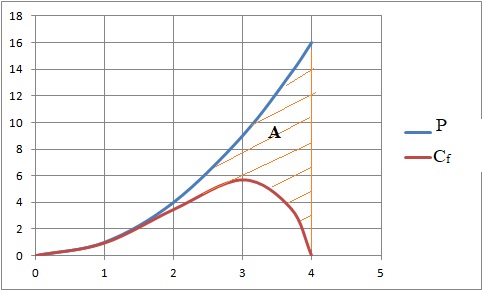
Aire comprise entre P, l'axe des x et les droites d'équation x=0 et x = 4.
A1= [x3 / 3]04 =43 /3 -0=43 /3.
Aire comprise entre Cf, l'axe des x et les droites d'équation x=0 et x = 4.
A2=F(4) - F(0)=43 /3 -(42-8+2) -(-2e-4)=43 /3 -10 +2e-4.
A = A1-A2 = 10 -2e-4.
|
|
|
|
Exercice 3. 4 points
Commun à tous les candidats
Pour chacune des quatre affirmations suivantes, indiquer si elle est vraie ou fausse et justifier la réponse choisie.
Pour les questions 1 à 3, on se place dans un plan muni du repère orthonormé direct.
1. Soit (E) l’équation d’inconnue le nombre complexe z
z (z2 −8z +32) = 0.
Affirmation 1
: Les points dont les affixes sont les solutions de l’équation (E) sont
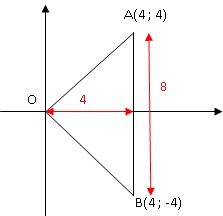
les sommets d’un triangle d’aire égale à 16 unités d’aire. Vrai.
Solutions de (E) : z =0 ( origine) ;
et z2 −8z +32 = 0 ; discriminant D = (-8)2 -4 x32 = -64 = 64 i2 ;
Solutions : (8 +8 i) / 2 = 4 +4i ( affixe du point A) et 4-4i( affixe
du point B, symétrique de A par rapport à l'axe des réels).
2. Soit E l’ensemble des points dont les affixes z vérifient |z −3| = |z +3|.
Affirmation 2 : L’ensemble E est le cercle de centre O et de rayon 3. Faux.
Point M d'affixe M ; point A d'affixe 3 ; point B d'affixe -3
|z −3| = |z +3| est équivalent à |zM-zA| = |zM-zB | soit AM = BM.
M appartient à la médiatrice du segment (AB].
3. On considère la suite de nombres complexes (zn) définie pour tout entier naturel n par : zn = (1-i 3½)n.
Pour tout entier naturel n, on note Mn le point d’affixe zn.
Affirmation 3 : Pour tout entier naturel n, les points Mn O et Mn+3 sont alignés. Vrai.
|z1|=(1 +3)½ = 2 ; z1/ |z1| =0,5 -0,5 i 3½ = exp(-ip/3).
z1 = 2 exp(-ip/3) ; zn = 2nexp(-i n p/3). zn+3 = 2n+3exp(-i (n p/3 + p)).
4. On considère l’équation d’inconnue le nombre réel x : sin(x) (2cos2(x)−1) = 0.
Affirmation 4 : Cette équation admet exactement quatre solutions sur l’intervalle ]−π ; π] qui sont : −π/4 ; 0; π/4 et π. Faux.
sin (x) = 0 ; x =0 ; x = p.
cos2(x)= 0,5 ; cos (x) = 2 / 2½ ; x = ± p / 4 ; cos (x) = -2 / 2½ ; x = ±3 p / 4.
|
|
Exercice 4. 5 points.
On considère la suite (un) à valeurs réelles définie par u0 = 1 et, pour tout entier naturel n,
un+1 =un/ (un +8)
.
Partie A : Conjectures
Les premières valeurs de la suite (un) ont été calculées à l’aide d’un tableur dont voici une capture d’écran :
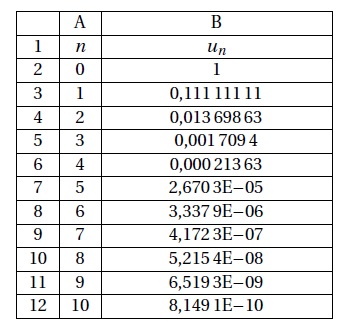
1. Quelle formule
peut-on entrer dans la cellule B3 et copier vers le bas pour obtenir
les valeurs des premiers termes de la suite (un) ?
=B2/(B2+8)
2. Quelle conjecture peut-on faire sur les variations de la suite (un) ?
La suite est décroissante.
3. Quelle conjecture peut-on faire sur la limite de la suite (un) ?
La suite tend vers zéro.
4. Écrire un algorithme calculant u30.
Variable n entier, x réel.
x = 1
Pour n =1 à 30 faire :
x = x/(x+8).
Fin Pour
Afficher x.
Partie B. Etude générale.
1. Démontrer par récurrence que, pour tout entier naturel n, un > 0.
Initialisation : u0 = 1, la proposition est vraie au rang zéro.
Hérédité : on supose un >0.
un+1 = un / (un+8 ) est donc positif.
Conclusion : la propriété est vraie au rang zéro et héréditaire. Elle est vrai pour tout n.
2. Étudier les variations de la suite (un).
un+1-un = un / (un+8 ) -un =( - u2n -7 un)/ (un+8 ) est négatif.
un+1< un , la suite est décroissante.
Quand n tend vers l'infini, un tend vers zéro.
3. La suite (un) est-elle convergente ? Justifier.
La suite est décroissante et minorée, donc elle converge.
Partie C : Recherche d’une expression du terme général
On définit la suite (vn) en posant, pour tout entier naturel n,
vn = 1+7 / un.
1. Démontrer que la suite (vn) est une suite géométrique de raison 8 dont on déterminera le premier terme.
vn+1 =1 + 7 / un+1 = 1 + 7 (8+un) / un = 8+56/un =8(1+7/un)=8 vn.
(vn) est une suite géométrique de raison 8 et de premier terme v0 = 8.
2. Justifier que, pour tout entier naturel n, un =7 /(8n+1 −1).
vn = 8n+1 ; un =7 /(vn-1) = 7 /(8n+1 −1).
3. Déterminer la limite de la suite (un).
Quand n tend vers plus l'infini : 8 n+1 tend vers plus l'infini ; 8n+1 −1 tend vers plus l'infini et 7 / (8n+1 −1) tend vers zéro.
4. On cherche dans cette question le plus petit entier naturel n0 tel que, pour tout entier naturel n supérieur ou égal à n0, un < 10−18.
Justifier l’existence d’un tel entier n0 et déterminer sa valeur.
7 /(8n+1 −1) < 10−18 ; 7 1018 < 8n+1-1 ; 7 1018 +1< 8n+1.
log( 7 1018 +1) < (n+1) log (8) ; n+1 > log( 7 1018 +1) / log(8) ;
n0 > log( 7 1018 +1) / log(8) -1 ; n0 > 20.
|
|