Mathématiques,
bac St2S Métropole 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
Exercice 1 ( 5 points).
Un médicament est prescrit sous forme d’injections qui doivent être administrées une fois par semaine.
Le volume de la première dose est déterminé en fonction de la masse
corporelle du patient à raison de 2 mL de médicament par kg. Chaque
semaine, le volume de la dose administrée est augmenté de 5 %. Dès que
le volume de la dose administrée est supérieur ou égal au double du
volume initial, on interrompt le traitement après cette dernière
injection.
On applique le traitement à une personne dont la masse corporelle est de 60 kg.
Pour déterminer les doses administrées, on s’aide de la feuille de
calcul automatisé ci-dessous (les cellules de la plage [B2 : G2] sont
paramétrées pour afficher les valeurs arrondies au dixième).
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
1
|
Numéro de l'injection
|
1
|
2
|
3
|
4
|
5
|
6
|
2
|
Dose administrée ( mL) à chaque injection
|
120
|
126
|
132.3
|
138,9
|
145,9
|
153,2
|
Tous les résultats seront arrondis au dixième.
1) Justifier les résultats obtenus dans les cellules B2 et C2.
2 mL de médicament par kg : 2 x 60 = 120 mL
Chaque semaine, le volume de la dose administrée est augmenté de 5 %.
120 x1,05 =126 mL.
2)
Quelle formule peut-on saisir dans la cellule C2 qui, recopiée vers la
droite, permet de calculer les valeurs des doses à administrer chaque
semaine ?
=B2*1,05
3) On appelle Vn la valeur, en mL, du volume de la dose administrée lors de la n-ième injection.
Ainsi, V1= 120.
a) Justifier que la suite (Vn) est géométrique et préciser sa raison.
On passe d'un terme au suivant en le multipliant par 1,05. La raison est égale à 1,05.
Le premier terme est égal à V1 = 120.
b) Pour tout entier naturel n, exprimer Vn en fonction de n.
Vn = 120 x 1,05n-1.
c) Calculer le volume administré lors de la 10e injection.
V10 = 120 x1,059=186,2 mL.
4) a) Expliquer
pourquoi le nombre total d’injections administrées lors du traitement
peut s’obtenir en résolvant l’inéquation d’inconnue , entier naturel :
120 x1,05n-1 > 240.
Dès
que le volume de la dose administrée est supérieur ou égal au double du
volume initial, on interrompt le traitement après cette dernière
injection.
b) Justifier que le traitement comporte au total 16 injections.
120 x 1,0515 = 249,5, valeur supérieure à 240.
5) Déterminer le volume total de médicament administré au patient lors de l’ensemble du traitement. Arrondir au dixième de mL.
V1 ( 1-qn) / (1-q) =120 ( 1-1,0516) / (1-1,05) = 120 x1,079 / 0,05 = 2838,9 mL.
|
|
|
Exercice 2 ( 8 points ).
Les parties A et B sont indépendantes
Partie A : Lien entre le prix du tabac et la consommation de cigarettes en France
Le tableau ci-dessous présente l’évolution du prix en euros du paquet
de 20 cigarettes de la marque la plus vendue en France ainsi que celle
du nombre total de paquets de 20 cigarettes vendus en France, exprimé
en milliards et arrondi au centième.
Année
|
2004
|
2007
|
2010
|
2013
|
2016
|
Prix du paquet ( xi)
|
5
|
5,13
|
5,65
|
6,7
|
7
|
Nombre total de paquets ( yi) en milliards
|
2,75
|
2,75
|
2,74
|
2,38
|
2,25
|
1)
Déterminer la baisse en pourcentage, arrondie à 0,1 %, du nombre total
de paquets de 20 cigarettes vendus en France entre l’année 2004 et
l’année 2016.
(2,25 -2,75) / 2,75 x100 = -18,2 %.
2) En annexe, à
rendre avec la copie, figurent quatre des cinq points du nuage
représentant les données du tableau. Compléter le nuage de points.
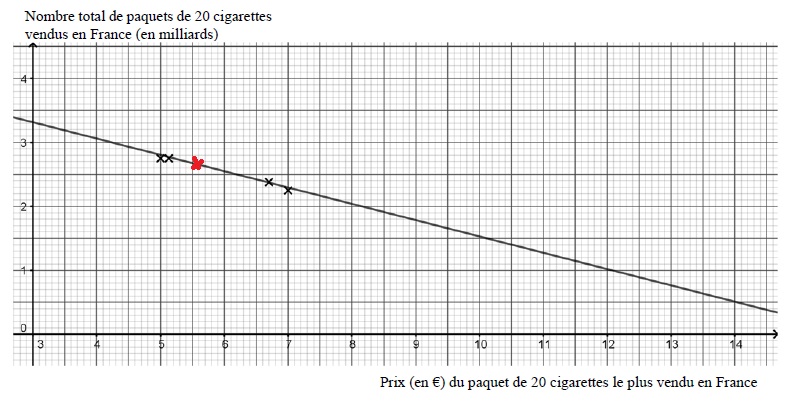
3) On choisit comme droite d’ajustement du nuage de points la droite (d) d’équation :
y = -0,255 x +4,08
représentée en annexe. On suppose qu’elle modélise le nombre total de
paquets de 20 cigarettes vendus en France en fonction du prix d’un
paquet de 20 cigarettes de la marque la plus vendue en France.
a) Le ministère de
la santé souhaite que le prix de vente d’un paquet de 20 cigarettes de
la marque la plus vendue soit de 10 € en 2020. Estimer, selon le modèle
proposé, le nombre total de paquets de 20 cigarettes qui seront vendus
en 2020.
y = -0,255 x10 +4,08 = 1,53 €.
b) Déterminer le
prix minimum d’un paquet de 20 cigarettes de la marque la plus vendue
qui, selon le modèle proposé, permettrait de passer sous la barre d’un
milliard le nombre total de paquets de 20 cigarettes vendus. Préciser
la méthode employée.
-0,255 x +4,08 < 1 ;
0,255 x -4,08 > -1 ;
0,255 x > 4,08-1 ;
x > 3,08 / 0,255 ; x >12,08.
Partie B : Consommation de tabac et revenus en France
Dans cette partie, tous les résultats seront arrondis au millième.
1) En 2000, une
enquête réalisée auprès de 10 508 personnes âgées de 18 à 75 ans a
étudié la relation entre le tabagisme et les revenus. Les revenus sont
répartis en trois tranches. Les résultats de l’enquête figurent dans le
tableau suivant :
|
Revenus inférieurs
|
Revenus moyens
|
Revenus supérieurs
|
Total
|
Fumeurs
|
1126
|
1155
|
914
|
3195
|
Non fumeurs
|
2403
|
2596
|
2314
|
7313
|
Total
|
3529
|
3751
|
3228
|
10508
|
On choisit au hasard la fiche réponse d’un individu ayant participé à l’enquête.
On définit les événements suivants :
F : « la fiche est celle d’un fumeur » ;
I : « la fiche est celle d’un individu dont les revenus sont dans la tranche des revenus inférieurs » ;
M : « la fiche est celle d’un individu dont les revenus sont dans la tranche des revenus moyens » ;
S : « la fiche est celle d’un individu dont les revenus sont dans la tranche des revenus supérieurs ».
a) Calculer la probabilité que la fiche choisie soit celle d’un individu aux revenus moyens.
P(M) = 3751 / 10508 = 0,357.
b) Calculer F ∩ M et interpréter ce résultat dans le contexte de l’exercice.
P(F ∩ M) =1155 / 10508 =0,110.
La probabilité qu'un individu soit fumeur en ayant des revenus moyens est égale à 0,110.
c) Sachant que la fiche choisie est celle d’un individu aux revenus moyens, déterminer la probabilité qu’il s’agisse d’un fumeur.
PM(F) = P(F ∩ M) /P(M) =0,110 / 0,357 = 0,308.
d) On admet que PI(M) ~ 0,319 et PS(F) ~ 0,283.
Interpréter ces résultats dans le contexte de l’exercice.
La probabilité qu'un individu ayant des revenus inférieurs soit fumeur est égale à 0,319.
La probabilité qu'un individu ayant des revenus supérieurs soit fumeur est égale à 0,283.
En 2000 on rencontre le moins de fumeurs parmi les individus ayant des revenus supérieurs.
2) Une enquête
semblable a été effectuée en 2016. Elle a permis d’obtenir l’arbre de
probabilités suivant qui utilise les mêmes notations d’événements qu’à
la question 1) de la Partie B.
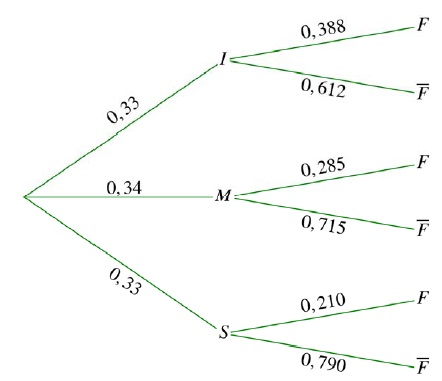
a) Dans quelle tranche de revenus le tabagisme est-il le plus élevé en 2016 ?
0,388 > 0,285 > 0,210.
Le tabagisme est le plus élevé dans la tranche des revenus inférieurs.
b) Pour les tranches de revenus supérieurs et inférieurs, comment le tabagisme a-t-il évolué entre 2000 et 2016 ?
En 2016, pour les revenus inférieurs : 0,388, contre 0,319 en 2000 : le tabagisme croït.
En 2016, pour les revenus supérieurs : 0,210, contre 0,283 en 2000 : le tabagisme décroït.
c) Vérifier que p(F) = 0,294.
Formule des probabilités totales.
p(F) = 0,33 x0,388 +0,34 x0,285 +0,33 x0,210 = 0,12804 +0,0969 +0,0693 ~0,294.
d) En déduire PF(S) et interpréter le résultat dans le contexte de l’exercice.
PF(S) = 0,33 x0,210 / 0,294 ~0,236.
23,6 % des fumeurs appartiennent à la classe supérieure.
|
|
|
|
Exercice 3. ( 7 points )
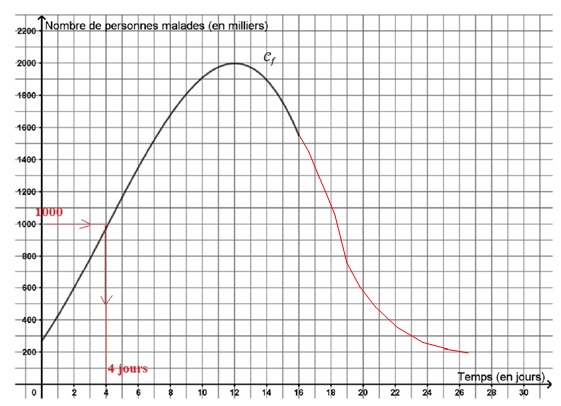
On
modélise l’évolution d’une épidémie dans une région donnée par une
fonction f qui donne le nombre de personnes malades, en milliers, en
fonction du temps compté en jours depuis le début de l’étude.
La fonction f est représentée par la courbe Cf pour les 16 premiers jours de la modélisation.
Partie A : Lecture graphique.
Les réponses aux questions de cette partie ne nécessitent pas de justification.
1) Déterminer une valeur approchée du nombre de personnes malades au début de l’étude.
270 000.
2) Déterminer le nombre de jours au bout desquels le nombre de personnes malades est supérieur à 1 000 000.
3) On sait que :
au-delà du 16e jour, le nombre de personnes malades diminue de plus en plus vite jusqu’au 18e jour ;
à partir du 19e jour, le nombre de personnes malades diminue de moins en moins vite pour passer sous la barre des 200 000 au cours du 26e jour.
Compléter la courbe représentative en proposant une courbe qui soit compatible avec ces informations.
Partie B : Étude de la fonction f.
On admet que, sur l’intervalle [0 ; 16], f est définie par : f(x) = -x3 +12x2 +144 x +270.
1) En utilisant l’expression de la fonction , calculer le nombre d’individus malades au 12e jour de l’étude.
f(12) = -123 +12*122 +144*12 +270 = 144 *12 +270 = 1998 ( 1 998 000 personnes ).
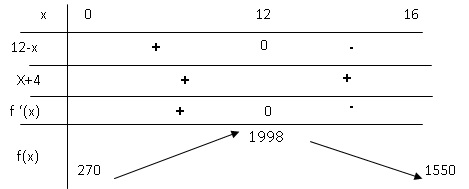
2) On admet que f '(x) = 3(12-x)(x+4).
a) Étudier le signe def '(x) sur l’intervalle [0 ; 16].
b) Construire le tableau des variations de f sur [0 ; 16].
On précisera dans le tableau f(0), f(16) ainsi que la valeur de l’extremum.
3) D’après ce modèle, le nombre de personnes contaminées atteindra-t-il les deux millions ?
Le maximum étant inférieur à 2000, le nombre de malades n'atteindra pas les 2 millions.
|
|
|