Mathématiques, Brevet Asie 2019

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

Exercice 1 . ( 14 points )
Nina et Claire ont chacune un programme de calcul.
Programme de Nina :
Choisir un nombre de départ
Soustraire 1.
Multiplier ce nombre par −2.
Ajouter 2.
Programme de Claire :
Choisir un nombre de départ.
Multiplier le résultat par −0,5.
Ajouter 1 au résultat.
1. Montrer que si les deux filles choisissent 1 comme nombre de départ, Nina obtiendra un résultat final 4 fois plus grand que celui de Claire.
Nina : 1-1 = 0 ; 0 x(-2) = 0 ; 0 +2 = 2 ; Claire : 1 x(-0,5) = -0,5 ; -0,5 +1 = 0,5.
2. Quel nombre de départ Nina doit-elle choisir pour obtenir 0 à la fin ?
(X-1) (-2) +2 = 0 ; -2 X +2+2 = 0 ; X = 2.
3. Nina dit à Claire : « Si on choisit le même nombre de départ, mon résultat sera toujours quatre fois plus grand que le tien ».
A-t-elle raison ?
Nina : (X-1) (-2) +2 = -2X +4 =4(-0,5X+1) ; Claire : X(-0,5) +1= -0,5X+1.
Nina a raison.

Exercice 2 ( 11 points).
Le tableau ci-dessous présente les émissions de gaz à effet de serre pour la France et l’Union Européenne, en millions de tonnes équivalent CO₂, en 1990 et 2013.

	1990	2013
France	549,4	490,2
Union européenne	5680,9	.....

1. Entre 1990 et 2013, les émissions de gaz à effet de serre dans l’Union Européenne ont diminué de 21%.
Quelle est la quantité de gaz à effet de serre émise en 2013 par l’Union Européenne ? Donner une réponse à 0,1 million de tonnes équivalent CO₂ près.
5680,9 x(1-0,21) =4487,9 millions de tonnes.
2. La France s’est engagée d’ici 2030 à diminuer de 2 /5 ses émissions de gaz à effet de serre par rapport à 1990.
Justifier que cela correspond pour la France à diminuer d’environ 1 /3 ses émissions de gaz à effet de serre par rapport à 2013.
Emissions françaises en 2030 : 549,4 x3 / 5 = 329,6 millions de tonnes.
490,2 -329,6 = 160,6.
160,6 / 490,2 ~0,33 soit 1 /3.

Exercice 3 (17 points).
Un programme permet à un robot de se déplacer sur les cases d’un quadrillage. Chaque case atteinte est colorée en gris. Au début d’un programme, toutes les cases sont blanches, le robot se positionne sur une case de départ indiquée par un « d » et la colore aussitôt en gris.
Voici des exemples de programmes et leurs effets :
Le robot avance de 1 case vers l’ouest (1 W).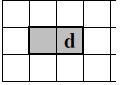

Le robot avance de 2 cases vers l’est, puis de 1 case vers l’ouest, puis de 2 cases vers le nord.( 2E 1W 2N).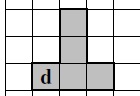

Le robot répète 3 fois le déplacement suivant :
« avancer de 1 case vers le sud puis de 2 cases vers l’est » 3 (1S 2E).

1. Voici un programme : Programme : 1W 2N 2E 4S 2W
On souhaite dessiner le motif obtenu avec ce programme.
Sur votre copie, réaliser ce motif en utilisant des carreaux, comme dans les exemples précédents. On marquera un « d » sur la case de départ.

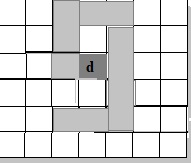
2. Voici deux programmes :
Programme n° 1 : 1S 3(1N 3E 2S)
Programme n° 2 : 3(1S 1N 3E 1S)
a. Lequel des deux programmes permet d’obtenir le motif ci-contre ?

Programme n°2.
b. Expliquer pourquoi l’autre programme ne permet pas d’obtenir le motif ci-dessus.
Le programme n°1 conduit à :

Voici un autre programme :
Programme n° 3 : 4(1S 1E 1N)
Il permet d’obtenir le résultat suivant :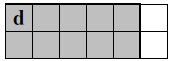

Réécrire ce programme n° 3 en ne modifiant qu’une seule instruction afin d’obtenir ceci :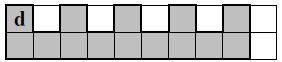

4(1S 2E 1N)

Exercice 4. ( 16 points).
Pour fabriquer un puits dans son jardin, M^me Martin a besoin d’acheter 5 cylindres en béton comme celui décrit ci-dessous.

Caractéristiques d’un cylindre :
• diamètre intérieur : 90 cm
• diamètre extérieur : 101 cm
• hauteur : 50 cm
• masse volumique du béton : 2 400 kg/m³.
Dans sa remorque, elle a la place pour mettre les 5 cylindres mais elle ne peut transporter que 500 kg au maximum.
À l’aide des caractéristiques du cylindre, déterminer le nombre minimum d’allers-retours nécessaires à M^me Martin pour rapporter ses 5 cylindres avec sa remorque.
Volume du cylindre extérieur : 3,14 x1,01² / 4 x0,50 =0,400 m³.
Volume du cylindre intérieur : 3,14 x0,90² / 4 x0,50 =0,318 m³.
Volume du béton : 0,400-0,318 = 0,0819 m³ ; masse : 0,0819 x2400 ~197 kg.
Elle peut transporter deux cylindres soit 3 allers-retours.

Exercice 5. ( 12 points).
La figure ci-contre est codée et réalisée à main levée.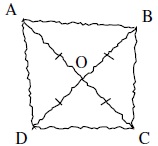

Elle représente un quadrilatère ABCD dont les diagonales se croisent en un point O.
On donne : OA = 3,5 cm et AB = 5 cm.
On s’intéresse à la nature du quadrilatère ABCD qui a été représenté.
1. Peut-on affirmer que ABCD est un rectangle ?
Les diagonales sont égales et se coupent en leurs milieux. Le quadrilatère ABCD est un rectangle.
2. Peut-on affirmer que ABCD est un carré ?
AB² = 5² = 25 ; OA² +OB² = 2 x3,5² = 24,5 différent de AB².
Le triangle AOB n'est pas rectangle en O. Le quadrilatère ABCD n'est pas un carré.

Exercice 6. 14 points.
Voici un tableau concernant les voitures particulières « diesel ou essence » en circulation en France en 2014.

	Nombre de voitures en circulation ( milliers)	Parcours moyen annuel ( km / véhicule)
Diesel	19741	15430
Essence	11984	8644

1. Vérifier qu’il y avait 31 725 000 voitures« diesel ou essence » en circulation en France en 2014.
19741 +11984 =31 725 milliers de voitures.
2. Quelle est la proportion de voitures essence parmi les voitures « diesel ou essence » en circulation en France en 2014 ?
Exprimer cette proportion sous forme de pourcentage. On arrondira le résultat à l’unité.
11984 / 31725 x100 ~38 %.
3. Fin décembre 2014, au cours d’un jeu télévisé, on a tiré au sort une voiture parmi les voitures « diesel ou essence » en circulation en France. On a proposé alors au propriétaire de la voiture tirée au sort de l’échanger contre un véhicule électrique neuf.
Le présentateur a téléphoné à Hugo, l’heureux propriétaire de la voiture tirée au sort.
Voici un extrait du dialogue entre le présentateur et Hugo :
Le présentateur : « Bonjour Hugo, quel âge a votre voiture ? »,
Hugo : « Là, elle a 7 ans ! ».
Le présentateur : « Et combien a-t-elle de kilomètres au compteur ? »,
Hugo : « Un peu plus de 100 000 km. Attendez, j’ai une facture du garage qui date d’hier . . . elle a exactement 103 824 km »,
Le présentateur : « Ah ! Vous avez donc un véhicule diesel je pense ! »
3.a Expliquer pourquoi le présentateur pense que Hugo a un véhicule diesel.
62 % des voitures sont Diesel et celles-ci parcourent en moyenne 15430 km / an ( soit environ 108 000 km en 7 ans).
3.b Expliquer s’il est possible que la voiture de Hugo soit un véhicule essence.
En 7 ans une voiture Essence parcourt en moyenne 8644 x7 = 60500 km. La voiture de Hugo n'est pas un véhicule à essence.

Exercice 7. 16 points.
Les représentations graphiques C₁ et C₂ de deux fonctions sont données dans le repère ci-dessous.
Une de ces deux fonctions est la fonction f définie par f (x) = −2x+8.

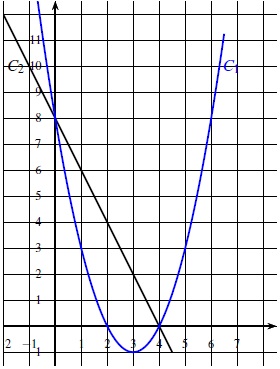
1. Laquelle de ces deux représentations est celle de la fonction f ?
Le graphe de la fonction affine f est une droite passant par les points de coordonnées (0 ; 8) et 4 ; 0) : donc C₂.
2. Que vaut f (3) ?
f(3) = -2 x3 +8 = 2.
3. Calculer le nombre qui a pour image 6 par la fonction f .
6 = -2x +8 ; 2x = 8-6 = 2 ; x = 1.
4. La feuille de calcul ci -dessous permet de calculer des images par la fonction f .

	A	B	C	D	E	F
1	x	-2	-1	0	1	2	3
2	f(x)

Quelle formule peut-on saisir dans la cellule B2 avant de l’étirer vers la droite jusqu’à la cellule G2 ?
= -2*B1+8