Mathématiques,
Brevet Grèce 2019
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
Exercice
1 . ( 12 points ).
Mathilde fait tourner deux roues de loterie A et B comportant chacune quatre secteurs numérotés comme sur le schéma ci-dessous :
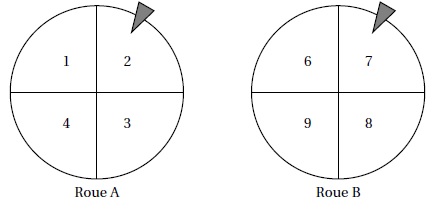
La probabilité d’obtenir chacun des secteurs d’une roue est la même. Les flèches indiquent les deux secteurs obtenus.
L’expérience de Mathilde est la suivante : elle fait tourner les deux
roues pour obtenir un nombre à deux chiffres. Le chiffre obtenu avec la
roue A est le chiffre des dizaines et celui avec la roue B est le
chiffre des unités.
Dans l’exemple ci-dessus, elle obtient le nombre 27 (Roue A : 2 et Roue B : 7).
1. Écrire tous les nombres possibles issus de cette expérience.
16 ; 17 : 18 : 19 ; 26 ; 27 ; 28 ; 29 ;36 ; 37 ; 38 ; 39 ; 46 ; 47 ; 48 ; 49.
2. Prouver que la probabilité d’obtenir un nombre supérieur à 40 est 0,25.
4 cas favorables (46 ; 47 ; 48 ; 49.) sur 16 cas possibles.
4 / 16 = 0,25.
3. Quelle est la probabilité que Mathilde obtienne un nombre divisible par 3 ?
5 cas favorables (18 ; 27 ; 36 ; 39, 48 ) sur 16 cas possibles.
5 / 16 = 0,3125.
Exercice
2 ( 20 points).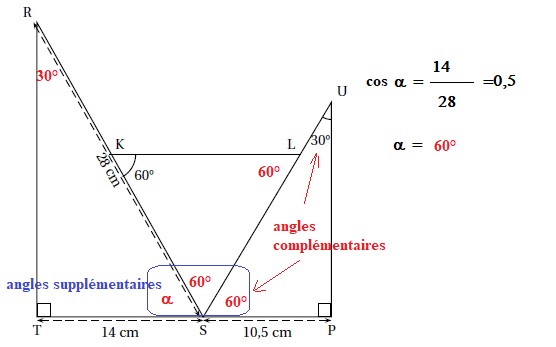
Les points T, S et P sont alignés ; les points R, K et S sont alignés ; les points S, L et U sont alignés.
1. Montrer que la mesure de l’angle TSR est 60°.
Voir ci-dessus
2. Démontrer que les triangles SRT et SUP sont semblables
.Ces deux triangles rectangles ont des angles aigus de même mesure.
3. Déterminer le coefficient de réduction liant les triangles SRT et SUP.
10,5 /14 = 0,75.
4. Calculer la longueur SU.
SU = 0,75 SR = 0,75 x 28 = 21 cm.
5. Quelle est la nature du triangle SKL? A justifier.
Ce triangle est équilatéral : ils possède trois angles égaux à 60°.
Exercice 3 (15
points).
Marc et Jim, deux amateurs de course à pied, s’entrainent sur une piste d’athlétisme dont la longueur du tour mesure 400 m.
Marc fait un temps moyen de 2 minutes par tour.
Marc commence son entrainement par un échauffement d’une longueur d’un kilomètre.
1. Combien de temps durera l’échauffement de Marc ?
1 km = 2,5 tours ; durée 2 x2,5 = 5 minutes.
2. Quelle est la vitesse moyenne de course de Marc en km/h ?
0,4 km parccouru en 1 / 30 heure soit 0,4 x30 = 12 km / h.
À la fin de l’échauffement, Marc et Jim décident de commencer leur
course au même point de départ A et vont effectuer un certain nombre de
tours.
Jim a un temps moyen de 1 minute et 40 secondes par tour.
Le schéma ci-dessous représente la piste d’athlétisme de Marc et Jim
constituée de deux segments [AB] et [CD] et de deux demi-cercles de
diamètre [AD] et [BC).
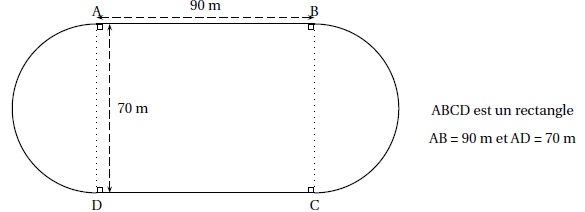
3. Calculer le temps qu’il faudra pour qu’ils se retrouvent ensemble, au même moment, et pour la première fois au point A.
Puis déterminer combien de tours de piste cela représentera pour chacun d’entre eux.
Jim a fait un tout de piste de plus que Marc.
Marc fait n tours en 120 n secondes.
Jim fait n+1 tours en 100(n+1) secondes.
120n = 100(n+1) ; 20 n = 100 ; n = 5.
Au bout de 10 minutes, Marc a fait 5 tours et Jim a réalisé 6 tours.
|
|
|
Exercice
4. ( 16 points).
Pour
occuper son petit frère, Lucie, qui aime bien l’informatique, décide de
fabriquer des rosaces à colorier. Elle décide de partir d’un motif
ayant la forme d’un losange. A l’aide d’un logiciel de programmation
assisté (type scratch), elle a représenté le motif suivant.
Il s’agit d’un losange dont les côtés ont pour longueur 50 pixels et dont les angles aigus mesurent 30°et les angles obtus 150°.
Afin de représenter ce losange, elle a écrit le programme suivant :
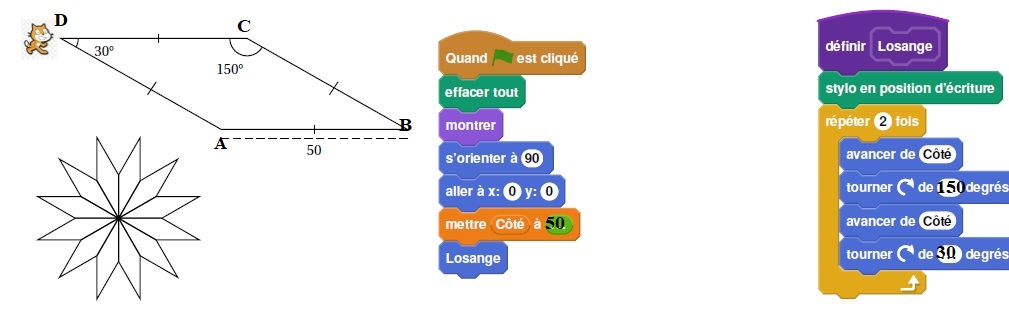
1.
Compléter le programme ci-dessus en remplaçant les pointillés par les
bonnes valeurs pour que le losange soit dessiné tel qu’il est défini.
Mettre côté à 50 :
tourner de 150° :
avancer de côté :
tourner de 30°.
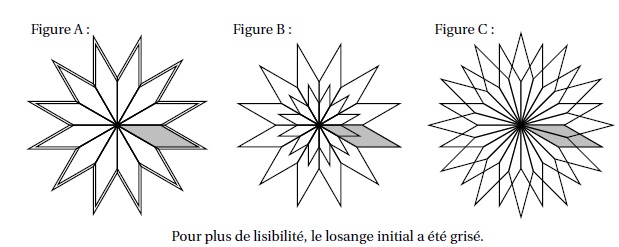
2. En utilisant le losange ci-dessus, elle obtient la rosace qui n’est pas en vraie grandeur :
Quelle
transformation géométrique, partant du premier losange ABCD et répétée
12 fois, a été utilisée pour obtenir cette figure? Définir le mieux que
vous pouvez cette transformation.
Rotation de centre D et d'angle 30°.
3.
Pour finir, Lucie souhaite encore compléter cette rosace de trois
façons différentes. Pour cela trois programmes ont été effectués.
Recopier sur votre copie le numéro des trois programmes, et pour chacun, la lettre de la figure qui lui est associée.
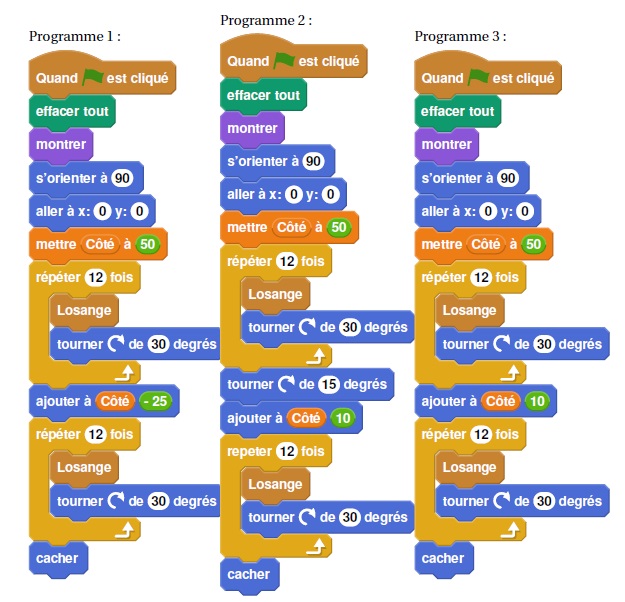
Programme 1 ; figure B : programme 2 : figure C ; programme 3 : figure A.
Exercice
5. ( 15 points).
On donne le programme de calcul suivant :
Choisir un nombre
Ajouter 1
élever le résultat au carré
soustraire au résultat le carré du nombre de départ.
1. Montrer que lorsqu’on choisit le nombre 2 au départ, on obtient le nombre 5 au final.
2+1 = 3 ; 32 = 9 ; 9-22 =5.
2. Quel résultat obtient-on lorsqu’on choisit au départ le nombre −3?
-3+1 = -2 ; (-2)2 = 4 ; 4-(-3)2 = -5.
3. On
définit une fonction f qui, à tout nombre x choisi à l’entrée du
programme, associe le résultat obtenu à la fin de ce programme.
Ainsi, pour tout x,on obtient f (x) = (x +1)2 −x2.
Montrer que f (x) = 2x +1.
On développe : x2 +2x+1-x2 = 2x+1.
4. Cette question est un questionnaire à choix multiples (QCM).
Dans chaque cas, une seule réponse est correcte. Pour chacune des
questions, écrire sur la copie le numéro de la question et la bonne
réponse.
Aucune justification n’est demandée.
La représentation graphique de la fonction f est : A ; B ; C.
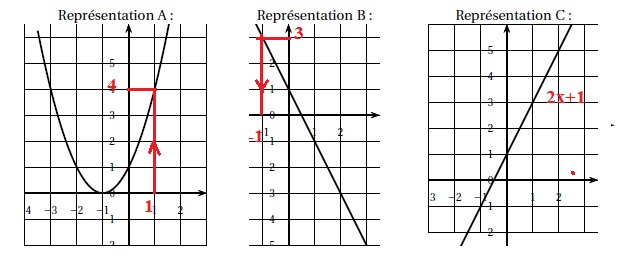
En utilisant la représentation A, l'image de 1 par la fonction représentée est : 4 ; -2 ; 0.
En utilisant la représentation B, l’antécédent de 3 par la fonction représentée est : -1 ; -5 ; 2.
|
|
Exercice 6. 22 points.
Dans le village de Jean, une brocante est organisée chaque année lors du premier week-end de juillet.
Jean s’est engagé à s’occuper du stand de vente de frites. Pour cela,
il fabrique des cônes en papier qui lui serviront de barquette pour les
vendre.
Dans le fond de chaque cône, Jean versera de la sauce : soit de la mayonnaise, soit de la sauce tomate.
Il décide de fabriquer 400 cônes en papier et il doit estimer le nombre
de bouteilles de mayonnaise et de sauce tomate à acheter pour ne pas en
manquer.
Voici les informations dont Jean dispose pour faire ses calculs :
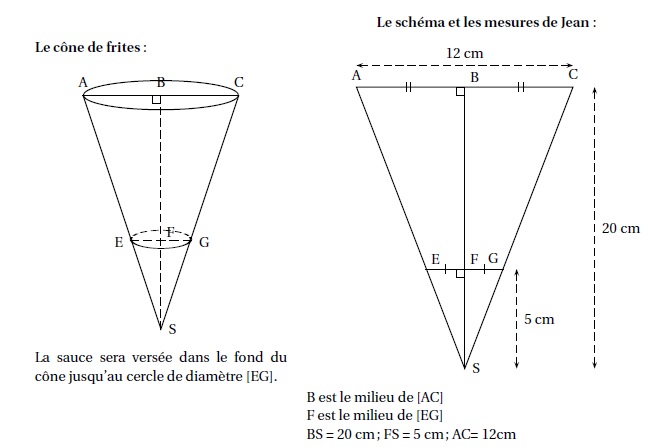
Les acheteurs :
80% des acheteurs prennent de la sauce tomate et tous les autres prennent de la mayonnaise.
La bouteille de mayonnaise est assimilée à un cylindre de révolution dont le diamètre de base est 5 cm et la hauteur est 15 cm.
La bouteille de sauce tomate a une capacité de 500 mL.
1. Montrer que le rayon [EF] du cône de sauce a pour mesure 1,5 cm.
(AC) et (EF) sont parallèles.
A, E et S sont alignés ; B, F et S pont alignés.
Thalès : EF / AB = FS / BS ; EF =AB x FS / BS = 6 x5 /20 =1,5 cm.
2. Montrer que le volume de sauce pour un cône de frites est d’environ 11,78 cm3.
V = p EF2 xFS / 3 = 3,14 x1,52 x5 / 3 =11,78 cm3.
3. Déterminer le nombre de bouteilles de chaque sauce que Jean devra acheter.
Tomate : 400 x0,8 = 320 ; 320 x11,78 ~3770 cm3 soit 3770 / 500 =7,5 ( 8 bouteilles de sauce tomate).
Mayonnaise : 80 ; 80 x11,78 = 942,4 cm3.
Volume d'une bouteille de mayonnaise : p r2 h =3,14 x2,52 x15 ~295 cm3 .
942,4 / 295 ~3,2 ( 4 bouteilles de sauce mayonnaise ).
|
|