La
physique dans la cuisine, de l'huile dans l'eau, la cuisson des pâtes,
Capes physique chimie 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
Ce
problème propose d’aborder quelques-unes des nombreuses notions de
physique sur lesquelles on peut s’interroger en cuisinant.
Partie 1 – De l’huile dans
l’eau.
Dans cette partie, on s’intéresse à quelques effets de l’huile versée
sur de l’eau. On analysera un sujet de baccalauréat blanc.
Analyse du sujet de baccalauréat blanc
Le sujet est posé au cours d’un baccalauréat blanc proposé à 4 classes
de terminale scientifique ; 148 élèves ont composé.
Un enfant tient dans sa main une bouteille d’huile et observe les
gouttes d’huile tomber dans une casserole d’eau destinée à la cuisson
des pâtes.
L’huile et l’eau sont deux liquides non miscibles. Lorsqu’on les verse
l’un sur l’autre, et de n’importe quelle manière, on constate
inexorablement que l’huile surnage sur l’eau.
Données :
- Masse volumique de l’huile : ρH = 800 kg.m–3 ;
- Masse volumique de l’eau : ρE = 1,00.103 kg.m–3
;
- Intensité de pesanteur : g = 10 m.s–2 ;
- Masse volumique de l’air : ρ = 1,30 kg.m–3.
Lorsque la goutte est dans l’air, on suppose que les frottements sont
négligeables.
Q1. Répondre au QCM
proposé aux élèves, en complétant le tableau suivant.
1.1. Avant que la
goutte d’huile ne se détache, elle est soumise à l’action mécanique :
a) de la Terre b) de l’enfant ; c) de l’huile d) de la bouteille
1.2. La goutte
d’huile qui s’est détachée est soumise à l’action mécanique :
a) de la Terre b) de l’enfant ; c) liée à la vitesse initiale d) de la
bouteille
L’enfant, amusé, remplit une bassine d’eau et projette une goutte
d’huile, avec une vitesse initiale v0, verticale
descendante, pour reproduire ce phénomène.
1.3. Quelle est la
nature du mouvement de la goutte ?
a) Parabolique b) Rectiligne uniforme ; c) Rectiligne uniformément
accéléré d) Rectiligne uniformément ralenti
L’enfant reproduit le phénomène avec une goutte d’eau et une goutte
d’huile qu’il laisse à présent se détacher seules (sans vitesse
initiale).
1.4. Une goutte
d’eau de même volume que la goutte d’huile possède :
a) la même masse b) une masse plus grande
c) une masse plus petite d) on ne peut pas savoir
1.5. La goutte
d’eau de même volume chutera :
a) plus vite que la goutte d’huile b) moins vite que la goutte d’huile
c) à la même vitesse que la goutte d’huile d) on ne peut pas savoir.
|
a
|
b
|
c
|
d
|
1.1
|
109
|
30
|
56
|
89X
|
1.2
|
143
|
4
|
69
|
2
|
1.3
|
2
|
16
|
134
|
2
|
1.4
|
0
|
124
|
22
|
1
|
1.5
|
61
|
15
|
72
|
2
|
Le tableau ci-dessous regroupe le nombre de cases cochées par les
élèves sur le QCM.
.
|
a
|
b
|
c
|
d
|
1.1
|
X
|
|
|
X
|
1.2
|
X
|
|
|
|
1.3
|
|
|
X
|
|
1.4
|
|
X
|
|
|
1.5
|
|
|
X
|
|
Quelle
ambiguïté, qui pourrait être à l’origine des erreurs observées,
présente la question 1.1.? Proposer une reformulation.
La gouute d'huile ne se détache pas de la bouteille mais du filet
d'huile.
Reformulation : "Avant que la goutte d’huile ne se détache
du filet d'huile, elle est soumise à l’action mécanique :"
Quelles confusions les
questions 1.2. et 1.5. permettent de mettre en évidence chez les élèves
? Proposer dans chaque cas, une courte activité de remédiation
(éventuellement à caractère expérimental) en 5 lignes maximum
permettant de limiter ces confusions.
Confusion entre vitesse et force.
Activités proposées :
Construire un diagramme interaction-goutte d'huile ( Q1.2).
Chute d'une plume puis d'une bille en acier dans un tube de Newton ( en
réalisant le vide ). Chronométer la durée des chutes.
Q2. Rédiger une
correction des parties 2 (chute dans l’air) et 3 (des ondes à la
surface de l’eau) du sujet fourni.
2. Chute dans l’air.
À la date t = 0 s, l’enfant lâche une goutte d’huile de volume V =
0,050 mL, d’une hauteur H = 1,0 m au-dessus d’une bassine contenant de
l’eau.
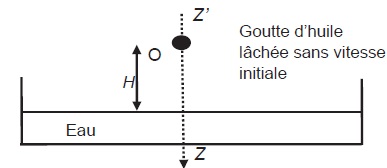
2.1. Sur l’axe Z’Z,
on fait coïncider l’origine O avec la position de la goutte juste au
moment du lâcher. En appliquant la deuxième loi de Newton, déterminer
la valeur de l’accélération de la goutte et établir l’équation horaire
de son mouvement.
La goutte n'est soumise qu'à son poids. La seconde loi de Newton
conduit à : a = g = 10 m s-2.
La vitesse est une primitive de l'accélération et la vitesse initiale
est nulle.
v = gt.
La position est une primitive de la vitesse et la position initiale est
l'origine de l'axe.
z = ½gt2.
2.2. Avec quelle
vitesse la goutte d’huile frappe-t-elle la surface de l’eau ?
H = ½gt2 ; t =(2H /g)½ ; repport dans
l'expression de la vitesse : v = g(2H /g)½
=(2gH)½.
Q3. Directement sur la copie de
l’élève donnée corriger et annoter les parties 2 et 3, en identifiant
les erreurs commises. Rédiger ensuite un commentaire général sur votre
copie.


|
...
|
|
|
....
|
3. Des ondes à la surface de l’eau.
Lorsque la goutte d’huile arrive dans l’eau, elle crée une déformation
de la surface avant de s’étaler. Avec une caméra, l’enfant filme les
ondes à la surface de l’eau. La caméra a enregistré le film à 10 images
par seconde. On reproduit ci-dessous l’image n°1 réalisée à l’instant t0
= 0 s correspondant au contact de la goutte d’huile avec l’eau.
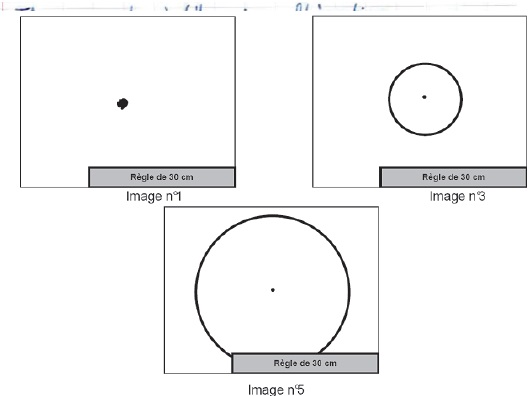
Les troisième et cinquième images du film (image n°3 et image n°5) sont
également, représentées ci-dessous.
Figure 3 - document en vue de dessus ; le cercle noir représente le
front d’onde.
3.1. Qu’appelle-t-on « onde » ?
Une onde est la propagation d'une perturbation sans transport de
matière, mais avec transport d'énergie.
3.2. Les ondes qui
apparaissent sur la surface de l’eau sont-elles transversales ou
longitudinales ? Justifier.

3.3. À l’aide des
données expérimentales, calculer la vitesse de propagation des ondes à
la surface de l’eau.

Le cours est connu.
Des difficultés pour lire correctement le texte ( conditions initiales
de chute).
Un résultat incohérent est reconnu.
|
Partie 2
– La cuisson des pâtes.
A priori, c’est simple, il n’y a qu’à suivre la recette !
Conseil de préparation :
Verser les pâtes dans l’eau bouillante salée (1 L d’eau pour 100 g de
pâtes). Remuer et laisser cuire à découvert 7 à 8 minutes. Egoutter sans
rincer. Servir rapidement.
Ingrédients :
Semoule de blé dur de qualité supérieure, oeufs frais 30% (soit 320 g par kilo de semoule).
Des consommateurs se posent quand même certaines questions :
Lu sur un forum : « Peut-on faire cuire des pâtes à la cocotte-minute ? »
Réponse 1 : « Il ne faut surtout pas mettre des pâtes à la cocotte
(essayez de couvrir une casserole contenant des pâtes,
ça déborde). Dans la cocotte, c'est pareil. »
Réponse 2 :« Non, tout simplement non ! Ça n'est tout de même pas compliqué, ni long, de faire cuire des pâtes ! »
Réponse 3 :« Bien sûr que si, mais pas pour qu’elles soient tendres.
En altitude (chez moi), l’eau bout à 91°, ce qui fait des pâtes
pâteuses et collantes, et ce n’est pas bon. La solution est de les cuire à la cocotte en faisant
tourner la soupape au
minimum, ça doit faire dans les 102°. »
À l’aide des questions numérotées de Q4 à Q9 ci-dessous, on cherche à résoudre le problème suivant :
« À quelle altitude réside cet internaute et quelle est la valeur de la
température d’ébullition de l’eau dans son autocuiseur (cocotte-minute) ? »
Données :
- Constante des gaz parfaits : R = 8,314 SI ;
- Masse volumique du mercure : ρHg = 13,6.103 kg.m–3.
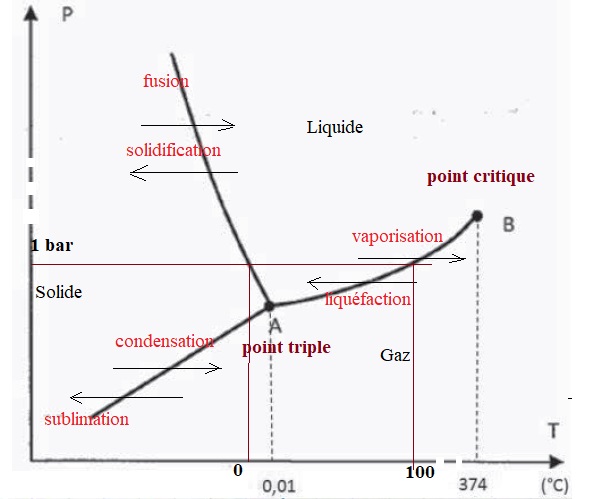
Diagramme (P, T) de l’eau.
Q4. On donne
l’allure du diagramme (P, T) de l’eau. Après l’avoir reproduite sur
votre copie, nommer les points A et B, placer les états de la matière
dans les différentes
zones du diagramme (P, T) de l’eau et nommer les changements d’états correspondants aux différentes branches du diagramme.
Représenter l’isobare P = 1 bar et indiquer la valeur des températures caractéristiques sur cette courbe.
Tracé expérimental de la courbe de pression de vapeur saturante de l’eau
Q5. Expliquer
successivement l’intérêt d’avoir deux ballons, puis celui de les relier
par un tube calorifugé et pour finir, l’intérêt de purger le montage de
l’air qu’il contient.
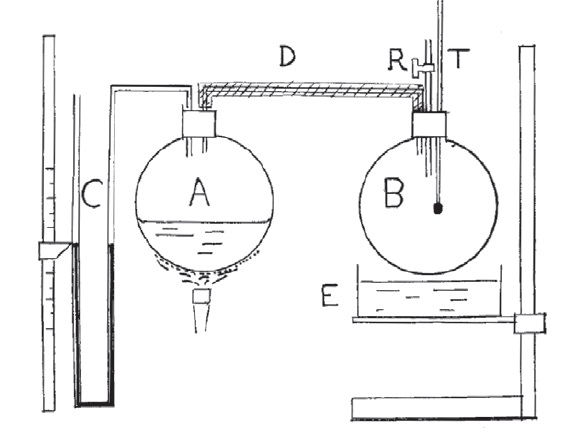
Deux ballons A et B (1 L environ) sont reliés par un tube D, calorifugé.
- Ballon A : de l'eau et un manomètre C à mercure et air libre dont les branches ont environ 80 cm de hauteur.
- Ballon B : un robinet R et un thermomètre T à petit réservoir placé au centre du ballon.
E est un récipient d'eau froide monté sur support à crémaillère
- Veiller à l'étanchéité des joints.
2.- Manipulation.
- Porter A à ébullition jusqu'à ce que T indique la température
d'ébullition de l'eau et que l'appareil soit purgé d'air (R ouvert).
- Puis fermer R, arrêter le chauffage et laisser l’ensemble refroidir.
- On note simultanément la température lue sur T et la pression de la vapeur d'eau déduite de l'observation de C.
- On pourra activer le refroidissement de B avec le récipient E (en fin d'expérience vers 40°C et avec précaution).
3. - Résultats.
En 20 minutes on relève la courbe de pression de vapeur saturante entre
100°C et 40°C avec des écarts extrêmement faibles par rapport aux
données des formulaires, écarts
toujours compatibles avec les incertitudes de mesure.
Cette expérience est facile à reprendre à tout moment - si un point
semble s'écarter anormalement de la valeur théorique : on chauffe à
nouveau.
Chauffage et refrodissement rapide et simple à mettre en oeuvre.
Themomètre situé loin de la flamme. Expérience réalisée à volume constant ( volume du second ballon ).
Les pressions et la température sont identiques dans les deux ballons du fait du tube D calorifugé.
L'air étant purgé, le système est diphasique ( vapeur et liquide).
Q6. Expliquer brièvement, les principes physiques mis en oeuvre dans le montage pour mesurer la température et la pression.
À quelle différence de hauteur de mercure la mesure de pression 0,40 bar correspond-elle ?
Représenter le manomètre C lors de cette mesure.
Pour quelle(s) raison(s) n’utilise-t-on plus ce dispositif de nos jours ?
Dans le manomètre : Pinitiale = Patmosphérique. ( robinet ouvert)
Robinet fermé
: la pression diminue dans le ballon A ; le mercure monte dans la
branche droite du manomètre et descend dans sa branche gauche.
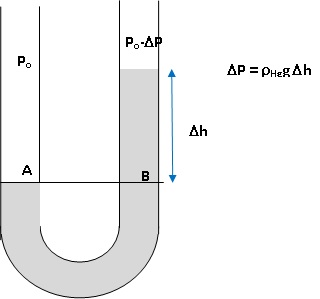
PA = P0 ; PB = P0 -rHg g Dh ; PA = PB. (principe fondamental de l'hydrostatique)
(P0 -0,40) 105=rHg g Dh ;
Dh = 0,60 x105 /(13600 x9,81) =0,45 m.
Inconvénient : le mercure utilisé est très toxique.
Q7. Réalisation plus récente de l’expérience.

On souhaite interfacer et automatiser les mesures de température et de
pression à l’aide d'un système d’acquisition . Choisir, en justifiant,
les capteurs à utiliser, puis
décrire le protocole d’acquisition adapté aux mesures. Préciser son paramétrage.
Donner les résultats de mesure de température et de pression
correspondant à 0,40 bar ; les écrire correctement, avec leur
incertitude.
Capteur de température : sonde Pt100 ; capteur de pression absolue.
Acquisition en mode XY, pas de 1°C. On sélectionne la température comme référence.
Incertitudes dues aux instruments : U(P) = 0,5 /100 x0,40 = 2 10-3 bar ; U(T) = 0,1°C.
Incertitude de lectures du graphique : U(Plecture) =0,02 bar et U(Tlecture) = 1°C.
P=0,40 ±0,02 bar ; T = 75 ±1 °C.
Détermination de l’altitude à laquelle réside l’internaute.
Q8. À partir de la
courbe suivante, déterminer la valeur de la pression pour que la
température d’ébullition de l’eau soit de 91°C, valeur donnée par
l’internaute.
Démontrer que si on suppose que l’atmosphère, assimilée à un gaz
parfait, est en équilibre isotherme à la température T, alors la
pression P(z) à l’altitude z est donnée par :
P(z) = P0 exp[Mgz /(RT)]
Identifier les paramètres P0 et M introduits dans cette expression, préciser leurs valeurs et leurs unités. Préciser les unités de R et T.
En déduire l’altitude à laquelle réside l’internaute.
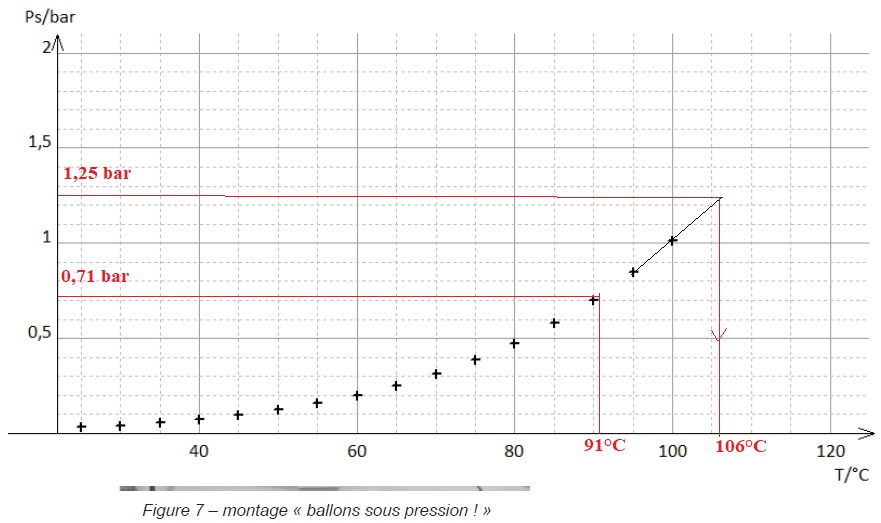
A l'ébullition la pression de vapeur saturante est égale à la pression ambiante ~0,71 bar.
Loi des gaz parfaits P V= n RT soit P = nRT / V.
Principe de l'hydrostatique : P = P0 -r g z soit dP = - r g dz.
dP / P = - r g V / (nRT) dz.
n = m / M et r = m / V ; r V =nM.
dP / P = - g M / (RT) dz.
Intégrer : ln(P / P0) =-Mg /(RT) z.
P = P0 exp[-Mg /(RT) z].
M(air) = 28,8 g / mol ; R =8,314 J mol-1 K-1. P0 = 1,013 105 Pa pour z = 0. T température en kelvin.
z = -RTln(P / P0) /(Mg) =-8,314 x(273+91) ln(710 /1013) /(0,0288 x9,81) ~3,8 103 m.
Détermination de la température d’ébullition de l’eau à l’intérieur de l’autocuiseur de l’internaute.
Q9. Résolution de
problème : quelles sont les valeurs de la pression et de la température
à l’intérieur de l’autocuiseur à l’altitude à laquelle réside
l’internaute ?
Au niveau de la mer ( z =0), la soupape s'ouvre lorsque la pression à l'intérieur de l'auto-cuiseur atteint 1,56 bar.
Surpression : 1,56 -1,013 ~0,55 bar.
A 3,8 km d'altitude, la pression à l'intérieur vaut : 0,71 +0,55 = 1,26 bar.
Température d'ébullition dans l'auto-cuiseur : 106°C ( lecture graphe).
|
|
|











