Mathématiques, concours interne TSPEI 2018

Mathématiques, Concours interne TSPEI 2018.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.

Premier problème.
Soit la fonction f définie sur [-p ; +p ] par f(x) = 1 +cos (x).
1. Calculer f(0), f(p/2) et f(p).
f(0)=1 + cos (0) = 1 +1 = 2.
f(p/2) = 1 +0 = 1 ; f(p)=1-1= 0.
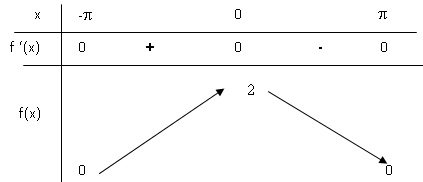
2. Déterminer la dérivée de la fonction f. En déduire le tableau de variations de f.
f '(x) = - sin(x).
f '(x) =0 pour x = ±p et 0.

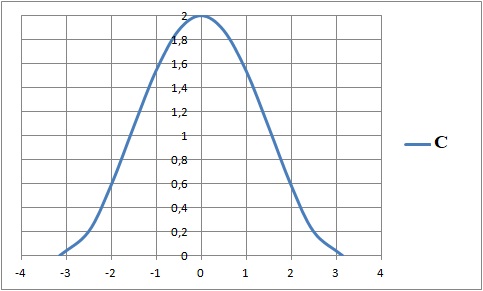
3. Construie la courbe C représentative de f.

Si A et B sont deux réels, on désigne par min{A, B} le plus petit des nombres a et B.
Par exemple min{2, 4}=2.
On définit sur R la fonction g telle que : pour tout réel x, g(x) = min {1, 1 +cos(x) }.
4. Montrer que la fonction g est paire et périodique de période 2p.
Sur ]-p /2 ; + p /2[, 1 +cos(x) > 1 : g(x) = 1.
Sur [-p , -p/2 ] et sur [p/2 , p ], 1 +cos (x) <1 ; g(x) = 1 +cos (x).
Cos(x) est paire, donc 1 + cos(x) est paire.
La période de cos(x) est égale à 2p ; g est périodique de période 2p.
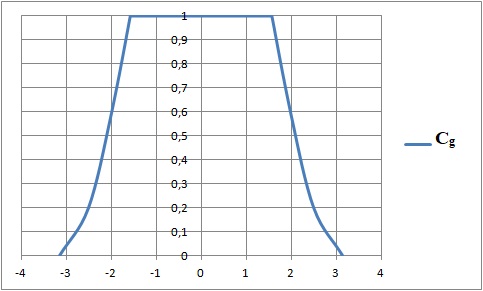
5. Construire C_g la courbe représentative de g sur l'intervalle [-p ; +p ].

5. Calculer les intégrales suivantes :

.....

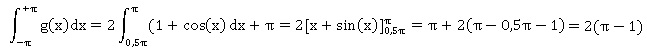
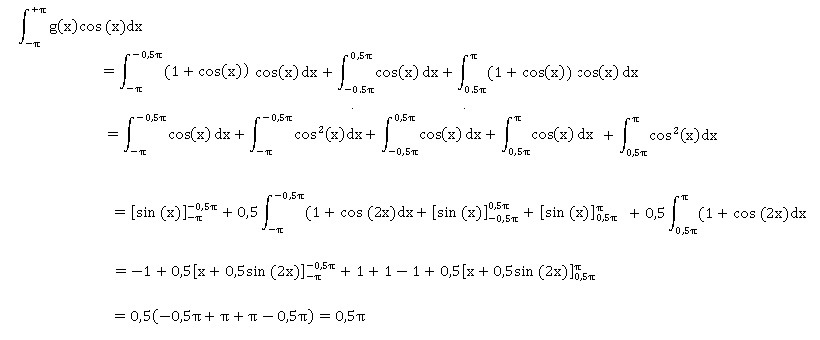
Deuxième problème.

Hommes
Femmes
Ensemble

Population totale
30
33
63

Moins de 20 ans
8
8
16

20 à 64 ans
18
19
37

65 ans ou plus 4
6
10

Ces données ont été arrondies au million d'individus.
Les quantités demandées sans les questions seront arrondies a 10^-2 près.
1. Un individu est sélectionné au sein de la population étudiée.
1.1. Quelle est la probabilité que ce soit un homme ?
30 / 63 = 10 / 21 ~0,476 ~0,48.
1.2. Quelle est la probabilité que l'individu choisi ait au moins 65 ans.
10 / 63 ~0,159 ~0,16.
1.3. Quelle est la probabilité que l'individu choisi soit une femme d'au moins 65 ans ?
Tous les événements sont supposés indépendants.
On précisera l'hypoyhèse permettant d'obtenir ces résultats.
6 / 63 = 0,095.
2. On s'aperçoit que l'individu choisi est une femme. Qu'elle est la probabilité qu'elle ait plus de 65 ans ?

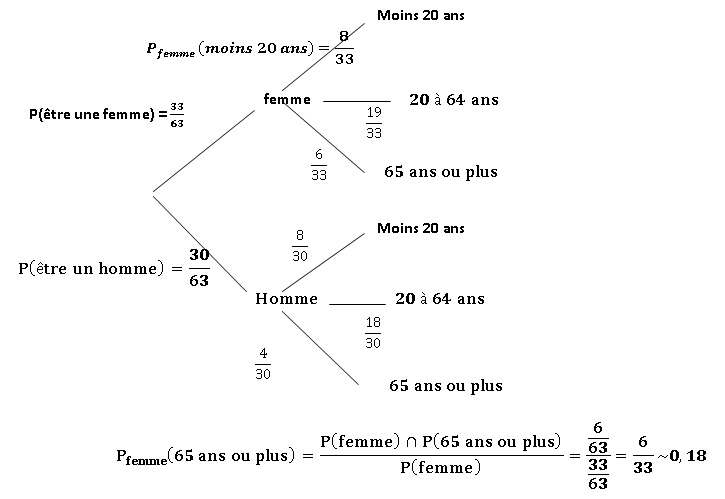
3.
On choisit au hasard 12 individus au sein de la population. Compte tenu de la taille de celle-ci, on supposera que les tirages sont effectués " avec remise". On appelle X la variable aléatoire égale au nombre d'hommes figurant dans l'échantillon de 12 personnes.
3.1. Quelle est la loi de probabilité de X ? On donnera son espérance et sa variance.
Deux issues sont possibles : être un homme ou être une femme à chaque tirage.
Les tirages sont indépendantes les uns des autres.
X suit la loi binomiale de paramètre :
n = 12 et p = 30 / 63 ~0,4762.
Espérance µ =np = 12 x30 / 63 = 5,71 ~5,7
variance V = n p (1-p) =12 x 30 / 63 x 33 / 63 = 2,993~3,0.
écart type s = 2,993^½ =1,73.
3.2. Quelle est la probabilité que l'on ait, parmi les 12 personnes, autant d'hommes que de femmes ?
P(X = 6) =0,2225 ~0,22.

.

menu