Mathématiques,
logarithme, exponentielle, équation différentielle, bac Centres
étrangers 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Fonction logarithme (
5 points).
Partie A.
Dans un pays une maladie touche la population avec une probabilité de
0,05. On possède un test de dépistage de cette maladie.
On
considère un échantillon de n personnes ( n > 20) prises au
hasard dans la population, assimilé à un tirage avec remise.
On teste l'échantillon selon cette méthode : on mélange le sang de ces
n individus, on teste le mélange. Si le test est positif, on effectue
une analyse individuelle de chaque personne.
Soit Xn la variable aléatoire qui donne le nombre d'analyses
effectuées.
1. Montrer que Xn
prend les valeurs 1 et n+1.
Test négatif : on a effectué une seule analyse.
Test positif : on effectue l'analyse du mélange puis les analyses des n
personnes soit n+1 analyses.
2. Prouver que p(Xn
= 1) = 0,95n. Etablir la loi de Xn.
On a effectué l'analyse du mélange et le test est négatif.
Probabilité qu'une personne ne soit pas malade : 0,95.
Probabilité que n personnes ne soit pas
malades : 0,95n.
xi
|
1
|
n+1
|
P(Xn=xi)
|
0,95n
|
1-0,95n
|
3.
Que représente l'espérance dans le cadre de cette expérience ? Montrer
que E(Xn) = n+1-n x0,95n.
L'erspérance donne le nombre moyen d'analyses.
E(Xn)
=0,95n +(n+1)(1-0,95n)=0,95n +n
+1 -(n+1)0,95n =n+1-n x0,95n.
Partie B.
1. On considère la
fonction f définie sur [20 ; +oo[ par f(x) = ln(x) + x ln(0,95).
Montrer que f est décroissante.
f '(x) = 1/x +ln(0,95) = (1+xln(0,95) / x.
x > 20 ; x ln(0,95) < -1,026 ; (1+xln(0,95)
<0.
f '(x) étant négatif, f(x) est
décroissante.
2. Montrer que la
limite de f(x) en plus l'infini est moins l'infini.
f(x) = x ( ln(0,95) +ln(x) / x).
Or ln(x) / x) tend vers zéro si x tend
vers plus l'infini.
ln(0,95) < 0 ; f(x) tend vers moins l'infini si x tend vers plus
l'infini.
3. Montrer que f(x) =0 admet une
seule solution a
sur [20 ; +oo[. Donner un encadrement à 0,1 de cette solution.
f(x) est strictement décroissante.
f(20) ~1,97 ; f(x) tend vers moins l'infini quand x tend vers plus
l'infini.
D'après le théorème de la bijection, f(x) =0 admet
une seule solution a
sur [20 ; +oo[.
La calculatrice donne a
= 87,0.
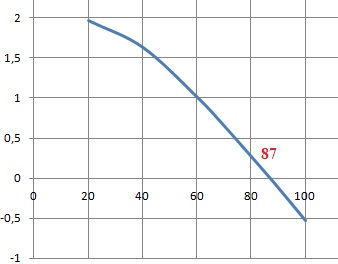
Si n > 87, f(x) < 0 ; si x < 87, f(x) > 0.
Partie C.
On
cherche à comparer deux types de dépistages. La première méthode est
décrite dans la partie A. La seconde consiste à tester tous les
individus. La première méthode permet de diminuer le nombre d'analyses
dès que E(Xn) < n.
En utilisant la
partie B, montrer que la première méthode diminue le nombre d'analyses
pour des échantillons comportant 87 personnes au maximum.
E(Xn)
= n+1-n x0,95n < n.
1-n
x0,95n < 0 ; 1 < n x0,95n .
ln(1) < ln(n) +n ln(0,95).
0 <
ln(n) +n ln(0,95).
Or f(x)
= ln(x) + x ln(0,95) est positif si x < 87.
Equation différentielle.
Partie A.
Soit g la fonction définie par : g(x) =2e-x/3+2x/3-2.
1. Montrer que g'(x) = -2/3 e-x/3 +2/3.
g'(x) = 2(-1/3) e-x/3+2/3 = -2/3 e-x/3 +2/3 = 2 /3(1-e-x/3 ).
2. En déduire le sens de variation de la fonction g sur R.
g'(x) = 0 si e-x/3 = 1 soit x=0.
g'(x) > 0 si x >0 et g(x) est croissante.
g'(x) < 0 si x < 0 et g(x) est décroissante.
3. Déterminer le signe de g(x).
Si x tend vers moins l'infini, g(x) tend vers plus l'infini.
g(0) =0 ( minimum ).
Si tend vers plus l'infini, g(x) tend vers plus l'infini.
g(x) décroit de plus l'infini à zéro puis croît ensuite ; g(x) est donc positive ou nulle sur R.
Partie B.
1. On considère l'équation différentielle (E) : 3y'+y = 0. Résoudre (E).
y'+y/3=0.
y = A e-x/3 avec A une constante.
2. Déterminer la solution particulière dont la courbe représentative passe par le point M(0 ; 2).
2 = A e0 soit A = 2.
3. Soit la fonction définie par f(x) = 2e-x/3 et Cf sa courbe représentative.
a. Montrer que la tangente T à la courbe Cf au point M admet une équation de la forme y = -2x / 3 +2.
Coefficient directeur de la tangente T : g'(x) =-2/3e-x/3 ; g(0) = -2/3.
T passe par M(0 ; 2) : 2 = -2 / 3 *0 +b ; b = 2.
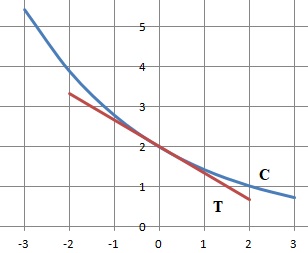
b. Etudier sur R la position de cette courbe par rapport à sa tangente.
2e-x/3 -(-2x/3+2) = 2e-x/3 +2x/3-2 = g(x).
Or g(x) > 0, donc la courbe Cf est au dessus de la tangente T.
Partie C.
1. Soit A le point de la courbe Cf d'abscisse a, a réel quelconque.
Montrer que la tangente à la courbe Cf au point a coupe l'axe des abscisses en un point P d'abscisse a+3.
Coefficient directeur de cette tangente : f '(a) =-2/3e-a/3 ;
Le point A ( a ; f(a) =2e-a/3 ) appartient à la tangente.
Equation de la tangente : y = -2/3e-a/3 x+b.
2e-a/3 = -2a/3e-a/3 +b.
b = 2e-a/3+2a/3e-a/3 =2e-a/3 (1+a/3).
y = -2/3e-a/3 x+2e-a/3 (1+a/3).
Intersection avec l'axe des abscisses : y = 0.
2/3e-a/3 x=2e-a/3 (1+a/3).
x=3(1+a/3 )= a+3.
2. Expliquer la construction de la tangente à la courbe C au point B d'abscisse -2.
x = a = -2 ; f(-2) = 2e2/3 ;
La tangente coupe l'axe des abscisses en x = a+3 =-2+3 = 1.
|
...
|
....
|
Fonction exponentielle. (5 points)
Partie A.
Résolution d'une équation différentielle.
Soit la fonction f(x) = ex+ax+be-x définie sur R
avec a et b réels.
On donne la représentation graphique de la courbe C représentant la
fonction f et la tangente à la courbe au point d'abscisse zéro.
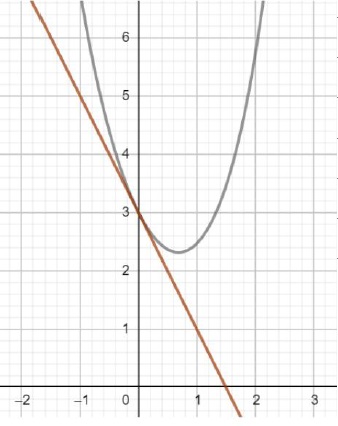
1. Donner les
valeurs de f(0) et de f '(0) par lecture graphique.
f(0) = 3 ; f '(0) = -3 / 1,5 = -2 ( pente de la tangente).
2. Exprimer f(0) en fonction de b et
en déduire la valeur de b.
f(0) =e0+be-0 = 1+b = 3 ; b = 2.
3.a Donner l'expression de f
'(x).
f '(x) =ex+a -2e-x
.
b. Déterminer a puis l'expression
de f.
f '(0) =e0+a -2e-0
=a-1 = -2 ; a = -1.
f(x) = ex-x+2e-x .
4. On considère l'équation
différentielle y'+y = 2ex-x-1. (E).
a. Vérifier que la
fonction g(x) =ex-x+2e-x est solution de (E).
g'(x) = ex-1-2e-x.
Repport dans (E) : ex-1-2e-x+ex-x+2e-x
=2ex-x-1 est bien vérifié.
b. Résoudre l'équation
différentielle y' +y =0.
y = A e-x avec A une constante.
c. En déduire toutes les solutions
de (E).
y = A e-x +ex-x+2e-x
.
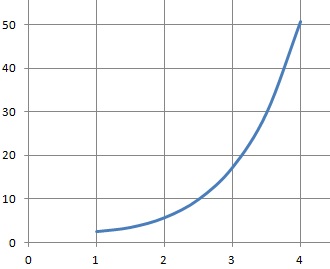
Partie B. Etude de la fonction g
suur [1 ; +oo[.
1. Vérifier que
pour tout réel x, e2x-ex-2=(ex-2)(ex+1).
(ex-2)(ex+1)=e2x+ex-2ex-2
=e2x-ex-2
2. En
déduire une expression factorisée de g'(x).
g'(x) =ex-1-2e-x=
e-x(e2x-ex-2) = e-x(ex-2)(ex+1).
3. On admet que ex-2
>0.
Etudier le sens de variation de la fonction g.
e-x et -x(ex-2)
et ex+1 sont
positifs ;
La dérivée étant strictement positive, la fonction g(x) est strictement
croissante sur [1 ; +oo[.
|
|



