Performances
d'une voiture électrique au démarrage, bac SI Métropole 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Les
voitures électriques sont réputés pour être les plus rapides au
démarrage. l'étude de l'évolution de la vitesse au cours du temps est
menée sur la base d'une vidéo du tableau de bord d'une voiture
électrique, départ arrêté, en ligne droite.
Evolution de la vitesse au cours du temps.
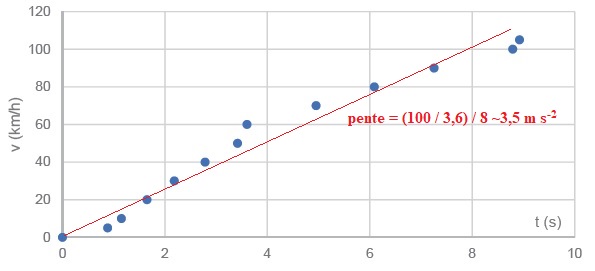
Masse de la voiture : m = 1,6 103 kg.
1. Identifier le référentiel adopté pour les valeurs de la vitesse.
Référentiel terrestre supposé galiléen.
Les constructeurs
caractérisent l'accélération d'une voiture en donnant la durée
nécessaire pour que la voiture atteigne 100 km /h. Pour cette voiture
on mesure une durée de 8,3 s.
2. Déterminer la valeur de l'accélération moyenne.
a = Variation de vitesse / durée de cette variation.
100 km / h = 100 / 3,6 soit 27,8 m /s.
a = (27,8 -0) / 8,3 ~3,3 m s-2.
3.
On choisit de modéliser la dépendance entre la vitesse et le
temps par une relation de proportionalité. Déterminer graphiquement la
valeur de l'accélération de la voiture. Comparer avec la valeur obtenue
à la question 2.
Graphiquement on trouve a = 3,5 m s-2.
Ecart relatif ( 3,5-3,3) / 3,3 =0,06 ( 6 %).
A 6 % près ces valeurs sont en accord.
4.
Déterminer la valeur de la distance nécessaire pour réaliser ce
test. Commmenter en la comparant au contexte quotidien de l'usage d'une
voiture.
v = at, départ à l'arrêt..
La distance est une primitive de la vitesse : d =½at2, la position initiale étant prise comme origine.
d = 0,5 x3,4 x8,32 ~1,2 102 m.
Cette distance est faible, comparée à la distance parcourue chaque jour par une voiture.
5. Déterminer à
accélération constante, par quels facteurs la distance parcourue et la
vitesse atteinte sont divisées lorsque la durée d'observation est
divisée par 2.
La vitesse étant proportionnelle au temps, la vitesse est divisée par 2 si la durée est divisée par 2.
La distance étant proportionnelle au carré du temps, la distance est divisée par 4 si la durée est divisée par 2.
6. Déterminer la valeur de la résultante des forces extérieures exercées sur la voiture.
Seconde loi de Newton : F = ma = 1,6 103 x3,4 =5,4 103 N.
7. Déterminer la
valeur de la variation d'énergie cinétique de la voiture sur un
parcours de 100 m. Représenter les conversions d'énergie mises en jeu
lors de cette phase.
Durée : t = (2d /a)½= (200 / 3,4)½~7,67 s.
Vitesse finale = 3,4 x7,67 ~ 26 m /s.
L'énergie cinétique initiale est nulle ( départ arrêté ).
Variation d'énergie cinétique : ½mv2 = 0,5 x 1,6 103 x262=5,4 105 J.
|
