Mathématiques,
bac STI2D et STL Nlle Calédonie 12 / 2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Exercice
1. QCM 4 points
1. On considère le nombre complexe z = -2.3½+2i. Sa forme exponentielle est :
Le point A d'affixe zA = -1 +i 3½ et le point B a
pour affixe zB = 2 exp(-i 2p / 3).
z = -4 exp(ip /6) ; z = 4 exp(-ip /6) ; z = 2 exp(i 5p /6) ; z = 4 exp(i 5p /6) Vrai.
Module de z : |z| =(12+4)½ = 4.
z / |z| = -3½/ 2+ ½i = cos (5p/6) +i sin (5p/6) ; z = 4 exp(i 5p /6).
2. La fonction f définie sur R par f(t) = 2 sin (3t+p/3) est solution de l'équation différentielle :
2y"+3y=0 ; 2y"+9y=0 ; y"+9y = 0 vrai ; y"+3y=0.
y' =6 cos(3t+p/3) ; y" = -18 sin (3t+p/3).
3. Soit la fonction f définie sur R par f(x) = e-2x et Cf sa courbe représentative. L'équation réduite de la tangente à Cf au point d'abscisse 0 est :
y = -2x+1 vrai ; y = x+1 ; y =-2x-1 ; y = x-1.
f '(x) = -2e-2x ; coefficient directeur de la tangente en x=0 : f '(0) = -2e0 = -2.
y = -2x+b.
Le point de coordonnées (0 ; f(0) = 1) appartient à la tangente.
1 = b ; y = -2x+1.
4. On donne le tableau de variation d'une fonction f :
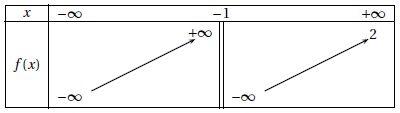
Dans un repère orthonormé, la courbe représentative de la fonction f admet :
- deux asymptotes parallèles à l'axe des abscisses et une asymptote parallèle à l'axe des ordonnées.
- une asymptote parallèle à l'axe des abscisses et une asymptote parallèle à l'axe des ordonnées. Vrai.
- une asymptote parallèle à l'axe des abscisses et aucune asymptote parallèle à l'axe des ordonnées.
- aucune asymptote parallèle à l'axe des abscisses et une asymptote parallèle à l'axe des ordonnées.
Exercice 2. 5 points.
Une entreprise vient d'installer un distributeur à café dans la salle de repos de ses salariés.
Partie A.
On admet que la durée de fonctionnement de ce distributeur jusqu'à l'apparition d'une première panne est de 15 mois.
Ce distributeur bénéficie d'une garantie de 2 ans.
On modélise la durée de fonctionnement, en mois, de ce distributeur
jusqu'à sa première panne par une variable aléatoire T qui suit une loi
exponentielle de variable l.
1. Déterminer la valeur exacte de l.
l = 1 /15 ~0,067mois-1.
2. Dans la suite, on prendra l = 0,067.
a. Calculer la probabilité que ce distributeur n'ait pas subi de panne au cours de 12 premiers mois.
Probabilité que ce distributeur n'ait pas subi de panne au cours de 12 premiers mois: p(T < 12) = 1-e-12 x0,067 =1-0,4475 ~0,553.
b. Calculer la probabilité que ce distributeur subisse sa première panne avant la fin de la garantie.
p(T < 15) = 1-e-15 x0,067 =1-0,368 ~0,632.
Partie B. Les volumes sont exprimés en cL.
La notice précise que le distributeur délivre les cafés dans des
gobelets d'une contenance de 16 cL. Le volume d'un café distribué par
cette machine peut être modélisé par une variable aléatoire X qui suit
la loi normale d'espérance µ =12,5 et d'écart type s = 1,2.
1. Déterminer la probabilité que le volume d'un café soit compris entre 11 cL et 14 cL.
P(X < 11)=0,10565 ; P(X < 14)=0,89435 ;
P(11 < X < 14)=0,89435-0,10565 ~0,789.
2. Déterminer la probabilité que le café déborde du gobelet.
P(X > 16) = 1-P(X <16) =1-0,998 ~0,002.
Partie C.
Tous les cafés délivrés par ce distributeur ont une température initiale de 80°C.
On s'intéresse à l'évolution de la température des cafés servis.
On note q(t) la température d'un café en °C, à l'instant t exprimé en minute.
On admet que la fonction q, définie et dérivable sur [0 ; +oo[ est solution de l'équation différentielle :
q'(t) +0,2 q(t) = 4. (E).
1. Déterminer les solutions de cette équation différentielle.
Solution générale de q'(t) +0,2 q(t) =0.
y = A e-0,2t avec A une constante.
Solution particulière de (E) : y =20.
Solution générale de (E) : y = A e-0,2t +20.
2. Montrer que, pour tout réel t positif : q(t) = 60 e-0,2t+20.
q(0) = A e0+20 = 80 ; A e0 = 60 ; A = 60.
3. Un salarié se sert un café et attend 4 minutes avant de le boire.
a. Quelle est alors la température de son café ?
q(4) = 60 e-0,2*4+20 ~47°C.
b.
Déterminer la valeur exacte de la durée d'attente nécessaire pour que
la température du café atteigne 40°C, puis en donner une valeur
approchée arrondie à la minute.
40= 60 e-0,2t+20 ; 20 = 60 e-0,2t ; 1 /3 = e-0,2t ; ln(1 / 3) = -0,2t ; t = ln(3) / 0,2 ~ 5,493 soit 5 minutes 30 s.
|
...
|
....
|
Exercice 3. 5 points.
La population de loutres d'Europe décroît en France du fait de la
dégradation de son milieu naturel, mais également parce que cette
espèce est victime de pièges posés par les chasseurs.
Partie A.
Cette
population comptait 50 000 individus au premier janvier 1930. Depuis
cette date, la population a perdu 5 % de ses individus chaque année du
fait de la dégradation de son milieu naturel.
1. Calculer la population de loutres au 1er janvier 1931.
50 000 (1-5 /100 = 50 000 x0,95 =47 500.
On
fait l'hypothèse qu'en plus de la chute démographique due à la
dégradation du milieu naturel, 68 individus sont piégés tous les ans
entre le 1er janvier et le 31 décembre. On modélise la population de
loutres par la suite (un) définie par :
u0 = 50 000 et pour tout entier naturel n, un+1 = 0,95 un -68.
2.
Calculer u1 et u2 et interpréter.
u1 = 50 000 x0,95-68 =47 432 loutres au 31 décembre 1931.
u2 = 47 432 x0,95-68 =44 992 loutres au 31 décembre 1932.
3.L'algorithme
suivant permet d'estimer l'année à partir de laquelle la population de
loutres comptera moins de 1000 individus. Compléter cet algorithme.
N <-- 1930
U <-- 50 000
Tant que U > 1000
N <--N+1
U <-- U*0,95-68
Fin Tant que
4.
L'espèce est en danger d'extinction si elle comporte moins de 1000
individus. Justifier qu'un plan de réintroduction ait été mis en place
à partir de 1991.
La population de loutres sera inférieur à 1000 la 61ème année soit en 1991, d'où la mise en place d'un plan de réintroduction.
Partie B.
A partir de 1991, la population de loutres diminue toujours de 5 % par an, mais le plan de sauvegarde prévoit :
- l'interdiction de la pose de pièges :
- la réintroduction de 250 jeunes loutres au 31 décembre de chaque année.
On suppose que la population de loutres est égale à 1000 au 1er janvier 1991.
On modélise la population à partir du 1er janvier 1991 par la suite (vn) définie par :
v0 = 1000 et pour tout n entier naturel n, vn+1 = 0,95 vn +250.
1. Soit la suite (wn) définie par wn = vn-5000.
Justifier que la suite (wn) est géométrique de raison 0,95. Préciser w0.
wn+1 = vn+1-5000 =0,95 vn +250-5000 =0,95 vn+4750=0,95(vn+5000) = 0,95 wn.
w0 = v0-5000 = 1000 -5000 = -4000.
2. Exprimer wn en fonction de n.
wn = w0 *0,95n = -4000 *0,95n.
3. En déduire que vn = 5000 -4000 *0,95n.
vn = 5000 +wn =5000 -4000 *0,95n.
4.
Dans l'hypothèse où l'on conserve la même évolution tous les ans, la
population de loutres peut-elle à long terme retrouver l'effectif de
1930 ? Justifier.
Quand n devient très grand, 0,95n tend vers zéro et vn tend vers 5000.
A long terme la population de loutres tend vers 5000. On ne retrouvera pas la population de 1930.
Exercice 4. 6 points.
Cf est la représentation graphique de la fonction f définie sur ]0 ; +oo[ par : f(x) =ax+bx ln(x).
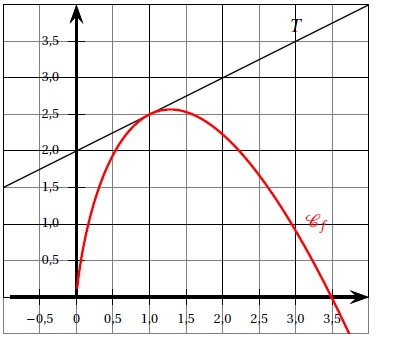
a et b sont deux réels. La droite T est la tangente à Cf au point d'abscisse 1.
Partie A.
1. Déterminer graphiquement f(1) et f '(1).
f(1) = 2,5 ; f '(1) = coefficient directeur de T= 0,5
2. Vérifier que f '(x) = a+b+b ln(x).
Dérivée de bx ln(x). : on pose u = bx et v = ln(x) ; u' = b ; v' = 1 /x.
u'v+v'u = b ln(x) +b.
f '(x) = a +b +b ln(x).
3. En déduire a et b.
f '(1) = 0,5 = a+b ; f(1) = 2,5 =a ; b = -2.
Partie B.
On admet que pour tout réel x de ]0 ; +oo[, f(x) = 2,5 x-2x ln(x).
1. Donner l'expression de f '(x).
f '(x) = a+b+b ln(x) = 2,5-2-2ln(x) =0,5 -2 ln(x).
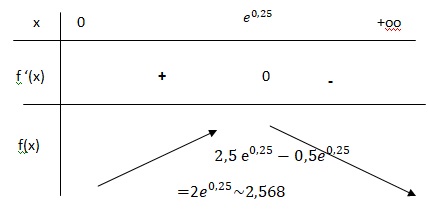
2 Etudier le signe de f '(x) et en déduire le tableau de variation de f. Les limites aux bornes ne sont pas demandées.
f '(x) =0 si : ln(x) = 0,25 ; x = e0,25.
Si x < e0,25; f '(x) >0 et f(x) est croissante.
Si x > e0,25; f '(x) < 0 et f(x) est décroissante.
Partie C.
On souhaite fabriquer des abris à vélos couverts. On a besoin de connaître l'aire des faces latérales.

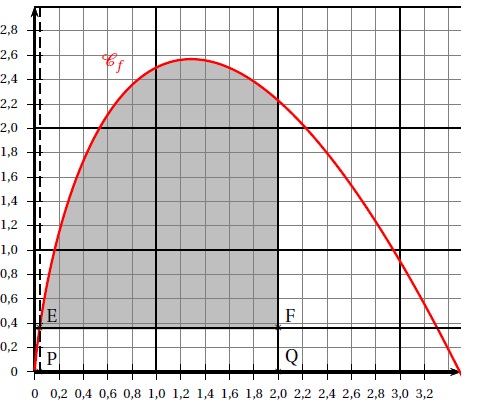
Soit E le point de Cf d'abscisse 0,04 et F le point
d'abscisse 2 ayant même ordonnée que E. Une face latérale est
représentée par le domaine délimité par la courbe Cf, les droites d'équation x = 0,04 et x = 2 et la droite (EF) parallèle à l'axe des abscisses.
1. Montrer que la fonction G définie sur ]0 ; +oo[ par G(x) =x2(1,75 -ln(x)) est une primitive de f.
On dérive g(x) en posant u = x2 et v = 1,75 -ln(x) ; u' = 2x et v' = -1 /x.
u'v+v'u =2x(1,75-ln(x)) -x =2,5 x-2x ln(x) = f(x).
2. On souhaite calculer 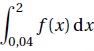 . .
a. Parmi les propositions suivantes, quelle est celle qui permet de calculer cette intégrale ?
f(2) -f(0,004) ; G(2)- G(0,04) vrai ; f(0,04-f(2) ; G(0,04)-G(2).
b. Donner une valeur approchée de cette intégrale.
G(2) =22(1,75 -ln(2))~4,227 ; G(0,04) =0,042(1,75 -ln(0,04))~ -0,00235.
G(2)-G(0,04)~ 4,2.
3. Toutes les dimensions sont exprimées en mètre. En déduire une valeur approchée de l'aire d'une face latérale.
Aire du rectangle EFPQ : (2-0,04) *f(0,04) =1,96 *(2,5 *0,04-0,08 ln(0,04))~ 0,70.
Aire d'une face latérale : 4,2-0,7 ~3,5 m2.
|
|