Lancer de gerbes de paille, Bac Amérique du Nord 2021. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. .. .. . . .. .. ...... ... Le but du jeu est de lancer, à l'aide d'une fourche, une gerbe de paille assimilable à un parallélépipède rectangle de longueur 0,60 m , de largeur 0,40 m et de hauteur 0,40 m au dessus d'une barre horizontale placée à une hauteur précise. Etude du lancer. 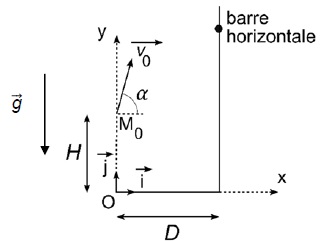La gerbe de masse m = 7,257 kg est assimilable à un point matériel M, correspondant au centre de masse. A l'instant initial, M se trouve en M0, tel que H = 2,80 m. D =2,0 m. a = 80° ; v0 =9,0 m/s. La barre horizontale est à une hauteur de 4,5 m par rapport au sol. L'action de l'air est négligée. A.1. Déterminer les coordonnées du vecteur accélération de M. M est en chute libre : ax = 0 ; ay = -g. A.2. Montrer que les équations horaies du mouvement sont : x(t) = v0 cos a t et y(t) = -½gt2 + v0 sin a t + H. Le vecteur vitesse est une primitive du vecteur accélération. vx= v0 cos a ; vy =-gt +v0 sin a . Le vecteur position est une primitive du vecteur vitesse et M0(0 ; H). x(t) = v0 cos a t ; y(t) = -½gt2 + v0 sin a t + H. A.3 .En déduire l'équation de la trajectoire. t = x / ( v0 cos a) ; repport dans y : y = -½gx2 / ( v0 cos a)2+ x tan a + H. A.4. La gerbe franchira t-elle la barre. y = -0,5 x9,8 x2 / ( 9 cos 80)2+ x tan 80 + 2,8. y = -2,0 x2  +5,67 x +2,8. y(2) = -2,0* 22  +5,67 *2 +2,8 = -8+11,34 +2,8 =6,14 m. Valeur supérieure à 4,5 m, la gerbe passe au dessus de la barre. On s'intéresse à trois positions particulières de M sur sa trajectoire parabolique : la position initiale, le sommet M1 et le point M2 situé à la même hauteur que M0. 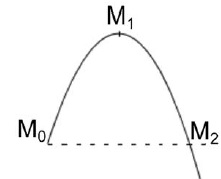L'origine de l'énergie potentielle de pesanteur est prise au sol. A.5. Calculer la valeur de l'énergie cinétique  et celle de l'énergie potentielle de pesanteur en M0. ½mv02 =0,5 x 7,257 x9,02 =293,91 J. mg H = 7,257 x 9,8 x 2,8 =199,13 J. A.6. Indiquer par un raisonnement détaillé si chacune des propositions suivantes est vraie ou fausse, lorsque l'on néglige la résistance de l'air. Proposition I. L'énergie mécanique est maximale en M0. Vrai. En absence de frottement ( chute libre dans ce cas), l'énergie mécanique reste constante. Proposition II. L'énergie cinétique est nulle en M1. Faux. Au sommet de la parabole, seule la composante verticale de la vitesse est nulle. La composante horizontale de la vitesse n'étant pas nulle, l'énergie cinétique n'est pas nulle en M1. Proposition III. L'énergie cinétique en M2 est inférieure à l'énergie cinétique en M0. Faux. Energie mécanique en M0 : mgH + Ec(M0). Energie mécanique en M2 : mgH + Ec(M2). Conservation de l'énergie mécanique :mgH + Ec(M0) = mgH + Ec(M2). Ec(M0) =  Ec(M2). En réalité, l'action de l'air ne peut être négligée. A.7. Indiquer par un raisonnement détaillé si les propositions précédentes restent vraies ou fausses. Proposition I. L'énergie mécanique est maximale en M0. Vrai. L'énergie mécanique diminue du travail des frottements au cours du mouvement. Proposition II. L'énergie cinétique est nulle en M1. Faux. Proposition III. L'énergie cinétique en M2 est inférieure à l'énergie cinétique en M0. Vrai. Energie mécanique en M0 : mgH + Ec(M0). Energie mécanique en M2 : mgH + Ec(M2). Non conservation de l'énergie mécanique : mgH + Ec(M2) < mgH + Ec(M0). Ec(M2) <  Ec(M0).

menu