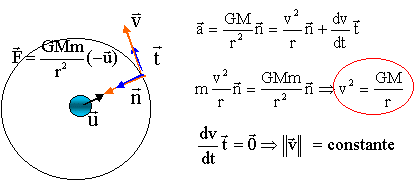Satellites
Starling, nuisances sonores d'un drône, refroidissement d'un bloc de
métal, spécialité SI 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
...
|
.
.
|
..
..
......
...
|
Déploiement
des satellites Starlink.
Ce projet vise à fournir un accès Internet à la
totalité de la
population mondiale grâce à une flotte de plusieurs milliers de
satellites, plats et compacts, ils n'utilisent qu'un seul panneau
voltaïque. Ils sont dotés de 4 antennes puissantes, assurant un fort
débit.
D'après Starlink.com, wikipédia et futura-sciences.
Ils sont transportés dans une fusée Falcon 9, puis déployés les uns
derrière les autres à une altitude d'environ 400 km. Ils rejoignent
ensuite leur orbite finale en utilisant leur propulseur ionique.
L'exercice porte sur l'étude du mouvement d'un satellite Starlink.
Les satellites sont largués de manière à se suivre les uns derrière les
autres. Ils forment ainsi dans le ciel un segment de points lumineux
appelé "train". On suppose pour simplifier que le mouvement des
satellites est rectiligne uniforme pendant la durée d'observation. Le
cercle blanc identifie la tête du train.
1. Exploiter les
clichés pour estimer la valeur de la vitesse de le tête du train.

80 km parcourus en 10 s soit 80 / 10 = 8 km / s = 8 103 m
/s..
2. Dans le
référentiel géocentrique, le mouvement d'un satellite est circulaire,
de rayon r, à la vitesse v.
Faire figurer la base de Frenet et donner l'expression du vecteur
accélération dans ce repère.
3. Etablir que le
mouvement circulaire est uniforme.
4. Donner
l'expression de sa vitesse.
Calcul de la vitesse pour
une altitude h= 380 km.
r = Rterre + h = 6371 + 380 = 6751 km = 6,751 106
m.
Mterre = M = 5,97 1024 kg ; G = 6;67 10-11
SI.
v2 = GM / r =6,67 10-11 x5,97 1024 /
(6,751 106)=5,89 107 .
v = 7,68 103 m /s.
5. Proposer au moins une raison
permettant d'expliquer un éventuel écart entre les valeuurs trouvées
aux questions 1 et 4.
Ecart relatif : ( 8-7,68) / 7,68 ~0,04 ( 4 %).
L'orbite du satellite n'est pas parfaitement circulaire.
Au cours de sa révolution, un satellite n'utilise pas son propulseur,
son mouvement est simplement assujetti à la gravitation et il vérifie
la 3è loi de Kepler.
T2 = 4 p2
/(GM) r3 avec T sa période et r, rayon de l'orbite.
6. Rappeler les
conditions pour qu'un satellite soit géostationnaire. Indiquer si le
satellite Starlink est géostationnaire.
Le plan de l'orbite doit être le plan équatorial terrestre et le rayon
de l'orbite vosin de 42 000 km.
Le satellite Starlink n'est pas
géostationnaire.
Le propulseur est un propulseur au krypton, moins performant que le
propulseur au xénon, mais dix fois moins coûteux.
Le système ( satellite et équipement ) subit une force appelé force de
poussée liée à l'éjection des atomes par le propulseur.
7. Comparer la
force ionique électrostatique exercée sur un ion krypton Kr+
avec celle exercée par les mêmes grilles portées au mêmes potentiels
sur un ion xénon Xe+.
Masse des atomes : xénon : mXe = 2,2 10-25 kg ;
krypton : mKr = 1,4 10-25 kg.
La charge des ions étant la même ; les grilles étant portées au mêmes
potentiels :
La force ionique électrostatique exercée
sur un ion krypton Kr+ est identique à celle excercée sur un
ion xénon Xe+.
On considère que le nombre d'ions xénon éjectés par seconde est
identique à celui d'ions krypton.
8.
En raisonnant sur les masses des ions d'une part et sur les masses des
carburants d'autre part, discuter qualitativemennt l'intérêt de
l'utilisation d'un moteur au xénon par rapport à un moteur au krypton.
L'argon
et le krypton ont des énergies de première ionisation plus élevées que
celle du xénon.
De
plus l'argon et le krypton ont une masse atomique inférieure à celle du
xénon.
L'énergie
cinétique acquise par l'ion à la sortie des grilles est proportionnelle
à la masse de cet ion.
Influence d'un écoulement d'air sur le
refroidissement d'un bloc de métal.
On
mesure au cours du temps l'évolution de la température intérieure d'un
cylindre de cuivre suspendu à l'air libre, avec et sans ventilation.
le bloc de cuivre préalablement chauffé en énviron 50 °C est suspendu à
un fil. Une sonde mesure la température à l'intérieur. Un ventilateur
est posé à proximité du bloc de cuivre. La température de la pièce est
environ 20 °C.
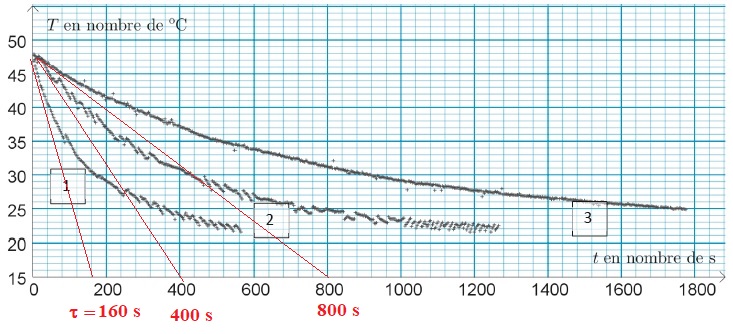
Selon le mode de fonctionnement du ventilateur, on obtient les
résultats suivants.
Modélisation du flux
thermique au cours du refroidissement.
Le cylindre est le système d'étude. Sa variation d'énergie interne
entre les instants t et t+Dt
très proches est U(t+Dt)-U(t)
= h S (Text-T(t))Dt.
S : aire de la surface extérieure du cylindre, Text :
température de la pièce ; t(t) température du cylindre de cuivre et h
le coefficient conducto-convectif.
Masse du cylindre m = 177 g ; hauteur du bloc l = 3,0 cm ; rayon
du cylindre : R = 1,5 cm ;
capacité thermique du cuivre C = 385 J kg-1 K-1.
1. Associer, en
justifiant, chacune des courbes 1, 2 et 3 à la situation correspondante
:
a : absence de ventilation.
La convection autour du cuivre est faible, le bloc se refroidit
lentement (courbe 3).
b : ventillation modérée.
L'air frais ( 20°C) est renouvelé autour du bloc, la température de
celui-ci diminue plus rapidement ( courbe 2).
c. ventilation forte.
L'air frais ( 20°C)
est renouvelé rapidement autour du bloc, la température de celui-ci
diminue trés rapidement ( courbe 3).
2.
Proposer une interprétation physique du coefficient h et prévoir la
situation pour laquelle sa valeur est la plus élevée.
Ce coefficient quantifie le transfert de chaleur réalisé par un
phénomène de convection au sein d'un fluide en mouvement contre une
paroi chaude ou froide.
Ce coefficient est plus élevé pour une convection forcée ( ventilation)
que pour une convection naturelle.
3. En appliquant le premier principe
de la thermodynamique au bloc de cuivre entre les instants t et t +Dt et en se plaçant à la
limite Dt -->
0, établir l'équation différentielle qui caractérise l'évolution
temporelle du système :
dT(t) / dt = h S / (mC)(Text-T(t)).
Variation d'énergie interne du cuivre :
U(t+Dt)-U(t) = h S (Text-T(t))dt
= m c dT(t).
On pose C = m c exprimé en J K-1.
dT(t) / dt = h S / C (Text-T(t)).
4. Déterminer
en justifiant si l'affirmation suivante est correcte.
" A un instant donné, plus l'écart de température entre le bloc et
l'extérieur est important, plus il se refroidit lentement".
Le flux thermique est proportionnel à la différence de température T(t)
- Text. l'affirmation est fausse.
5. On définit la
grandeur t = C
/(hS).
Déterminer la dimension de t.
C : J K-1 ; h : W m-2 K-1 ; S m2
;
C / (hS) : J W-1 avec W = J s-1.
t
s'exprime en seconde.
6. La solution de
l'équation différentielle s'écrit :
T(t) = Text +(T(0)-Text)e- t / t.
Proposer une interprétation physique de t. Commenter l'allure de la
courbe 1 ( valeur de T(0), valeur de Text, signe de de la
pente et évolution de la pente).
t est
la constante de temps, caractérisant la rapidité d'évolution de la
température du cuivre.
T(0) = 50 °C ; Text ~20°C.
La pente de la tangente à la courbe est négative ; cette pente diminue
au cours du temps.
7. Déterminer la
valeur du coeficient h de la courbe 1. Décrire son évolution pour les
courbes 2 et 3.
dT(t) / dt = - (T(0)-Text)
/ t e- t / t = -30 / t e- t / t .
A l'intant initial,
la pente de la tangente est égale à : -30 / t .
Courbe
1 : t =
160 s ; | pente | =30 / 160 ~0,19.
mc / (hS) = 0,19 ; h = mc /( t
S).
S = 2 p R l =6,28 x1,5 10-2
x 3 10-2 =2,8 10-3 m2.
mc = 0,177 x 385 ~68,1 J K-1.
h = 68,1 /(160 x2,8 10-3)=1,5
102 W
m-2 K-1 .
Courbe 2 : t = 400 s ; | pente | =30 /
400 ~0,075.
h = 68,1 /(400
x2,8 10-3)=61 W m-2 K-1 .
|
|
....
|
Nuisances sonores d'un drone.
Le niveau d'intensité sonore en vol ne doit pas dépasser 85 dB à 1 m de
distance.
Lors d'un spectacle de drones, plusieurs centaines de drones défilent à
seulement une trentaine de mètres des spectateurs.
1. Démontrer que le
niveau d'intensité sonore L(dB) est lié à la distance x (m) par la
realtion :
L = 10 log( P /(4pI0)
- 20log (x).
I = P / (4px2)
I / I0 = P /((4pI0)x2)
L = 10 log( P /((4pI0)x2)) = 10
log( P /(4pI0)
+10 log(1/x2) =10 log( P /(4pI0) - 20log (x).
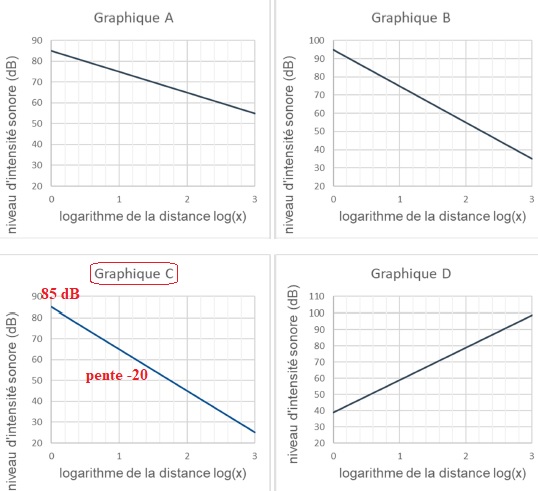
2. Déterminer
parmi les propositions ghraphiques ci-dessous celle qui correspond à la
représentation graphique de la relation précédente.
3. Sélectionner la
bonne réponse en justifiant.
Question 1
: si la distance au drone double, comment évolue le niveau
d'intensité sonore ?
a) Le niveau d'intensité sonore est augmenté de 20 dB.
b) Le niveau d'intensité sonore
est atténué de 3 dB.
c) Le
niveau d'intensité sonore est atténué de 6 dB. Vrai.
L = Cste - 20 log x.
Si x double, L diminue de 20 log 2 ~6 dB.
Question 2 : si la
distance au drone est divisée par 10, comment évolue le niveau
d'intensité sonore ?
a) Le niveau d'intensité sonore est augmenté de 10 dB.
b) Le niveau d'intensité sonore
est atténué de 10 dB.
c) Le
niveau d'intensité sonore est augmenté de 20 dB. Vrai.
L = Cste - 20 log x.
Si x est divisé par 10, L augmente de 20 log 10 = 20 dB.
4.
Montrer que la valeur de P est voisine de 4 mW.
L = 10 log( P /(4pI0)
- 20log (x).
Pour x = 1, L = 85 dB.
85 = 10 log( P /(4pI0).
8,5 = log( P /(4pI0).
108,5 = 3,16 108 = P /(4pI0).
P = 3,16 108 x4 x3,14 x10-12 =3,97 10-3 W ~4 mW.
5. Déterminer à
l'aide du graphique C, la distance du drone pour laquelle le niveau
d'intensité sonore perçu par une personne est équivalent à celui d'une
chambre à coucher.( 30 dB).
Comparer cette distance à la hauteur imposée par la réglementation.
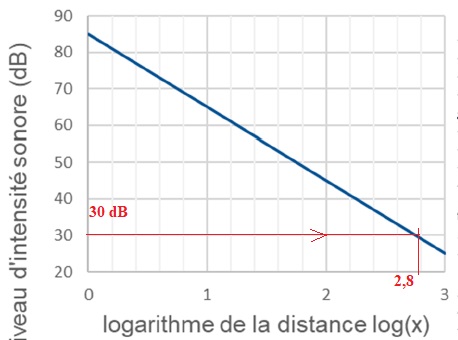
102,8 ~631 m.
20 fois la distance de 30 m imposée par la législation.
6. Un spectacle
utilise 500 drones volant en essaim à une distance moyenne des
spectateurs de 30 m. Déterminer dans ces conditions, si les spectateurs
ont besoin de protection auditives.
Puissance totale : 500 x 4 10-3 = 2 W.
I = P / (4px2) = 2 /(4 x3,14 x302)=1,77 10-4 W m-2.
L = 10 log( 1,77 10-4 / 10-12) =82 dB, valeur inférieure au seuil de risque ( 85 dB).
A partir de quel nombre de drones
volant à 30 m des spectateurs, cela représente-t-il un risque ?
Commenter.
L = 85 dB ; I = 10-12 x 108,5 =10-3,5 ~3,16 10-4 W m-2.
P = 4 px2 I =4 x3,14 x3,16 10-4 x302 =3,57 W.
Nombre de drones : 3,57 / (4 10-3) ~893.
Le ciel est très encombré, le risque de collisions est grand.
.
|
|