Mathématiques
BTS groupe A 09/20.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Exercice 1.
Un technicien décide d'insérer en amont du variateur une inductance de ligne.
A. Etude du modèle théorique.
On note i1 la fonction définie et dérivable sur [0 ; +oo[
qui modélise le courant ( A) induit dans cette inductance en fonction
du temps t (s). A t=0, i1(0) = 0. L'équation régissant l'évolution du courant i1 dans le circuit est :
Ldi1/dt +Ri1 = E.
L : inductance (H), R : résistance (ohm), E= 6 V : différence de potentiel dans le circuit ( V).
Dans cette partie R = 0,5 ohm, L = 0,015 H.
1. Justifier que la fonction i1 est solution de l'équation différentielle (E1) 3y'+100y = 1200.
0,015 i'1 +0,5 i1 = 6 ; diviser par 0,005 : 3 i'1+100 i1=1200.
2.
On rappelle que l'équation différentielle ay'+by = 0 ( a et b réels et
a non nul) admet pour solution : y(t) = K exp(-b/ a t), avec K
constante réelle.
a. Donner les solutions de l'équation différentielle (E0) 3y' +100 y =0.
y = K exp(-100 t / 3).
b. Déterminer une fonction constante y0, solution particulière de (E1).
y0 = 12.
c. En déduire les solutions de (E1).
y = K exp(-100 t / 3) +12.
3. Montrer que pour tout réel positif ou nul : i1(t) = 12-12 exp(-100 t / 3).
i1(t) = K exp(-100 t / 3) +12 et i1(0) = 0.
0 = K+12 ; K = -12.
i1(t) = 12-12 exp(-100 t / 3).
4. On note i'1 la fonction dérivée de i1. Calculer i'1(t) et en déduire que la fonction i1(t) est croissante sur [0 ; +oo[.
i'1(t) =1200 / 3exp(-100 t / 3) = 400exp(-100 t / 3).
exp(-100 t / 3) est strictement positif ; i'1(t= >0 et i1(t) strictement croissante.
5. On a tracé la courbe G qui représente la fonction i1. On note T la tangente à cette courbe en son point d'abscisse x = 0.
a. Déterminer une équation de la droite T et tracer cette droite sur le graphique.
Coefficient directeur de T : i'1(0) =400.
Le point de coordonnées (0 ; 0) appartient à T.
Equation de T : y = 400 t.
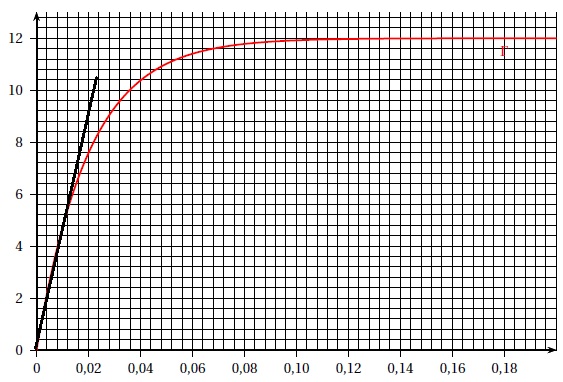
B. Contrôle des valeurs de R et de L.
Sur le schéma ci-dessous, la courbe C représente l'intensité du courant enregistrée. La droite (D) représente la tangente à C en t = 0. Le point de coordonnées (0,02 ; 12) appartient à D.
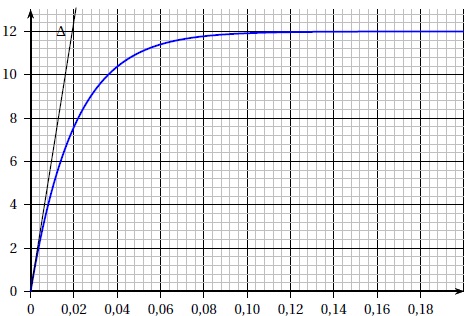
On admet que i2(t) = E/R(1-exp(-R / L t))
1.a. Conjecturer graphiquement la limite de la fonction i2 quand t --> +oo.
Quand t tend vers plus l'infini, i2 tend vers 12 A.
1.b. Montrer que R =0,5 ohm.
exp(-R / L t)) tend vers zéro quand t tend vers plus l'infini et i2(t) tend vers E / R.
E / R = 12 ; R = E /12 = 6 /12 = 0,5 ohm.
2.a Justifier que la droite D a pour équation y = 600 t.
Equation de cette droite passant par l'origine : y = at.
Le point de coordonnées (0,02 ; 12) appartient à D.
12 = 0,02 a ; a = 12 /0,02 =600.
b. Déterminer i'2 (t) puis i'2(0) en fonction de E et L. En déduire la valeur de L.
i'2(t) = E / L exp(-R / L t)) ; i'2(0) = E / L = 600.
L = E /600 = 6 / 600 = 0,01 H.
C. Vérification de la norme.
On note j le nombre complexe de module 1 et d'argument p / 2.
L'inpédance complexe de l'inductance en ligne est Z = R+jLw.
R = 0,5 ohm ; L = 0,01 H et f = 50 Hz.
1. Calculer le module de Z.
w = 2 p f = 6,28 x50 = 314 rad /s.
|Z| =(R2+(Lw)2)½ =(0,25+3,142)½ =3,18 ohms.
2. Le réseau est alimenté par une tension de 230 V. La chute de tension U aux bornes de l'inductance est donnée par U = |Z| Ieff.
Ieff = 3,5 A. La chute de tension U doit être comprise entre
3% et 5 % de la tension d'alimentation du réseau. La chute de tension
est-elle conforme ? Justifier.
U =3,18 x3,5 =11,1 V.
11,1 / 230 x100 = 4,8 %. Donc conformité.
|
...
|
....
|
Exercice 2.
A. Une entreprise fabrique différents modèles d'ampoules LED.
1. Les
ampoules LED MR0011 de 3 W ont une durée de vie annoncée égale à 35 000
heures. On modélise cette durée de vie par une variable aléatoire D
suivant une loi normale de moyenne µ = 35 000 et d'écart type s = 1000.
a. On donne 3 graphiques. L'un des trois représente la fonction densité de la variable D et, en gris, la probabilité P(33 000 < D < 37000). Quel est ce graphique ? Justifier.
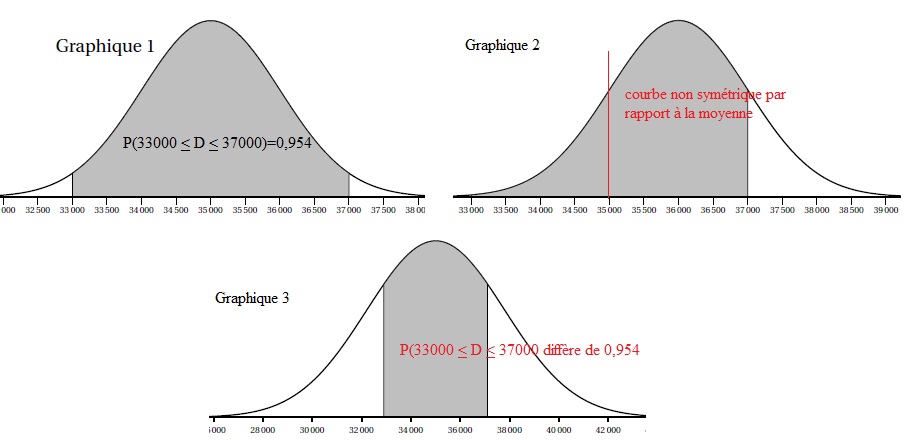
b. Calculer la probabilité qu'une ampoule fonctionne plus de 37 000 h.
P(D > 37000) = 1- P(D < 37000) =1-0,977 = 0,023.
2. L'entreprise fabrique d'autres ampoules ayant les formes suivantes :
20 % sont de forme épi de maïs ;
50 % sont de forme sphérique ;
30 % sont de forme flamme.
90 % des ampoules de forme épi de maïs ont une durée de vie d'au moins 50 000 h ;
30 % des ampoules de forme sphérique ont une durée de vie d'au moins 50 000 h ;
50 % des ampoules de forme flamme ont une durée de vie d'au moins 50 000 h.
On prélève au hasard une ampoule dans la production. On considère les événements suivants :
E : forme épi de maïs ;
S : forme sphérique ;
F : forme flamme ;
V : durée de vie d'au moins 50 000 h.
a. Compléter l'arbre pondéré.
b. Calculer P(F n V)=0,3 x0,5 =0,15.
c. Calculer P(V).
d. Calculer PV(E)= P(V n E) / P(V) =0,18 /0,48 =0,375.
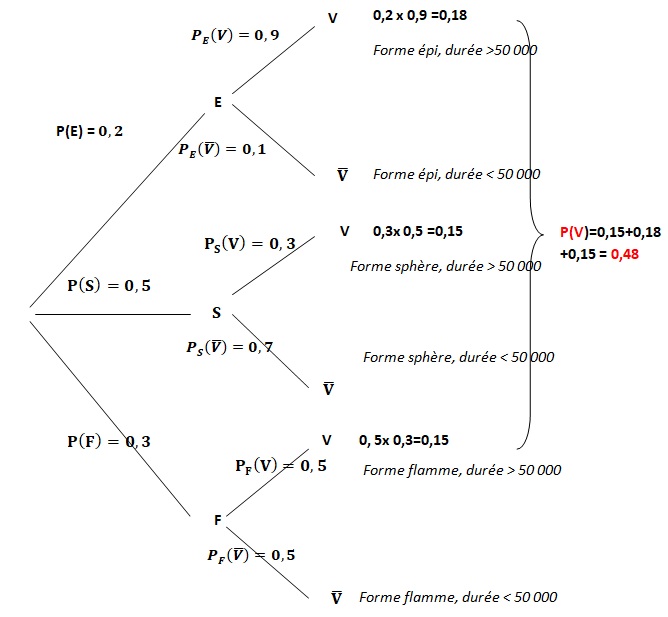
B . La tension simple à la sortie de l'onduleur s'exprime par v(wt), où v est une fonction paire, périodique de période T = 2p et définie par :
v(x) = 300 si 0 < x < p/6 ;
v(x) = 150 si p/6 < x < p/2 ;
v(x) = -150 si p/2 < x < 5 p/6 ;
v(x) = -300 si 5 p/6 < x < p.
1. Compléter la représentation graphique de la fonction v sur l'intervalle [ -3 p/2 ; 3 p/2 ].
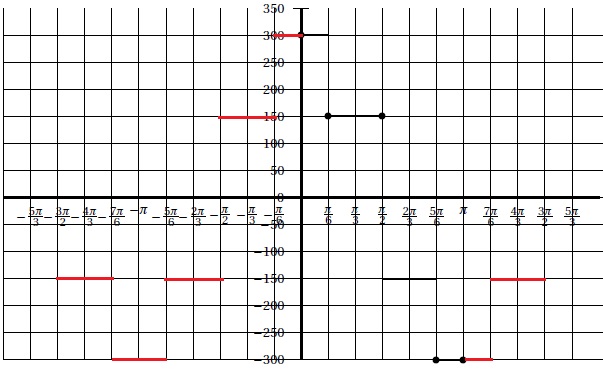
On admet que la fonction v est développable en série de Fourier.
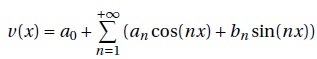
2. Justifier que bn=0 pour tout entier n > 1.
v est une fonction paire ; sin(nx) est une fonction impaire ; les termes sin(nx) sont donc nuls.
3. Montrer que a0 = 0.
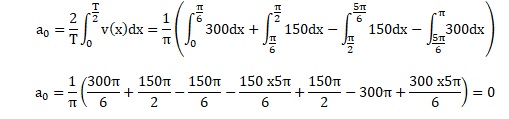
4. Calculer les intégrales suivantes :
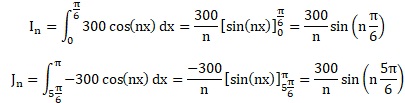
Ecrire les intégrales qu'il reste à calculer pour obtenir l'expression de an en fonction de n. On ne demande pas de les calculer.
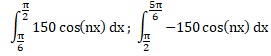
5. On admet que pour tout entier n > 1, on a an = 300 / (np) [sin ( np/6) +2sin (np/2) +sin(5np/6)]. Compléter le tableau :
valeur de n
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
valeur approchée de an
|
0
|
286,5
|
0
|
0
|
0
|
57,3
|
0
|
-40,9
|
6.a. Compléter le spectre des amplitudes An associé à la fonction v pour n allant de 0 à 7.
An = (an2+bn2)½.
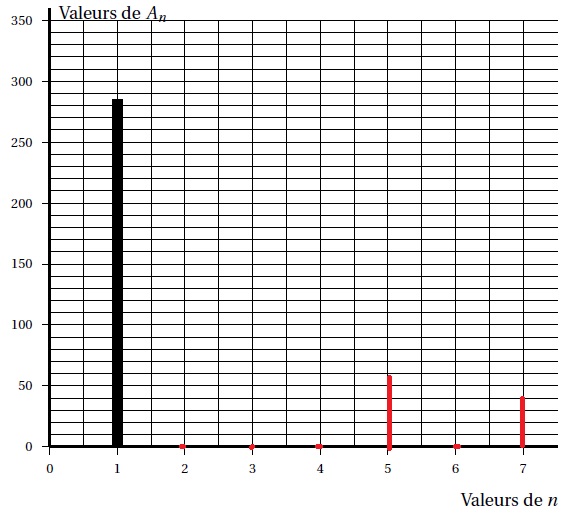
b. Calculer le taux de distorsion T =(a22+a32+a42+a52+a62+a72)½ / a1.
T =(57,32 +40,92)½ / 286,5 =0,24. (24 %)
Cette valeur est supérieure à 10 %, la commande n'est pas adaptée.
|
|