La
physique de l'encensoir de Saint jacques de Compostelle, Agrégation
2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Cet
encensoir de plus de 50 kg constitue un pendule suspendu sous le
transept de la cathédrale. Le pendule est d'abord écarté de sa position
d'équilibre vrticale puis au cours des oscillations, un dispositif
mécanique permet de faire varier la longueur L de la corde qui le
soutient. Sous l'action de 8 tireurs, cette longueur est périodiquement
diminuée puis augmentée de façon à faire croître rapidement
l'amplitude des oscillations du pendule. Les huit hommes tirent sur la
corde qui soulève l'encensoir lorsque celui-ci passe par la verticale
et relâchent la corde quand l'encensoir est au plus haut. les tireurs
augmentent l'énergier d'oscillation du pendule, comme un enfant sur une
balançoire qui s'accroupit et se relève cyclement pour se balancer plus
fort.
1. Grâce à un système à deux tambours, les tireurs soulèvent l'encensoir de Dl = 3 m. Faire un schéma du dispositif et évaluer la valeur Dl'
de la longueur de corde tirée par les hommes. En négligeant le moment
d'inertie du système des deux tambours et la masse de la corde,
exprimer la tension T ' exercée par les hommes sur la corde en fonction
des rayons des tambours ( r' =14,5 cm pour le petit et r =29 cm pour le
grand) et de la norme T de la tension exercée par la corde sur
l'encensoir. Quels sont l'intérêt et l'inconvénient d'utiliser un
système à deux tambours ?
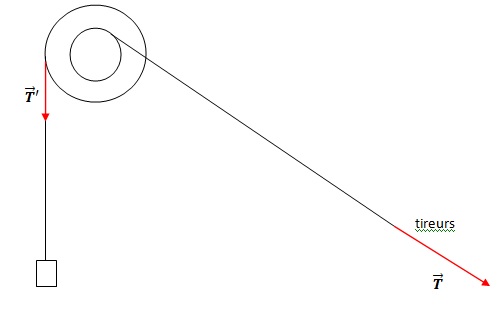
Lorsque les tireurs tirent sur la corde d'une longueur Dl', les deux tambours montés sur le même axe tournent d'un angle a = Dl' / r', la corde des tireurs étant enroulée sur le petit tambour.
La corde de l'encensoir étant enroulée sur le grand tambour, la longueur du pendule diminue de Dl = r a = r / r' Dl'= 2 Dl'=3 m.
Dl'=1,5 m.
Théorème du moment cinétique appliqué au 2 tambours, en projection sur l'axe des tambours : r' T ' - r T = 0.
T ' =r / r' T= 2 T.
Avantage : amplification du raccourcissement du pendule.
Inconvénient : traction plus importante sur la corde.
2. Définir la notion de force centrifuge. Cette force est-elle de même nature que le poids ou la tension de la corde ?
La
force centrifuge apparaît en physique dans l'étude des mouvements des
objets dans des référentiels non inertiel. L'effet ressenti est
dû aux mouvement de rotation : éloignement des corps du centre de
rotation.
La force centrifuge n'est pas de même nature que le poids ou la tension de la corde, car elle dépend du référentiel.
3.
On lit dans le texte : " l'accélération radiale pendant le mouvement de
tirage résulte du déséquilibre entre la tension de la corde, la force
centrifuge et le poids de l'encensoir". Corriger cette affirmation.
Soit O le centre de rotation. Dans le référentiel d'origine O, en rotation à la vitesse angulaire q'
par rapport au référentiel lié à la cathédrale, l'encensoir est soumis
à la tension T de la corde, à son poids P, à la force d'inertie
d'entraînement et à la force d'inertie de Coriolis ( celle-ci ne
possède pas de composante radiale).
Ecrire dans ce référentiel, en projection sur la direction radiale du
mouvement, la loi de quantité de mouvement pour le pendule :
ma'r = mg cos q -T+m r q'2.
q : angle entre la corde et la verticale; T tension de la corde ; m r q'2projection radiale de la force d'inertie d'entraînement.
C'est donc la projection du poids sur la direction radiale du pendule qui intervient.
4. Justifier le signe du travail exercé par la tension de la corde en précisant de quelle énergie il s'agit.
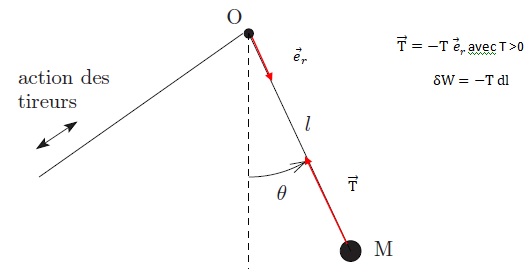
Si la corde est raccourcie, dl < 0 et le travail de la tension est positif ; l'énergie mécanique du pendule augmente.
Si la corde est rallongée, dl >0 et le travail de la tension est négatif.
5.
On note E l'énergie de l'encensoir, l'énergie potentielle étant prise
nulle au point le plus bas de la trajectoire. Evaluer le rapport Wf / E de l'énergie Wf
dissipée par les frottements sur un quart de période ( entre le point
le plus haut et le point le plus bas) sur l'énergie E de l'oscillateur.
Qu'en conclure ?
Position haute : l'énergie mécanique du pendule est sous forme potentielle de pesanteur Ep = mgh avec h = 21 m.
Position basse : l'énergie mécanique du pendule est sous forme cinétique E =½mv2 avec v = 68 km / h soit 68 / 3,6 ~18,9 m /s.
Le travail des frottement correspond à la différence entre ces deux énergies :
Wf = m(gh-½v2) ; Wf / Ep = 1-½v2 / (gh)=1-18,92 /(2x9,8x21) ~0,13.
Il faut donc prendre en compte les frottements de l'air.
6.
Expliquer pourquoi le tirage de la corde introduit une modulation
périodique de fréquence double de celle de l'oscillateur et pourquoi
l'excitation sinusoïdale de fréquence 2 n est moins efficace d'un facteur p / 4 que l'excitation optimale par tirage instantané.
A chaque passage par la position verticale ( deux fois par période ), les tireurs raccourcissent la corde. Le tirage de la corde introduit donc une modulation périodique de fréquence double de celle de l'oscillateur.
Amplitude du premier terme d'une série de Fourier d'un signal en crénaux d'amplitude E : 4 E / p.
Amplitude du premier terme d'une série de Fourier d'un signal sinusoïdal d'amplitude E : E.
L'excitation sinusoïdale de fréquence 2 n est donc moins efficace d'un facteur p / 4 que l'excitation optimale par tirage instantané.
On propose un modèle de l'action optimale des tireurs schématisée ci-dessous :
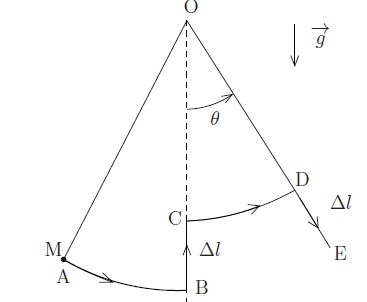
On suppose que par leur action, ils raccourcissent quasi-instantanément la longueur du pendule de Dl lorsque celui-ci passe par la position verticale q=0 entre B et C et qu'ils laissent la corde s'allonger quasi-instantanément de Dl lorsque le pendule a atteint son angle maximal ( entre D et E) et que sa vitesse s'annule. On note l0 la plus grande longueur de la corde et l0-Dl la plus petite longueur avec Dl << l0. La masse de la corde est négligeable devant la masse de l'encensoir. Dans un premier temps on néglige tout frottement.
7. En utilisant le théorème du moment cinétique, donner la relation entre les vitesses de l'encensoir vB en B, vC en C et les longueurs l0 et l0-Dl.
M se situe entre B et C. Entre ces deux points, le moment cinétique en
O se conserve, le poids et la tension étant dirigés suivant OM.
vBl0 = vC(l0-Dl) ; vB =vC(1-Dl / l0).
8. Calculer les variations d'énergie du pendule DEBC entre les points B et C et DEDE entre les points D et E en fonction de m, g, l0, Dl et q. On se limitera à des expressions d'ordre 1 en Dl.
DEBC = ½mvC2 +mg Dl -½mvB2.
Entre C et D l'énergie mécanique reste constante ; de plus vD=0.
½mvC2 = mg (l0-Dl)(1-cos q).
Or vB=vC (1-Dl / l0) ; vB2=vC2 (1-Dl / l0)2 ~vC2 (1-2Dl / l0) .
½mvB2 =½mvC2 (1-2Dl / l0) =mg (l0-Dl)(1-cos q)(1-2Dl / l0).
DEBC = mg (l0-Dl)(1-cos q)+mg Dl -mg (l0-Dl)(1-cos q)(1-2Dl / l0).
DEBC =2 mg (l0-Dl)(1-cos q)(Dl / l0) +mg Dl.
Et en ne gardant que le terme de degré 1 en Dl :
DEBC = mg Dl (3-2cos q).
DEDE = -mgDl cos q,( variation de l'énnergie potentielle), la vitesse étant nulle en D et en E.
|
...
|
....
|
8.
Proposer une démonstration de l'affirmation " Dans ce cas le gain
d'énergie relatif au cours d'une demi-période d'oscillation, est égal
au triple du raccourcissement de la corde, divisé par sa longueur
totale".
Sur un quart de période : DE = DEBC +DEDE = mg Dl (3-2cos q) -mgDl cos q = 3mg Dl (1-cos q).
Energie initiale du pendule en B : E = ½mvB2 =mg (l0-Dl)(1-cos q)(1-2Dl / l0).
E =mg l0 (1-Dl / (l0)(1-2Dl / l0)(1-cos q).
E~mg l0 (1-3Dl / l0)(1-cos q).
DE / E = 3 Dl / [ l0(1-3Dl / l0)]~ 3 Dl / l0(1+3Dl / l0)~3 Dl / l0 à l(ordre 1 en Dl.
Du fait du raccourcissement et de l'allongement successifs de la corde, l'amplitude des oscillations du pendule augmente.
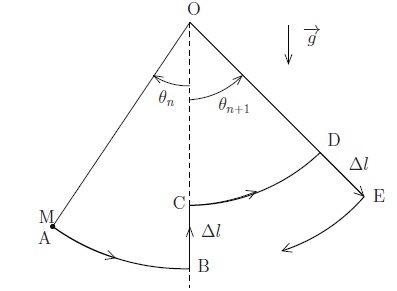
9. Déduire de ce modèle une relation entre les angles maximaux successifs qn et qn+1 et l0 et Dl. Pour cet encensoir, l0 = 21,5 m et Dl
= 3 m. Montrer que ce modèle n'est pas compatible avec les observations
suivantes " Après la poussée initiale, l'amplitude angulaire est de 13°
; après 80 s et 17 demi-périodes, l'amplitude maximale de 82 ° est
atteinte, l'encensoir atteignant un point situé à 0,5 m sous la voûte".
Energie mécanique en A ( vA = 0) : mgl0(1-cos qn).
Energie mécanique en B ( origine énergie potentielle) : ½mv2B.
Conservation de l'énergie mécanique entre A et B : v2B =2gl0(1-cos qn).
Conservation du moment cinétique entre B et C :
vBl0 = vC(l0-Dl).
vC2 =vB2 l02/ (l0-Dl )2=2g l03(1-cos qn) / (l0-Dl )2.
Energie mécanique en D ( vD=0) : mg(l0-Dl)(1-cos qn+1).
Conservation de l'énergie mécanique entre C et D : ½mvC2 = mg(l0-Dl)(1-cos qn+1).
vC2 =2g(l0-Dl) -2g(l0-Dl)cos qn+1 ; vC2 / [2g(l0-Dl)] =1 -cos qn+1.
cos qn+1 =1-vC2 / [2g(l0-Dl)].
cos qn+1 =1- l03(1-cos qn) / (l0-Dl )3.
A.N. cos qn+1 =1- 21,53(1-cos qn) / (18,5 )3=1-1,57(1-cos qn)
q0 =13° ; q1 =16,3° ; q2 =20,5° ; q3 =25,7° ; q4 =32,4° ; q5 =40,9° ; q6 =52° ; q7 =66,6° ; q8 =86,9°.
On atteint 86,9 ° en 8 demi-périodes ( en contradiction avec 82° en 17 demi-périodes).
Ce modèle ne convient pas.
Il faut prendre en compte les frottement sur les couches d'air.
Le raccourcissement de la corde n'est pas instantané.
La vitesse de la corde a également une composante horizontale en B et C.
|
|



