Communications
par ondes électromagnétiques dans la maison,
Capes physique chimie 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Le téléviseur et sa télécommande.
Les deux principales caractéristiques d'une télévision sont la taille
et la définition de son écran. La définition de l'écran correspond au
nombre total de pixels. Les couleurs sont codées en RVB.
21.
Rappeler le principe du codage RVB. Donner les couleurs correspondant
aux codages suivants en justifiant : (255 ; 0 ; 0) ; (0 ; 0 ; 0) ;(255
; 255 ; 0) ; (125
; 125 ; 125 ). Calculer le nombre de couleurs différentes que peut
générer un pixel sur l'écran.
Le
mode de représentation RVB( rouge, vert, bleu ) est le plus utilisé
pour la restitution de l'image. L'image est composée d'une matrice de
points appelés pixels. Un
pixel est composé de trois couleurs ( le rouge, le vert, le bleu). Le
mode de composition des couleurs se fait par addition des couleurs. En
jouant sur l'intensité de chacune d'elle, on peut recréer les autres
couleurs.
(255 ; 0 ;
0) : rouge seul.
(0
; 0 ; 0) : absence de couleur ( noir).
(255 ; 255 ;
0) : rouge et vert avec la même intensité soit le jaune.
(125
; 125 ; 125 ) : gris ( les trois couleurs sont présentes avec la même
intensité )
Une
image numérique est généralemet codée en RVB 24 bits.Un pixel peut génèrer 224 =
256*256*256 = 16 777 216
couleurs différentes.
22.
Une des conceptions initiales des élèves concernant la perception des
couleurs est que la couleur d'un objet est une propriété de l'objet,
elle ne dépend pas de la lumière qui éclaire l'objet. Proposer une
activité permettant de remettre en cause cette conception initiale.
Trois groupes d'élèves possèdent les mêmes objets ce couleurs :blanche,
noire, rouge, vert, bleu, jaune, cyan et magenta.
Le premier groupe éclaire les objets avec une lumière rouge et doit
identifier les objets de couleur rouge.
Le
second groupe éclaire les objets avec une lumière bleue et doit
identifier les objets de couleurs bleue.
Le troisième groupe éclaire
les objets avec une lumière verte et doit identifier les objets de
couleurs verte.
Rassembler les réponses et conclure : la couleur de l'objet dépend de
la lumière qui l'éclaire.
Pour piloter le téléviseur, une télécommande équipée de diodes qui
émettent des ondes électromagnétiques dans l’infrarouge, est utilisée.
23. Définir la
notion d’une onde progressive. Quelle est la principale différence
entre une onde mécanique et une onde électromagnétique ? Justifier que
le rayonnement émis par la télécommande correspond bien à un
rayonnement infrarouge ( fréquence f = 3,19 1014 Hz).
Onde mécanique progressive : propagation d'une perturbation
dans un milieu matériel sans
transport de matière,
mais avec transport d'énergie.
Une onde mécanique nécessite la présence d'un milieu matériel pour se
propager. Une onde électromagnétique peut se propager dans le vide.
Longueur d'onde du rayonnement émis par la télécommande :
l = c / f
=3,0 108 / (3,19 1014) ~9,4 10-7 m =
0,97 µm > 0,8 µm, donc domaine proche IR.
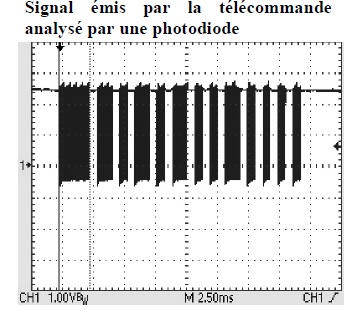
24. Le signal émis par la
télécommande est analysé par une photodiode reliée à un oscilloscope.
Le signal ainsi obtenu peut-il être considéré comme numérique ?
Justifier.
Le signal ne prend que deux valeurs (tension haute = 1 et
tension basse =0). C'est un signal numérique.
Transmission par fibre
optique.
Il est possible d’installer une fibre optique pour optimiser le
débit associé aux communications par le réseau internet.
25. Rappeler une
propriété d’un faisceau laser qui justifie l’usage de ce type de
rayonnement électromagnétique pour la transmission d’information par
fibre optique.
Le
faisceau laser est monochromatique.
On considère que la fibre à saut d’indice utilisée est
constituée d’un coeur cylindrique de rayon a, d’indice n1 =
1,510 et d’une gaine de rayon extérieur b, d’indice n2
= 1,495. Un schéma de cette fibre est donné. Un rayon incident se
propage dans l’air dans un plan axial de la fibre et arrive en I, à une
distance OI < a de l’axe, sur une extrémité de la fibre, sous un
angle d’incidence i0. On note i1 l’angle que fait
le rayon avec la normale séparant la gaine du coeur.
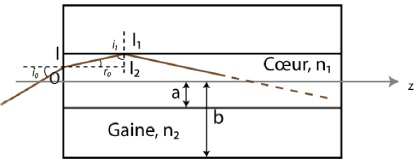
26. Déterminer la
condition sur i1 pour qu’il y ait guidage dans la fibre. En
déduire la condition sur i0, de la forme i0 < im,
permettant le confinement du rayon dans la fibre. On appelle ouverture
numérique O.N la quantité sin(im). Retrouver l’expression de
O.N. en
fonction de n1 et n2 : O.N = (n12
-n22)½. Donner sa valeur
numérique. Commenter.
Relation de Descartes pour la réfraction
en O :
nair sin i0 = n1
sin r0
; sin i0
= n1 sin r0
/ nair ;
Les angles r0 et i1 sont complémentaires.
Il y a guidage dans la fibre si au point I il y a réflexion totale :
n1 sin i1 = n2 sin 90 ; sin
i1 = n2 / n1 =1,495 / 1,510 =0,9900 ; i1
=81,92°.
r0 = 90 -81,92 =8,08° ;
sin
im
= n1 sin r0
/ nair =1,510 sin 8,08 ~0,212.
im = 12,3°.
Si i0 est inférieur à 12,26°, il y a réflexion totale en I
et guidage dans la fibre.
O.N = sin
im
= n1 sin r0
; sin i1 =n2
/ n1 =cos r0
( angle complémentaires).
sin r0 = (1-cos2r0)½=(1-(n2
/ n1)2)½=(n12 -n22)½
/ n1.
O.N = (n12 -n22)½
=(1,512 -1,4952)½ =0,212.
im = 12,3°. le cône d'ouverture est suffisant pour permettre
une réflexion totale et donc un guidage dans la fibre.
27. Un signal de sortie est
exploitable tant que sa puissance Psortie est supérieure à 1
% de la puissance Pentrée
du signal entrant. Au bout de combien de kilomètres faudra-t-il prévoir
une amplification optique intermédiaire pour garder des signaux
satisfaisants en supposant que l’on se place à la longueur d’onde de
1550 nm ( atténuation 0,2 dB / km). Commenter.
Atotale = 10 log ( Pentrée / Psortie)
= 10 log 100 = 20 dB.
Longueur de fibre avant amplification : 20 / 0,2 = 100 km.
|
|
....
|
28. Résolution de problème :
longueur maximale d’une fibre permettant de transmettre un signal sans
recouvrement d’impulsions.
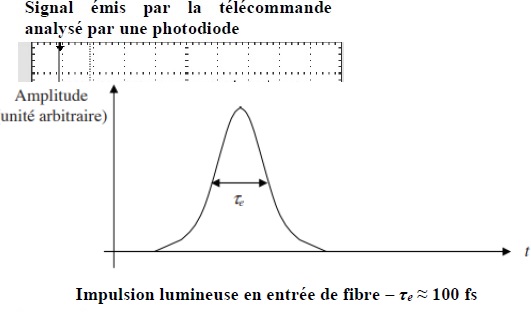
Le codage binaire de l’information consiste à envoyer des
impulsions lumineuses, appelées bits, périodiquement avec une fréquence
f (exprimée en bits par seconde). Ces impulsions lumineuses, de durée τe
de l’ordre d’une centaine de femtosecondes (cf. graphe ci-dessous),
sont formées chacune par un faisceau conique de rayons lumineux, de
demi-angle au sommet im (on peut se référer à la question
26), entrant dans la fibre au point O. Les angles d’incidence étant
différents, les durées associées pour parcourir la fibre sont
différentes.
En estimant la durée d’une impulsion en sortie de la fibre, évaluer la
longueur maximale de fibre que l’on peut utiliser pour transmettre
correctement un signal avec un débit de 100 Mbits.s–1.
Pour une fibre de longueur L et un angle d'incidence ß compris entre 0
et 12 °, la distance parcourue par un rayon lumineux est L / cos ß.
Dispersion d'une impulsion en sortie de fibre :
te+ L/
c [ 1 / cos 12 -1 / cos 0) avec c = 3,0 108 / 1,5 =2,0 108
m /s.
10-13+L / (2 108)[1/0,978-1]= 10-13+L / (2 108)=10-13
+1,12 10-10 L
Pour un débit de 100 Mbits, durée de 1 bit : 1 / (100 106) =
10-8 s .
10-13
+1,12 10-10 L <10-8.
1,12 10-2 L < 1 ; L < 90 m.
Au delà de 90 m, il faut soit réduire le débit, soit modifier la forme
du signal.
|
|


