Mathématiques,
école de santé des armées ESA 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Exercice 1. (6 points)
Une
seule affirmation est exacte. Aucune justification n'est demandée.
Réponse juste = 1 point ; réponse fausse = -0,25 point. Absence de
réponse = 0 point.
QCM 1.
Les solutions réelles de l'équation 3 (ln(x))2 +2 ln(x) -5 =0.
On pose X = ln(x) strictement positif ;
3X2+2X-5 = 0 ; discriminant D = 22+4*5*3=64 = 82.
Solution retenue X = (-2 +8) / 6 =1 ln(x) = 1 soit x = e.
A. {1 ; -5 /3} ;
B. { e ; e-5/3} .
C. { e-5/3}.
D. { e}. Vrai.
QCM 2.
Les solutions réelles de l'inéquation (ex-1)(1-x) > 0 sont :
ex = 1 soit x = 0 et x = 1.
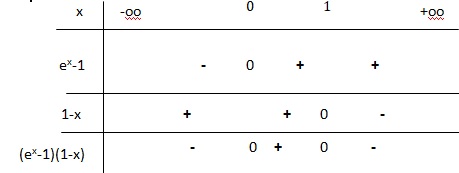
A. ] -oo ; 1 ].
B. [0 ; 1 ] vrai.
C. [0 ;+oo[
D. ] -oo ; 1 ] u [1 ;+oo[ .
QCM 3.
Les solutions réelles de l'inéquation ln(-x+5) < ln(x+1) sont :
-x+5 >0 soit x < 5 et x+1 > soit x > -1.
ln(x-5) -ln(x+1) < 0 ; ln(x-5) /(x+1) < 0.
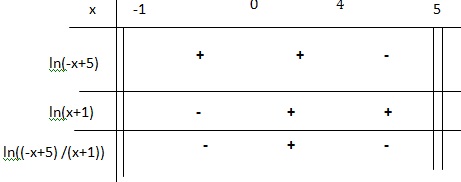
X appartient à ]-1 ; 0[ union ]4 ; 5[.
A. ]2 ; +oo[
B. ]-oo ; 5[
C. ]-1 ; 5[ vrai.
D. ]2 ; 5 [.
QCM 4.
La limite de (x2+1)½-(x2-1)½ en plus l'infini est :
x(1+1/x2)½-x(1-1/x2)½ = x [(1+1/x2)½-(1-1/x2)½ ].
A. +oo
B. 1.
C. 0. Vrai.
D. 2.
QCM 5.
Soit la fonction f définie sur R par f(x) = x exp(x2-1), alors :
On pose u = x et v =exp(x2-1) , u' = 1 et v' = 2x exp(x2-1)
u'v+v'u = exp(x2-1) +2x2 exp(x2-1) =(1+2x2)exp(x2-1)
A. f '(x) = exp(x2-1).
B. f '(x) = 2x exp(x2-1).
C. f '(x) = (1+2x2)exp(x2-1).
Vrai.
D. f '(x) = 2x2exp(x2+1).
QCM 6.
Indication : calculer la dérivée de h(x) =x sin x + cos x.
h '(x) = sin x +x cos x -sin x = x cos x ; h(x) est une primitive de x sin x+ cos x.
L'intégrale I ci-dessous est égale à :

Réponse B.
Exercice 2. ( 6 points).
Pour les QCM 7 et 8, on considère une population dont 5 % est touchée par une maladie.
QCM 7.
On
considère de manière aléatoire et indépendante deux personnes de cette
population. Soit l'événement A : " aucune personne n'est malade". La
probabilité de A est égale à :
Epreuve de Bernoulli ; loi binomiale de paramètre n = 2; p = 0,05 ; q = 1-p = 0,95.
P (X =0) =0,9025.
A. 0,9025.
Vrai.
B. 0,0025.
C. 0,9975.
D. 0,1.
QCM 8.
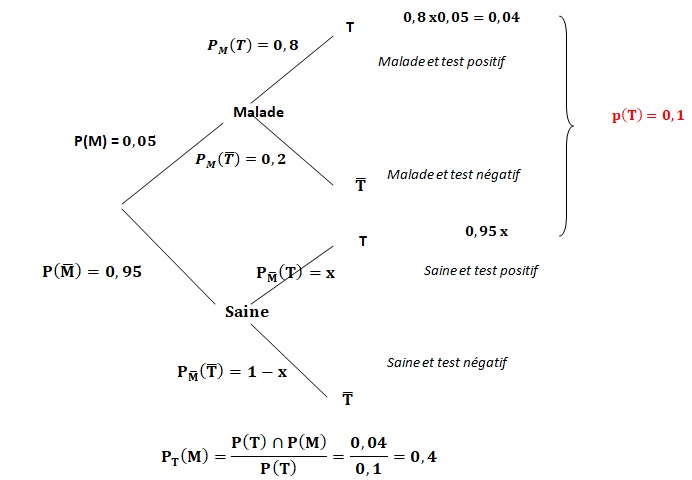
On
sait que la probabilité qu'une personne ait un test positif à cette
maladie, sachant qu'elle est malade, est 0,8. D'autre part, la
probabilité d'avoir un test positif pour une personne de cette
population est 0,1. La probabilité que la personne soit malade
sachant qu'elle a un test positif est égale à :
A. 0,8.
B. 0,01.
C. 0,4. Vrai.
D. 0,04.
QCM 9.
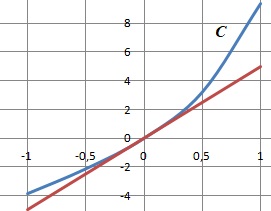
Soit la fonction f définie sur R par f(x) = e2x +3x-1 et C sa courbe représentative. La tangente à C au point d'abscisse 0 a pour équation :
f '(x) = 2e2x+3 ; coefficient directeur de la tangente : f '(0) =5.
Equation de la tangente y =5 x+b.
La tangente passe par le point decoordonnées x =0 ; f(0) =0 ; b = 0.
A. y = 5 x-1.
B. y = 5x. Vrai.
C. y = 4x.
D. y = 5x+3.
QCM 10.
Soit la suite réelle (un) définie par : u0 = 1,5 et un+1 = 2un-1.
A. La suite (un) converge vers 1, abscisse du point d'intersection des droites d'équations y = x et y = 2x-1. Faux.
u1 = 2*1,5-1 =2 ; u2 = 2*2-1 =3 ; u3 = 2*3-1 =5.
B. La suite (vn) définie par vn = un-1 est géométrique. Vrai.
vn+1 = un+1-1 = 2un-2 = 2(un-1)=2 vn.
La suite (vn) est géométrique de raison 2 et de premier terme 0,5.
C. La suite (un) est majorée. Faux.
D. La suite (un) est décroissante. Faux.
QCM 11.
Soit la suite (un) définie par un = n2-10n+1.
A. La suite converge vers 1.
B. La suite diverge vers plus l'infini. Vrai.
C. La suite converge vers zéro.
D. La suite diverge vers moins l'infini.
QCM 12.
La solution y de l'équation différentielle 2y'-y=3 vérifiant y(0) =-1 est définie par :
A. y(x) =e2x-2.
B. y(x) =2e0,5x-3. Vrai.
C. y(x) =2e0,5x-1.
D. y(x) =e2x-3.
Solution générale de 2y'-y=0 : y = A e0,5x avec A une constante.
Solution particulière de 2y'-y=3 : y = -3.
Solution générale de 2y'-y=3 : y = A e0,5x -3.
y(0) =A-3 = -1 ; A = 2.
y = 2e0,5x-3.
|
...
|
....
|
Exercice 3. (8 points).
I.
Un virus sévit dans une population. Un test permet de dire avec
certitude si un individu est malade ou non. Mais il est coûteux et
invasif. Dans la pratique, on met en place un test sérologique, dont
les indicateurs caractéristiques - la sensibilité et la spécificité -
sont définis ci-après.
On prélève un individu au hasard ans la population et on considère les événements :
M : " lindividu est malade ".
NM : " l'individu n'est pas malade".
T+ : " teste positif".
T- : " test négatif".
On note :
p la probabilité que l'individu soit malade, on l'appelle la prévalence de la maladie ;
Se=PM(T+) la sensibilité du test
Sp = PNM(T-) la spécifité du test.
1. Quelques calculs.
Recopier et compléter l'arbre pondéré ci-dessous.
2. On appelle valeur prédictive positive du test le nombre VPP = PT+(M).
Montrer que VPP = Se p /(Se p +(1-p) (1-Sp).
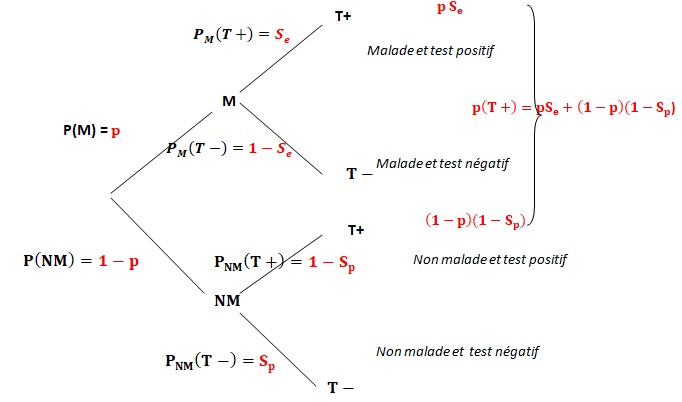
VPP = PT+(M)=Se p /(Se p +(1-p) (1-Sp).
3.
Dans cette question, on suppose que la prévalence est de 30 %, que la
sensibilité du test est de 90 % et que la spécificité du test est de 90
%.
a. Calculer VPP.
b. Le test a t-il un intérêt ?
Se =0,9 ; p =0,3 ; Sp = 0,9.
VPP = Se p /(Se p +(1-p) (1-Sp)= 0,9 x0,3 /(0,9 x0,3 +0,7 x 0,1) =0,27 / 0,34 ~0,79 ( 79 %).
La valeur prédictive positive est de 79 % : le test a un intérêt.
4. Dans
cette question, on suppose que la prévalence est de 1 %, que la
sensibilité du test est de 90 % et que la spécificité du test est de 90
%.
a. Calculer VPP.
b. Le test a t-il un intérêt ?
c. Quel probléme se pose en cas de maladie rare ?
Se =0,9 ; p =0,01 ; Sp = 0,9.
VPP = Se p /(Se p +(1-p) (1-Sp)= 0,9 x0,01 /(0,9 x0,01 +0,99 x 0,1) =0,009 / 0,099 ~0,09 ( 9 %).
La valeur prédictive positive est de 9 % : le test a peu d'intérêt.
Dans le cas d'une maladie rare, la VPP est faible. Un patient
réagissant positivement au test a une faible probabilité d'être atteint
par la maladie. Des examens complémentaires doivent être envisagés.
5.
La VPP d'un test sérologique n'est pas toujours un indicateur
satisfaisant. On s'intéresse alors àun autre indicateur, le ratio de
vraisemblance positif du test, défini par : RV+ =PM(T+) / PNM(T+)
a. Exprimer RV+ en fonction des indicateurs du test.
PM(T+) = Se ; PNM(T+)= 1-Sp. RV+ = Se /(1-Sp).
b. Calculer RV+ avec les données de la question 3 puis celles de la question 4.
Question 3 : RV+ =0,9 /0,1 = 9.
Question 4 : RV+ =0,9 /0,1 = 9.
c. On admet que plus RV+ est grand, plus la VPP est grande.
D'après la question précédente, le RV+ est-il suffisant pour conclure à
la fiabilité du test ? Si on a plusieurs tests possibles, comment
choisir Se et Sp pour avoir le test le plus significatif ?
Le gain diagnostique est important quand le RV+ est compris entre 5 et 10. Se et Sp doivent donc être grands.
II. En situation clinique.
Le médecin cherche surtout à ne pas "passer à côté d'une maladie" et
accepte " d'alerter à tord " un patient. Il abaisse le seuil de
positivité du test. Quelle est la conséquence :
a. Sur Se et Sp ?
Le choix d'un seuil bas augmente la sensibilité Se et diminue la spécificité Sp.
b. Sur le nombre dc de "faux positifs" ?
On augmente le nombre de faux positifs.
III. La courbe ROC.
Lors du dépistage de la trisomie 21, le test consiste à mesurer l'indicateur HCG.
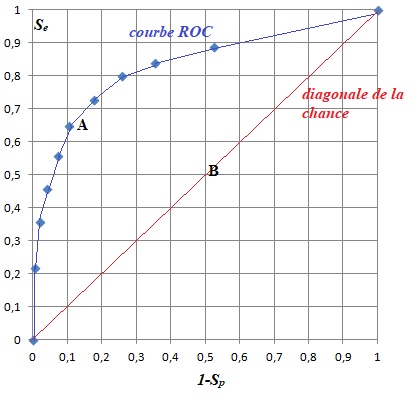
1. Pour un seuil de sensibilité 2 correspondant au point A.
a. Que vaut RV+ à 10-2 près.
RV+ = Se /(1-Sp) = 0,65 / 0,1025 =6,34.
b. Interpréter graphiquement cette valeur.
Le gain diagnostique est important quand le RV+ est compris entre 5 et 10. Se et Sp doivent donc être grands.
2. Pour le point B du graphique.
a. Que vaut RV+ ?
RV+ = Se /(1-Sp) = 0,5 / 0,5 = 1.
b. Que dire de ce test sérologique ?
Le gain diagnostique est faible.
Le patient a autant de chance d'être atteint de la maladie que d'en être indemne.
3. A quel point du graphique correspond le test parfait ?
Les tests peu performants se rapprochent de la diagonale.
Les tests bien discriminants se trouvent dans le coin supérieur gauche.
La sensibilité est égale à 1. La spécificité est égale à 1.
4. La capacité diagnostique d'un test peut être quantifiée par l'aire sous la courbe ROC.
a. Que vaut cette aire quand le test n'a pas d'intérêt ?
Aire située sous la diagonale rouge : 1 x1 / 2 = 0,5.
b. Que vaut cette aire quand le test est parfait ?
Aire du carré de côté 1 = 1.
c. Comment doit être cette aire pour que le test soit le meilleur possible ?
Cette aire doit être proche de 1. Plus l'aire sous la courbe est grande, meilleur est le test.
|
|