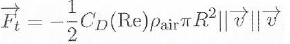Formation des nuages, chute d'une goutte d'eau, concours général 2021. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. .. .. . . .. .. ...... ... Un nuage se forme lorsqu'il y a liquéfaction de vapeur d'eau en altitude. Formation d'un nuage dans la basse atmosphère. L'air est constitué d'un mélange d'air sec et de vapeur d'eau. Tant qu'il n'y a pas liquéfaction, l'air sec et la vapeur d'eau peuvent être assimilés à des gaz parfaits. Soit nH2O la quantité de matière de vapeur d'eau contenue dans l'air. On appelle pression partielle de vapeur d'eau contenue dans l'air PH2O = nH2O RT /  V. On observe l'apparition de gouttes d'eau liquide dans l'air loorsqu'à une température fixée T la pression partielle d'eau est telle que : PH2O > Psat(T) où Psat (T) est la pression de vapeur saturante de l'eau. On note T0 = 298 K et P0 = 1,0 105 Pa, température et pression au niveau du sol. 13. L'évolution de la température en fonction de l'altitude z dans la basse atmosphère, appelée troposphère, est modélisée par une loi affine s'écrivant : T(z) = T0-lz avec l une constante. Estimer la valeur de l. 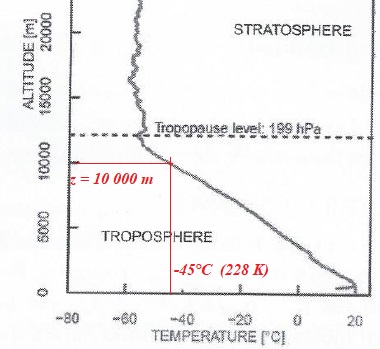l = (T0-T(z)) / z =(298-228) / 10 000 = 7 10-3 K m-1. Tant qu'il n'y a pas liquéfaction, l'air se comporte comme un gaz parfait et la pression totale P à l'intérieur d'un petit volume V d'air, qui s'élève dans la troposphère, suit une loi de la forme PVg = cste avec g = 1,4. 14. Montrer que la pression totale et la température à l'intérieur  d'un petit volume V d'air en ascension satisfont la relation  P(z)1-g T(z)g = cste. V = nRT(z) / P(z). P ( nRT(z) / P(z))g = cste  P(z)1-g T(z)g = cste / (nR)g =autre constante. 15. En déduire l'expression de P(z) en fonction de P0, T0, g et z.  P(z)1-g T(z)g = P01-g T0g . On pose ß = g /(1-g). P(z) = P0 (T0 /T(z))ß. P(z) = P0 (T0 / (T0-lz))ß. 16. On considère un air possédant une humidité relative P = mH2O / msec  =1 % où mH2O représente la masse de vapeur d'eau et msec la masse d'air sec. P étant très inférieur à 1, msec ~ mtot, masse totale de gaz. Montrer que la pression partielle de la vapeur d'eau dans l'air, à l'altitude z s'écrit : PH2O(z) = Msec / MH2O P P(z) MH2O = 18 g / mol et Msec = 29 g / mol. PH2O = nH2O RT /  V. Ptot =P(z) = ntot RT /  V. P(z) / PH2O = nair /  nH2O  ; PH2O =P(z) nH2O / ntot. nH2O / ntot = mH2O / MH2O  x Mtot / mtot  ~ mH2O / MH2O  x Msec / msec  ~P Msec / MH2O. PH2O(z) = Msec / MH2O P P(z). On se propose d'évaluer numériquement , à l'aide d'un programme Python, la vaelur de la pression partiele PH2O à différentes altitudes z. 1. z =[] # liste d'altitude (m). 2. T =[] # liste de température (K). 3. P =[] # liste de pression totale ( Pa). 4. PH2O =[] # liste de pression partielle  de vapeur ( Pa). 5. 6. for i in range (0,20): 7. z.append(500+i*100) 8. T.append(298-0.007*z[i]) 9. P.append(1.0e5*(298/(T[i])**(-1.4/0.4)) 10. PH2O.append((29/18)*0.01*P[i]) 17. Donner les valeurs : du premier élément, du pas en altitude et du dernier élément de la liste z. Combien d'éléments contient cette liste une fois la boucle "pour" terminée ? Première valeur de z : 500 +0*100 = 500 m ; pas en altitude : 100 ; dernière valeur de z : 500 +19 *100 = 2400. La liste compte 20 éléments. 18. Compléter la ligne 8 du programme afin de créer une liste T contenant les valeurs de température de l'air aux différentes altitudes contenues dans la liste z. T(z) = 298 -lz, donc : 8. T.append(298-0.007*z[i]) On a représenté les valeurs calculées de PH2O grâce au programme Python et la courbe Psat(T) en fonction de la température T de l'air. 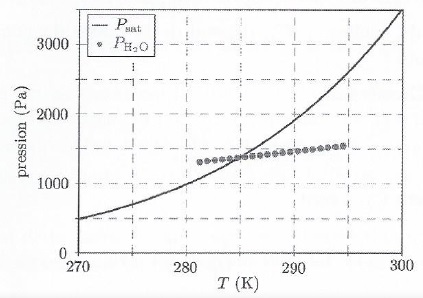19. Evaluer l'altitude de formation d'un nuage et commenter. Si PH2O > Psat, la liquéfaction débute. Le graphe indique T = 285 K. T(z) = T0-lz  ; z = (T0-T(z) / l =(298-285) / 0,007 ~1,9 103 m (1,9 km). 20. Pourquoi ce modèle n'est-il pas adapté pour décrire la formation de nuages dans la haute atmosphère ? La température n'évolue pas de manière linéaire dans la haute atmosphère. ... .... Chute d'une goutte d'eau. Un nuage s'est formé à l'altitude h = 1000 m. Une goutte sphérique de rayon R = 0,075 mm s'est formée dans la partie inférieure du nuage. Elle chute verticalement avec une vitesse initiale nulle. On note reau et rair les masses volumiques de l'eau et de l'air. L'étude est menée dans le référentiel du sol suivant un axe Oz vertical descendant. La goutte subit une foce de frottement 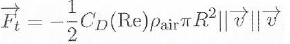Re =2R rair v / h, nombre de Reynolds, sans dimension, avec h = 1,8 10-5 S I. Pour Re < 1, CD =24 / Re ; pour 1 < Re < 5, CD =24 / Re +4,5. La poussée d'Archimède est négligée devant les autres forces appliquées sur la goutte. 21 . Par analyse dimensionnelle donner l'unité de h. R s'exprime en m ; rair s'exprime en kg m-3 ; v s'exprime en m s-1. h s'exprime en : m kg m-3 m s-1 soit kg m-1 s-1. On suppose que Re <1. 22. Etablir l'équation différentielle vérifiée par la composante verticale de la vitesse. Projeter la somme vectorielle des forces sur l'axe Oz : mg -12 / Re rair p R2 v2 = m dv /dt. dv / dt + 12 / Re rair p R2  / m v2 =g. Or Re =2R rair v / h. dv / dt + 12 / Re rair p R2  / m v2 =g. On pose t = m Re / (12 rair p R2 ) avec m = reau 4 / 3 p R3et Re = 2R rair v / h. t = 2 / 9 reauR2 / h. dv /dt + v / t = g. 23. En régime permanent, la goutte atteint une vitesse limite. Donner son expression et calculer sa valeur.   Lorsque le poids compense la force de frottement, la goutte atteint une vitesse limite. vlim = g t = g  2 / 9 reauR2 / h. vlim =9,8 x2 / 9 x1000 x(7,5 10-5)2 / (1,8 10-5) ~0,68 m /s. 24. Calculer la valeur du nombre de Reynolds en régime permanent et conclure. Re =2R rair v / h =2 x7,5 10-5 x1,3 x0,68 / (1,8 10-5) ~7,4. Cette valeur étant supérieure à1, l'hypothèse faite n'est pas valide. On suppose que 1 < Re < 5. 25. Montrer que la vitesse limite de la goutte est solution de l'équation : 3 rair R / (8h) v2lim +vlim -2greau R2 /(9 h) = 0. mg = 0,5 CD rair pR2 v2lim. 4 / 3 reau pR3 g=0,5 CD rair pR2 v2lim. 4 / 3 reau R g=0,5 rair CD  v2lim CD =24 / Re +4,5 ; Re =2R rair v / h ; CD =24 h /(2R rair vlim) +4,5. 4 / 3 reau R g=0,5 rair 24 h /(2R rair vlim) v2lim+4,5 *0,5 rair v2lim. 4 / 3 reau R g=6 h /R vlim+4,5 *0,5 rair v2lim. 4 / 3 reau R2 g=6 h  vlim+2,25 rair R v2lim. 2 / 9 reau R2 g / h = vlim+3 /8 rair R / h v2lim. 26. Calculer vlim puis Re. Conclure. 3 *1,3 *7,5 10-5 / (8*1,8 10-5)v2lim + vlim -2*9,8 *1000 *(7,5 10-5)2 /(9*1,8 10-5)=0. 2,03 v2lim + vlim -0,68 =0. Discriminant D =1+4*0,68*2,03 =6,52 =2,552. vlim = (-1+2,55) / 4,06 ~0,38 m /s. Re =2R rair v / h =2 x7,5 10-5 x1,3 x0,38 / (1,8 10-5) ~4,1. Hypothèse vérifiée. La courbe suivante représente la vitesse v en fonction du temps dans les premiers instants du mouvement de la goutte. 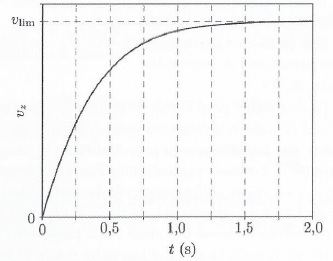27. Montrer que la distance parcourue par la goutte durant le régime transitoire est très petite devant celle parcourue durant le régime permanent. Conclure. Durée du régime transitoire : 1,5 s. Distance parcourue à la vitesse  v = 0,38 m /s durant 1,5 s : 0,38 x1,5 ~0,6 m. Cette valeur est négligeable devant h = 1000 m. 28. Calculer la durée de chute de la goutte. Commenter. h / vlim = 1000 / 0,38 =2,6 103 s~44 min. En 44 minutes, les vents et les flux d'air interviennent, accroissent la vitesse de la goutte, et la chute n'est pas verticale. 30. Justifier l'hypothèse selon laquelle la poussée d'Archimède peut être négligée devant les autres forces. Volume de la goutte : V = 4 / 3 pR3 = 4 /3 x3,14 x(7,5 10-5)3 ~1,8 10-12 m3. Poids : reau V g =1000 x1,8 10-12 x9,8 ~1,7 10-8 N Poussée : rair V g =1,3 x1,8 10-12 x9,8 ~2,3 10-11 N. La masse volumique de l'air étant environ 1000 fois plus faible que la masse volumique de l'eau, la poussée d'Archimède due à l'air est négligeable devant le poids. Force de frottement en régime permanent : Re =4,1 ; CD =24 / Re +4,5 =24 /4,1 +4,5 ~10.  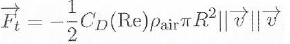F =0,5  x10 x1,3 x3,14 x(7,5 10-5)2 x0,382 ~1,7 10-8 N. La poussée d'Archimède due à l'air est négligeable devant les frottements durant le régime permanent.. Nuage et coup de foudre. Les cumulonimbus sont de gros nuages en forme d'enclume. Leur base se situe à environ 1 km d'altitude ; leur sommet à plus de 10 km. Ils sont constitués de gouttes d'eau à leur base et de grêlons au sommet. Lors d'un orage, ces nuages sont parcourus de forts courants de convection ascendant et descendant provoquant des collisions entre particules de glace et  de gouttes d'eau. Des charges électriques apparaissent. Les grêlons du sommet se chargent positivement et les gouttes d'eau de la base se chargent négativement. La surface de la terre se charge positivement par influence. La surface terreste et la base du nuage se comportent comme un condensateur plan de capacité C = e0A / d avec e0 = 8,85 10-12 F. A : aire de la base du nuage et d l'altitude du nuage. La tension entre les armatures de ce condensateur peut atteindre 20 MV. Cette haute tension reste insuffisante pour ioniser l'air entre la terre et la base du nuage. Le coup de foudre est initié par l'émission de traceurs ( particules chargées)  qui s'échappent de la base du nuage. Accélérés par la différence de potentiel entre nuage et sol, ces traceurs progressent à une vitesse de l'ordre de 200 km /s et ionisent par collision, l'air sur leur passage : il en résulte un canal conducteur. Lorsqu'un traceur s'approche suffisamment du sol, la tension entre le traceur et le sol, est telle qu'une décharge ascendante se produit. Le canal conducteur formé relie directement le sol au nuage : une puissante décharge sur une durée de 500 µs se produit. C'est le coup de foudre qui engendre éclair et tonnerre.  Evaluer l'ordre de grandeur de l'intensité du courant circulant lors d'un coup de foudre. Discuter de l'intérêt de mettre en place un dispositif de récupération de cette énergie. 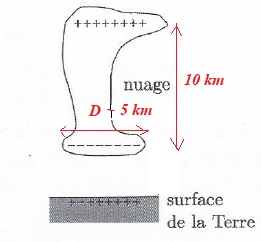Aire de la base circulaire du nuage : A = p R2 avec R ~ 2,5 km ; A = 3,14 x(2,5 103)2 =1,96 107 m2. Capacité du condensateur : C = e0A / d = 8,85 10-12 x1,96 107 / 1000 =1,74 10-7 F. Charge perdue lors du coup de foudre : q = C U = 1,74 10-7 x 20 106 =3,48 C. Durée de la décharge : 500 µs. Intensité correspondante : I =  q / Dt =3,48 / (500 10-6) ~ 7 103 A. Energie correspondante : U I Dt = 20 106 x7 103 x500 10-6 ~7 107 J. Il n'y a aucune technologie permettant actuellement de récupérer une telle énergie de  produite en 500 µs.

menu