Physique chimie, positionnement d'un navire par GPS, concours général 2020. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. .. .. . . .. .. ...... ... Le principe du positionnement GPS repose sur la mesure de la distance entre le récepteur GPS et plusieurs satellites émetteurs. La distance est calculée à partir du temps mis par un signal porté par une onde électromagnétique pour parcourir cette distance. La position de chaque satellite dans l'espace et l'heure exacte de transmission du message sont connues avec une grande précision par le récepteur. 1. les satellites constituant le système GPS émettent leurs signaux à des fréquences f1 et f2, ayant pour valeurs respectives f1 = 1575,42 MHz et f2 = 1227,60 MHz. Citer le domaine du spectre électromagnétique dans lequel se situent ces deux fréquences.  Calculer les longueurs d'onde dans le vide correspondantes. Les satellites du système GPS émettent des signaux codés sous forme d'ondes radio émises. l = c / f avec f : fréquence en Hz ; c, célérité en m/s, l : longueur d'onde en m. Pour f = 1,57542 109 Hz : l1 = 3,00 108 / (1,57542 109 )=0,1904 m soit l1 = 0,190 m. Pour f = 1,2276 109 Hz : l2 = 3,00 108 / (1,2276 109 )= 0,244 m. 2. P Correia écrit : " Lle principal problème consiste à mesurer le délai avec une grande précision, lorsqu'on sait qu'une erreur d'un millionième de seconde provoque une erreur de 300 m sur la position". Commenter de manière raisonnée cette affirmation. Erreur sur la position : c Dt =3,00108 x 1,010-6 = 300 m. 3. Les satellites sont situés sur une orbite quasi-circulaire à une altitude de 20200 km. La période de révolution est de 11 h 58 min 2 s. Calculer la vitesse moyenne du satellite sur cette orbite. Circonférence : 2 p (Rterre +altitude) =2 *3,14 ( 6400 +20200)=1,67 105 km. Période de révolution : 11 *3600 +58 *60 +2 = 4,3082 104 s. Vitesse moyenne : 1,67 105 / (4,3082 104 )=3,876 ~3,9 km / s. L'horloge embarquée dans le satellite subit les effets de la relativité restreinte et en particulier la dilatation des temps. Les horloges atomiques des satellites, en mouvement à grande vitesse autour de la terre, battent plus lentement que celles restées immobiles au sol. A partir du lancement du satellite, un décalage s'installe au fil des jours entre le temps Tréf mesiuré à bord du satellite et le temps T0 mesuré sur terre : les horloges placées au sol et dans le satellite se désynchronisent. On appelle DTréf la correction relativiste à apporter sur le temps de parcours du signal entre le satellite et le récepteur à la surface de la terre et T0 le temps écoulé depuis la synchronisation entre l'horloge placée dans le satellite et  celle restée au niveau du sol. DTréf = 0,5 v2 T0 / c2. 4. Le premier satellite a été lancé le 23 / 12 /2018. les horloges sont synchronisées au moment du lancement. On repère la position d'un objet placé à la surface de la terre par GPS à la date du 11 / 3 / 2020. Calculer la correction relativiste à apporter sur le temps de parcours du signal entre le satellite et le récepteur terrestre et estimer s'il y a lieu de tenir compte de cette correction. T0 ~453 jours soit environ 3,9 107 s. DTréf = 0,5 (3,9103)2 *3,9 107 / (3,00 108)2~3,3 10-3 s. Une erreur d'un millionième de seconde provoque une erreur de 300 m sur la position". Il faut prendre en compte la correction relativiste. ... .... 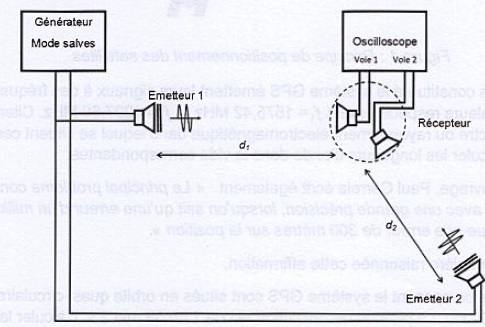Expérience de modèlisation de GPS. Des élèves souhaitent construire une maquette simplifiée de GPS. Ils utilisent  deux émetteurs ultrasonores ( représentant les satellites ) et deux récepteurs ultrasonores fixés sur l'objet dont on veut repérer la position. Ces deux récepteurs sont reliés à un système d'acquisition. les deux récepteurs modèlisent le récepteur GPS. Les deux émetteurs sont alimentés par le même générateur de salves et envoient au même instant t0 une impulsion ultrasonore de durée 5 ms en direction des récepteurs. L'atgténuation est négligeable sur la distance parcourue. La vitesse de propagation des ondes est c=340 m /s. 5. Donner la gamme de fréquences des ondes ultrasonres. Décrire leur nature. Ce sont des ondes mécaniques longitudinales dont les fréquences vont de 20 kHz à 10 MHz. 6. Estimer le nombre de périodes constituant la salve émise. Pour une fréquence f = 20 kHz = 2,0 104 Hz ; période T = 1 /(2,0 104) =5 10-5 s = 0,05 ms. Nombre de périodes par salves : 5 / 0,05 = 100. Les récepteurs sont constitués d'un capteur et d'un conformateur électronique qui délivrent un signal binaire : - 1 V en absence de réception et +1 V en présence d'une onde reçue. 7. Les signaux suivants sont observés sur l'oscilloscope. La date t0 = 0 correspond à l'émission simultanée du signal par les deux émetteurs. Montrer que la distance entre l'émetteur 1 et le récepteur est d1 = c (t1-t0). En déduire l'expression de d2. Les calculer. 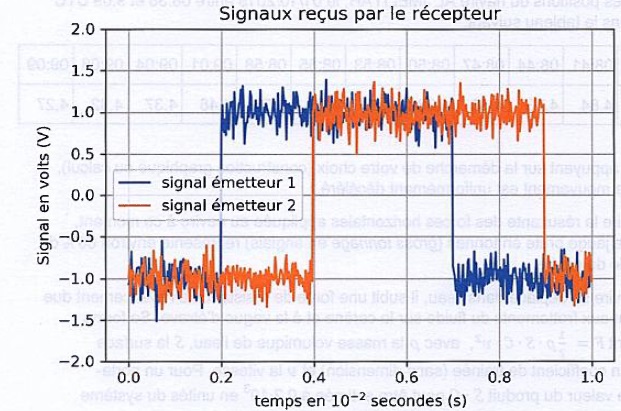Durée du parcours d1 : retard du signal reçu = t1-t0 =0,2 10-2 = 2 10-3 s. Célérité des ondes : c = 340 m /s. d1 = 340 * 2 10-3 =0,68 m. Durée du parcours d2 :retard du signal reçu = t2-t0 =0,4 10-2 = 4 10-3 s. d2 = 340 * 4 10-3 =1,36 m. 8. Représenter l'ensemble des positions compatibles avec d1 et d2. Déterminer la position du récepteur. Expliquer quelle modifications il faudrait apporter à la maquette pour déterminer, parmi les positions possibles, celle du récepteur. 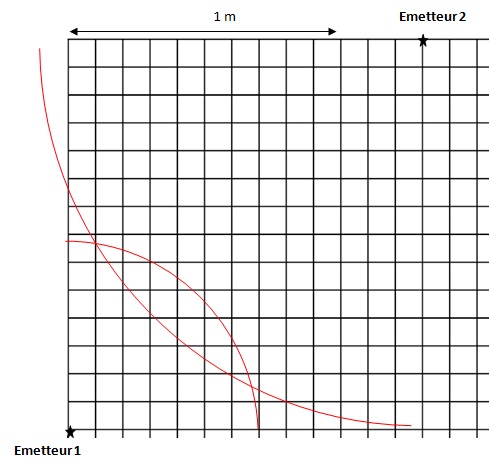Deux positions du récepteur sont possibles. 9. En généralisant à trois dimensions, déterminer le nombre minimum de satellites permettant de déterminer la position d'un récepteur GPS. 10. Expliquer l'intérêt d'avoir un nombre de satellites plus grand que le minimum nécessaire. Le principe d'une mesure est le suivant : un utilisateur détermine sa distance à un premier satellite. Il peut alors affirmer qu'il se trouve sur la surface d'une sphère de rayon égal à cette distance et centrée sur ce satellite. L'utilisateur détermine ensuite sa distance à un deuxième satellite, ce qui lui permet de déduire qu'il se trouve à l'intersection de deux sphères, c'est à dire sur un cercle. Enfin , la détermination de sa distance à un troisième satellite place l'utilisateur sur une troisième sphère, ce qui réduit ses positions possibles à deux points, l'utilisateur peut soit effectuer une quatrième mesure, soit rejeter le point dont l'altitude est aberrante. Pour la science n°320, juin 2004. .

menu