Physique,
concours Puissance alpha 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Exercice 1.
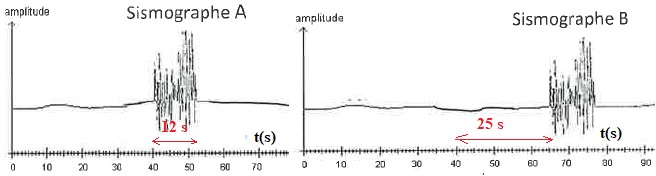
Deux sismographes A et B, distants de d = 150 km enregistrent la même
secousse lors d'un séisme. On considère que la vitesse de l'onde
sismique reste constante.
a. L'onde sismique transfert une quantité d'énergie et de matière. Faux.
L'onde sismique transfert une quantité d'énergie.
b. La durée de la secousse a été de 25 s. Faux ( 12 s).
c. La vitesse de propagation de cette onde est de 6,0 km / h. Faux.
150 km parcouru en 25 s ; 150 /25 =6,0 km / s ou 6 x3600 =21,6 103 km / h.
Un troisième sismographe perçoit le front d'onde sismique à la date t = 77,5 s.
d. Il se situe à 225 km du sismographe A. Vrai.
77,5 -40 = 37,5 s.
37,5 x 6,0 =225 km.
Exercice 2. Puissance et intensité acoustiques.
Une source sonore S que l'on considère comme ponctuelle et isotrope,
émet un son depuis un point O. La mesure du niveau d'intensité sonore
du son produit, en un point M situé à la distance OM =10 m de la
source, est de 70 dB.
Pour une source isotrope de puissance P(W), l'intensité acoustique I en
un point M distant de D(m) de la source est : I = P /(4pD2).
a. Le niveau d'intensité sonore L se calcule par la relation : L = 10 log ( I / I0). Vrai.
b. L'intensité acoustique de référence I0 correspond au seuil de la douleur pour l'oreille humaine. Faux.
I0 correspond au seuil de sensibilité de l'oreille humaine.
c. La puissance acoustique P est d'environ 12,6 mW. Vrai.
I = I0 x10L / 10 = 10-12 x 107 = 10-5 W m-2.
P = 4pD2I = 4 x3,14 x102 x10-5 =12,6 10-3 W = 12,6 mW.
d. En doublant la distance D, l'intensité acoustique est divisée par 2. Faux ( divisé par 22=4).
Exercice 3. Propriétés des ondes.
Afin de vérifier la valeur du diamètre d'un fil de suture, on effectue
l'expérience suivante à l'aide d'un faisceau laser rouge de longueur
d'onde l = 630 nm. On donne L = 20 mm.
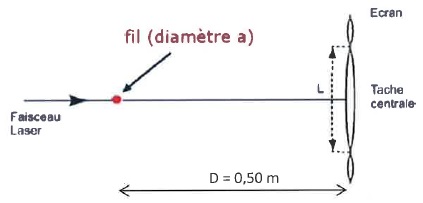
L = 20 mm.
a. Il s'agit d'une expérience d'interférences lumineuses par un fil. Faux. ( diffraction par un fil ).
b. Le diamètre du fil est environ 31 µm. Vrai.
a = 2 l D / L =2 x 0,630 x0,50 /0,020 =31,5 µm.
c. La même expérience réalisée avec un laser de couleur bleue aurait donné une tache centrale moins large. Vrai.
L = 2 l D / a ; les longueurs d'onde du bleu sont inférieures à celles du rouge.
d. Si l'on remplaçait le fil par une fente de largeur a = 10,0 mm, on observerait le même type de figure sur l'écran. Faux.
La largeur de la fente est beaucoup trop grande, très supérieure à la longueur d'onde de la lumière.
Exercice 4. Déplacement d'un hélicoptère.
Un observateur immobile perçoit des bips sonores de période d'émission T0 = 1,25 ms émis par un hélicoptère A se trouvant à l'altitude h au dessus du sol. Ce signal se propage à la célérité Vson par rapport au référentiel terrestre.
Lorsque l'hélicoptère se déplace en direction de l'observateur à une vitesse constante VS, l'observateur perçoit alors les différents bips séparés d'une durée T ' = T0 (1-VS / Vson).
On donne 6,25 x 3,2 = 20.
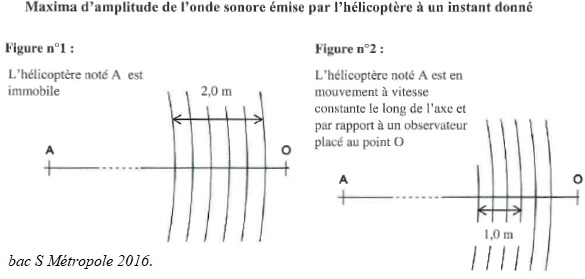
a. La célérité du son dans l'air à l'altitude h est 320 m /s. Vrai.
l = 2,0 / 5 = 0,40 m ; c = l / T0 = 0,40 / (1,25 10-3) =320 m /s.
b. La longueur
d'onde de l'onde sonore, lorsque l'hélicoptère est immobile, est le
double de celle quand il est en mouvement. Faux.
Immobile : l = 0,40 m ; en mouvement l = 1,0 /3 = 0,33 m.
c. Lors du déplacement de l'hélicoptère, le son perçu par l'observateur est plus grave. Faux.
T ' = T0 (1-VS / Vson) ; T ' < T0 ; f ' > f0, son plus aigu.
d. L'hélicoptère se déplace à une vitesse proche de 192 km / h. Vrai.
l / l0 = T ' / T0 = (1 / 3) / 0,4 =1 / 1,2.
1-VS / Vson = 1 / 1,2 ; VS / Vson =1-1 /1,2 =0,2 / 1,2 = 1 / 6.
VS = Vson / 6 = 320 / 6 m /s soit 320 / 6 x3,6 =320 x0,6 =192 km / h.
Exercice 5. Le pénalty.
Le joueur dépose le ballon au point de pénalty O, pris comme origine du
repère, puis tape celui-ci en direction du centre du but en lui
communiquant une vitesse initiale v0 = 20,0 m /s dont la direction fait un angle a = 45 ° par rapport à l'horizontale.
A est le point où se situe le ballon en franchissant la ligne de but.
Equations horaires de la vitesse du centre d'inertie du ballon :
vx(t) = V0 cos a ; vz(t) = -gt +V0 sina.
On néglige les frottements et la poussée d'Archimède.
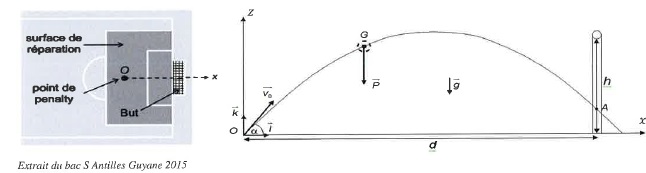
h = 2,4 m ; d = 11,0 m ; g = 10 m s-2 ; 2½~1,4 ; 1,21 x25 = 30.
a. L'équation de la trajectoire du ballon est z(x) = -25 10-3 x2 +x. Vrai.
x(t) = V0 cos a t ; z(t) =-½gt2 +V0 sina t.
t = x / ( V0 cos a) ; z(x)= -0,5x2 /( V0 cos a)2+ x tan a .
( V0 cos a)2 = (20 *2½ /2)2 =200 ; -0,5*10 / 200 = -25 10-3 ; tan 45 = 1.
b. Le ballon atteint le sommet de la trajectoire en moins d'une seconde. Faux.
Au sommet, la composante verticale de la vitesse est nulle.
-10t +20 sin 45 =0 ; t = 2 sin 45 ~ 1,4 s.
c. Le pénalty est réussi. Faux.
z(11) = -25 10-3 112 +11=25 *0,121+11 =3+11=14 m, valeur supérieure à h.
d. Le ballon franchi la ligne de but avec une vitesse inférieure à V0. Vrai.
t = x / ( V0 cos a) = 11 /( 20 cos 45) =11 /(20*1,4) = 11 / 28.
vx(t) ~ 20 *0,7 ~1,4 ; vz(t) = -10 t +20 *0,7 = -11 /2,8 +14= -1,4 +14 = 12,6.
V =[1,42 +12,62]½ =12,7 m /s.
Exercice 6. Particule chargée dans un champ électrique.
On étudie le mouvement d'un ion lithium Li+ de masse m =1,0 10-26
kg émis par un canon à particules. Cet ion pénètre en un point O, dans
l'espace situé entre 2 plaques horizontales de longueur L = 10 cm et de
charges opposées, avec une vitesse initiale V0 = 4,0 104 m /s.
Intensité du champ électrique entre les plaques : E =1,5 kV / m.
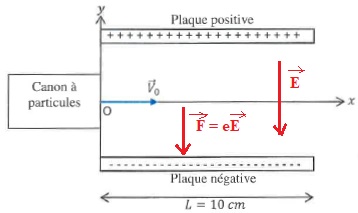
a. L'ion est dévié vers le haut. Faux.
L'équation de la trajectoire d'un ion lithium est y = -eE /(2mv02) x2.
b. La déviation ( distance parcourue verticalement )par l'ion Li+est proportionnelle à la distance horizontale parcourue entre les plaques. Faux. ( y = constante fois x2).
c. A la sortie des plaques, l'ion aura dévié de 7,5 cm par rapport à l'horizontale. Vrai.
eE /(2mv02) =1,6 10-19 *1500 / (2 10-26*1,6 109) =1,5 /2 10-16 / 10-17=7,5.
y = -7,5 x2 = -7,5 *0,102 =-7,5 10-2 m = -7,5 cm.
d. Si la largeur des plaques avait été L = 5,0 cm, la déviation aurait été deux fois moins importante. Faux.
y = -7,5 x2 = -7,5 *0,052 =-1,875 10-2 m = -1,87 cm.
|
|
|
....
|
Exercice 7. Les satellites de Jupiter.
Jupiter possède 69 satellites naturels.Ces satellites suivent la troisième loi de Kepler T2 / r3 = 4p2 / ( GMJ). La période de révolution de Ganymède est TG = 7,1 jours terrestre soit environ 6 105 s.
MJ = 2 1027 kg ; G = 7 10-11 SI ; p ~3.
Racine cubique (1,4) ~ 1 ; racine carrée (1,4) ~1,2.
a.
La masse de Ganymède étant inférieure à la masse de Jupiter, la force
exercée par Ganymède sur Jupiter est inférieure à la force exercée pat
Jupiter sur Ganymède. Faux.
b. Plus le satellite est proche de Jupiter, plus sa période de révolution augmente. Faux.
T2 / r3 =constante ; si r diminue, alors T diminue.
c. Le rayon de l'orbite de Ganymède est d'environ 1 x 106 km. Vrai.
4p2 / ( GMJ) ~4 x 9 /(7 10-11 x 2 1027) = 18 / (7 1016).
r3 = T2 / 18 * (7 1016)=36 1010 *7 1016 / 18 =2 * 7 1026 = 1,4 1027 ; r ~ 109 m = 1 x 106 km.
d. Un satellite
évoluant sur une orbite dont le rayon est 4 fois plus grand que celui
de Ganymède, mettre 8 fois plus de temps que Ganymède pour
effectuer un tour sur son orbite. Vrai.
T2 / r3 =constante ; T2 / r3 = T ' 2 / (64 r3 ) ; T2 T ' 2 / 64 ;T = T' / 8 ; T ' = 8 T.
si r est multiplié par 4, alors T est multiplié par 8.
Exercice 8. Fête foraine.
La personne qui teste sa force pousse un chariot initialement immobile de masse m = 4,00 kg sur une longueur OA = l = 0,80 m. Force horizontale de valeur supposée constante F = 250 N.
En A le chariot aborde une partie circulaire AB pour venir frapper
éventuellemnt la cible située en B. Entre A et B le centre d'inertie du
chariot s'élève d'une hauteur h = 2,50 m.
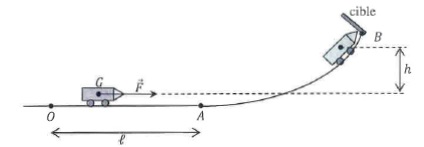
On néglige les frottements.
L'attraction affiche "Faible " si le chariot frappe la cible avec une vitesse inférieure à 3,0 m /s.
L'attraction affiche "Fort " si le chariot frappe la cible avec une vitesse comprise entre à 3,0 m /s et 5,0 m /s.
L'attraction affiche "Très fort " si le chariot frappe la cible avec une vitesse supérieure à 5,0 m /s.
a. Entre O et A, le chariot n'est soumis qu'à deux forces, son poids et la force de poussée F. Faux.
Il faut ajouter l'action du support, perpendiculaire au plan et opposée au poids.
b. La vitesse du chariot en A est vA = 10,0 m /s. Vrai.
Seule la force F travaille entre O et A( poids et action du plan, perpendiculaire au déplacement, ne travaillent pas ).
Travail de F : W = F OA = 250 x0,8 = 200 J.
Variation de l'énergie cinétique du chariot : ½mvA2 -0 = 200 ; v2A = 400 / 4 = 100 ; vA = 10 m /s.
c. Entre A et B, le travail du poids a pour expression W = mgh. Faux.
En montée, le travail du poids est résistant et vaut W = -mgh.
d. L'attraction va indiquer "Fort". Faux.
Travail des forces entre A et B : -mgh = -4 x10 x2,5 = -100 J.
Théorème de l'énergie cinétique entre A et B : ½mvB2 -½mvA2 = -100 ;
½mvB2 -200 = -100 ; ½mvB2 = 100 ; vB2 = 100 x2 / 4,0 = 50 ; vB ~7 m /s. ( " Trés Fort").
Exercice 9. Le matelas du randonneur.
Température de la peau : 33°C.
Température de l'air et du sol : 13°C
Le matelas est assimilé à une paroi plane.
a. Au niveau macroscopique le transfert thermique s'effectue du randonneur vers le sol. Faux.
Transfert thermique du matelas vers le sol.
b. Au niveau microscopique le transfert thermique est un transfert par conduction. Vrai.
c. Le transfert thermique à travers le matelas "Rando" est de 60 kW. Faux.
Conductivité thermique l = 30 mW K-1 m-1 ; épaisseur e = 1,0 cm ; surface S =2,0 x0,50 = 1,0 m2.
Résistance thermique Rth = e / (lS) = 0,010 / (0,030 x1,0) = 1 / 3 K W-1.
Flux thermique : DT / >Rth = (33-13) x 3 = 60 W.
Avec un matelas "Excurso" on mesure une énergie thermique de 2,16 104 J pendant une heure.
d. Son épaisseur est de 3,0 cm. Faux.
Flux thermique : 2,16 104 / 3600 = 6,0 J.
Rth = 20 / 6,0 = 10 / 3 K W-1.
Conductivité thermique l = 60 mW K-1 m-1 ; surface S =2,0 x0,50 = 1,0 m2.
e = Rth l S =10 / 3 x 0,060 =0,2 m = 20 cm.
Exercice 10. Le traitement de la cornée au laser.
Fréquence moyenne du rayonnement : F = 3,0 102 THz. T = 1012.
Fréquence des impulsions : f = 10 kHz.
Durée d'une impulsion : 500 fs. (f = 10-15)
Energie transportée par impulsion : E = 0,10 µJ.
a. Ce laser émet dans le rouge. Faux.
l = c / F = 3,0 108 /(3,0 1014) =1,0 10-6 m = 1,0 µm ( proche IR).
b. Dans ce laser, la lumière est produite par émission stimulée. Vrai.
c. La puissance d'une impulsion est de 2,0 MW. Faux.
énergie (J) / durée (s) =1,0 10-7 / (5,00 10-13) =2,0 105 W = 0,2 MW.
d. Il y a environ 500 milliards de photons émis au cours d'une impulsion. Vrai.
Energie d'un photon : h F =6,6 10-34 x 3,0 1014 ~2 10-19 J.
1,0 10-7 / (2 10-19) ~5,0 1011 = 500 milliards.
Exercice 11. Fentes de Young.
Une assemblée d'atomes de Néon est immobilisée à une hauteur L = 50 mm
au dessus de deux fentes distantes de d = 6 µm. On laisse tomber un
nuage d'atomes, en chute libre sans vitesse initiale, à intervalle de
temps réguliers. Un écran de détection est placé en contrebas pour
recevoir les atomes dont les impacts sont matérialisés en points noirs.
La distance entre la double fente et l'écran est D = 120 mm. On a
représenté l'écran de détection à deux instants différents.
Masse d'un atome de néon : m = 3,3 10-26 kg.
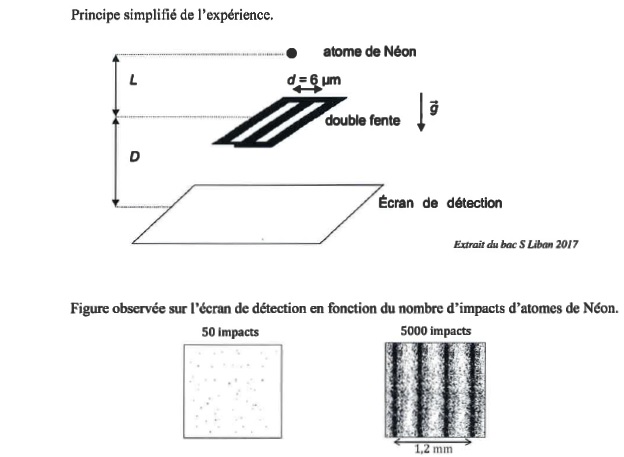
a. Il est possible de prévoir la position d'impact d'un atome de néon. Faux.
b. Cette expérience met en évidence le caractère ondulatoire de la matière. Vrai.
Les interférences mettent en évidence le caractère ondulatoire de la matière.
c. Les atomes atteignent la double fente avec une vitesse proche de celle de la lumière. Faux.
L'atome n'est soumis qu'à son poids, vertical vers le bas, valeur mg.
Sa chute est libre suivant la verticale descendante. Le vecteur vitesse est tangent à la trajectoire verticale.
Variation de l'énergie cinétique de l'atome entre l'instant de départ et la double fente : ½mv2 -0.
Travail moteur du poids : mg L.
Le théorème de l'énergie cinétique conduit à : ½mv2 = mgL ; v =(2gL)½ = (2x10 x0,050)½=1 m /s.
d. Au niveau de la double fennte, la longueur d'onde associée à un atome de néon est de 20 nm. Vrai.
l = h /(m v)=6,6 10-34 / (3,3 10-26 x1) = 2 10-8 m = 20 nm.
Exercice 12. Transmission des images.
La réception des images TV peut se faire à l'aide d'une antenne
parabolique ou en passant par une fibre optique. Dans les 2 cas le
signal subit un affaiblissement : la puissance de sortie Ps ( en W) est inférieure à la puissance d'entrée Pe ( en W).
On définit son atténuation A = 10 log ( Pe /Ps) ( en dB).
Le signal reçu par l'antenne est transféré par un câble coaxial de 25 m jusqu'au récepteur.
Atténuation du câble A = 20 dB pour 100 m. Débit binaire : D = 100 Mbits / s.
Fibre optique : A = 0,2 dB pour 1 km ; D = 1 Gbits / s.
On prendra 10½~ 3.
a. Le signal transmis par le câble est un signal analogique. Faux.
Signal numérique.
b. La puissance de sortie du câble sera 4 fois plus faible que la puissance fournie par la parabole à l'entrée du câble.
A = 5 dB ; 5 = 10 log( Pe /Ps) ; log( Pe /Ps) = 0,5 ; Pe /Ps = 100.5 ~3.
On remplace ce câble par une fibre optique.
c. la transmission par fibre optique utilise le phénomène de réfraction. Faux.
Réflexion totale.
d. La transmission d'un fichier de 5 Mo par cette fibre prendra 40 ms. Vrai.
D = 1000 Mbits / s = 1000 /8 =125 Mo /s.
5 /125 =1 / 25 = 0,040 s = 40 ms.
|
|