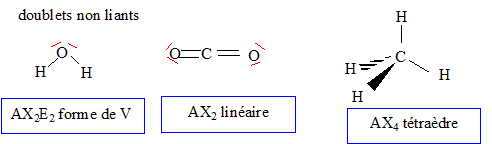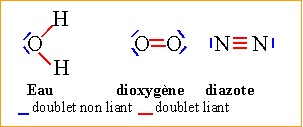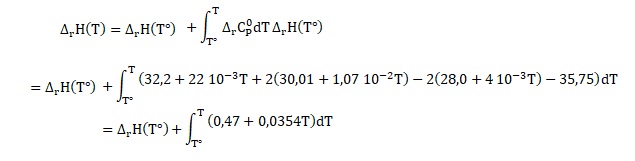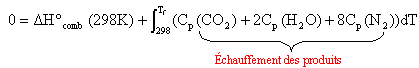Chimie,
Concours interne IIM 2021.
Combustion du méthane, équilibre chimique, pH d'une solution aqueuse.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Combustion du méthane.
1.
Rappeler les schémas de Lewis des atomes de carbone, d'hydrogène,
oxygène et azote. Donner les formules développées du méthane, dioxygène
et diazote. Quels sont les configurations électroniques des atomes H,
C, N et O. A quelle famille chimique appartient le méthane ?
Les configurations
électroniques des atomes H, C, N et O :
H : 1s1 ; C :
1s2 2s2 2p2 ; O :
1s2 2s2 2p4 ; N :
1s2 2s2 2p3 .
Formules de Lewis pour les
molécules d'eau, de dioxyde de carbone et de
méthane :
La géométrie de ces
trois molécules dans le cadre de la méthode
VSEPR
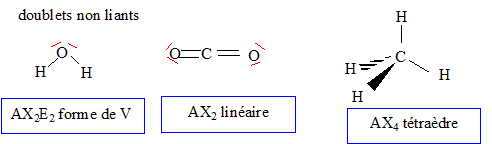
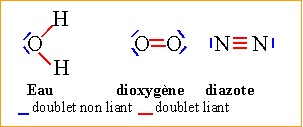
Le méthane appartient à la famille des alcanes.
La combustion du méthane produit du dioxyde de carbone et de l'eau.
2. Donner les formules de Lewis du dioxyde de carbone et de l'eau.
3. Equilibrer l'équation de combustion du méthane.
CH4(g) + 2
O2(g) = CO2(g) + 2H2O(liq)
4. Calculer l'enthalpie de cette réaction.
DrH°1
= DfH°(CO2)
+ 2DfH°(H2O)
- 2DfH°(O2)
- DfH°(CH4)
DrH°1
=-393,5 + 2*(-241,8) -(-74,4) =
-802,7 kJ
mol-1.
5. On se propose de faire la combustion de 1 Nm3 de méthane. ( volume de gaz mesuré dans les conditions normales de température et de pression (273 K et 1,013 bar).
a. De quelle quantité d'oxygène a t-on besoin ?
Quantité de matière de méthane n = PV / (RT) =1,013 105 x 1 /(8,314 x273) =44,6 mol.
Quantité de matière de dioxygène : 2n = 2 x44,6 = 89,2 mol.
b. Quelles quantités de CO2 et d'H2O produit-on ?
n(CO2) = 44,6 mol ; n(H2O) = 89,2 mol.
c. Si la combustion est réalisée à l'air, quel est le volume de gaz produit en Nm3 ? On suppose l'eau sous forme de vapeur.
Volume CO2 : 44,6 x 22,4 ~999 L ~1 Nm3.
Volume H2O : 89,2 x 22,4 ~1998 L ~2 Nm3.
Volume de O2 : 2 Nm3.
Volume de diazote = 4 volume O2 = 8 Nm3.
Total : 1 +2 +8 =11 Nm3.
5. Déterminer l'enthalpie de réaction en fonction des capacités calorifiques.
DrH°1
= DfH°(CO2)
+ 2DfH°(H2O)
- 2DfH°(O2)
- DfH°(CH4)
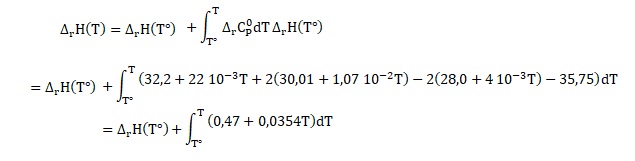
6. On
suppose que la combustion à l'air est réalisée dans un réacteur
adiabatique à pression constante. Quelle est la valeur de la
température finale atteinte ?
L'air
contient en mol 20% de dioxygène et 80% de diazote
:
CH4(g)
+ 2O2 (g) + 8N2(g) -->
CO2 (g) + 2H2O (g) +
8N2(g)
On applique
la loi de Kirchhoff à un système adiabatique (
pas de transfert de chaleur vers l'extérieur) :
La chaleur
libérée par la combustion sert à
chauffer les produits de la réaction .
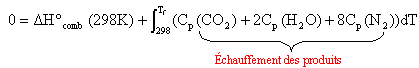
Total
capacité calorifique: 0,47 + 0,0354 T +8(27,88 +4,27 10-3 T) =223,51 +0,06956 T. ( J / mol).
Intégrer entre 298 K et Tfinale= T.
223,51 T +0,03478 T2 -223,51 x298 -0,03478 x2982 =223,51 T +0,03478 T2 -6,97 104.
-8,027 105 +223,51 T +0,03478 T2 -6,97 104 = 0
0,03478 T2+223,51 T-8,72 105 = 0.
Discriminant = 223,512 +4x0,03478 x8,72 105 =1,71 105 =(414)2.
Solution positive retenue : (-223,51 +414) / (2x0,03478)~2736 K.
7. Le débit de méthane du brûleur vaut 5 Nm3 h-1.
La combustion est réalisée à une température proche de 1200 °C.
Pourquoi cette température est-elle très différente de la température
de flamme ? Quelle est la valeur du flux thermique en watts ?
L"énergie de la combustion sert également à chauffer le milieu extérieur ( système non adiabatique).
Flux thermique =| énergie de la combustion de 5 Nm3 | / durée en seconde.
5 x 8,027 105/ 3600 =1,11 103 W / mol.
8. La
capacité calorifique de l'eau est 4,15 kJ kg-1 K-1. Le débit volumique
de l'eau est de 50 L / min. Quelle est l'élévation de la température de
l'eau ?
50 L / min = 50 / 60 kg /s = 0,833 kg / s.
Energie reçue par l'eau en une seconde =44,6 x 5 x1,11 103 J
DT = 44,6 x5 x1,11 103 /(0,833 x4,15 103) =71,6 °C.
Equilibres chimiques.
Lors de la combustion du méthane, le diazote peut s'oxyder en N2O4. Ce dernier peut se dissocier en NO2. La réaction inverse est la dimérisation de NO2.
1) Donner le schéma de lewis de NO2 et N2O4.
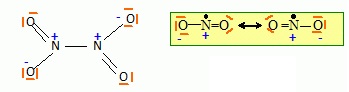
2. Calculer l'enthalpie de la réaction de dimérisation. Conclure.
2NO2 --> N2O4.
DrH° = DfH° (N2O4)-2 DfH° (NO2) =9,2-2*33,8 = -58,4 kJ mol-1, valeur négative donc exothermique.
3. Compléter le tableau d'avancement suivant suivant, x étant la fraction de dissociation. Montrer que Kp = 4x2 / (1-x2) P.
|
avancement
|
N2O4
|
---> 2NO2
|
t=0
|
0
|
1
|
0
|
t
|
x
|
1-x
|
2x
|
fraction molaire
|
|
(1-x) / (1+x) |
2x /(1+x)
|
Pression partielle P(N2O4 ) = (1-x) P/ (1+x).
Pression partielle P(NO2 ) = 2x P/ (1+x).
KP =P2(NO2 ) / P(N2O4 ) = 4x2 / (1-x2) P.
4. Montrer que dln(KP)/dT = DrH/(RT2).
DrG° = DrH - T DrS= -RT ln KP.
ln KP = -DrH /(RT) + DrS / R.
Si DrH et DrS ne dépendent pas de la température :
dln(KP)/dT = DrH/(RT2). Relation de Van' t Hoff.
5. Proposer une méthode permettant de déterminer l'enthalpie de réaction en fonction de la température.
Pour différentes températures T, déterminer x.
Calculer KP.
Utiliser la relation de Van' t Hoff.

6. L'expression de la constante d'équilibre en fonction de la température s'écrit :
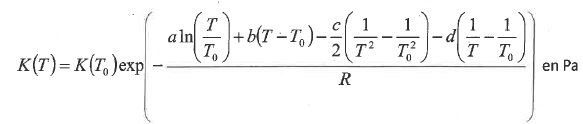
a = -1,965 J mol-1 K-1 ; b = 0,011328 J mol-2 K-2 : c = 142210 J mol-1 K ; d = -59297,9 J mol-1.
La valeur de la constante thermodynamique d'équilibre e la réaction à 25°C est de 14800 Pa.( 0,1458 bar)
Compléter
les tableaux suivants et conclure sur l'influence de la
température et de la pression sur la réaction de dissociation.
T( K)
|
x expérimental
|
x calculé
|
299,85
|
0,1995
|
0,1997
|
312,95
|
0,2923
|
0,31285
|
333,35
|
0,5284
|
0,54156
|
353,75
|
0,7991
|
0;75854
|
373,25
|
0,8923
|
0,8875
|
394,65
|
0,9623
|
0,9533
|
413,15
|
1
|
0,9775
|
K(299,15) =14800 exp[-[-1,965ln(299,85 / 298,15) +0,011328 x 1,7 -71705 x(-1,272 10-7)-59297,9 x1,9015 10-5 ] / 8,314]=16869.
Kp = 4x2 / (1-x2) P.
16869 =4x2 / (1-x2) x1,015 105.
4x2 / (1-x2) =0,166 ; x2 / (1-x2) =0,0415.
x2(1+0,0415 )=0,0415 ; x =0,1997.
Une augmentation de température à pression constante favorise la dissociaion, celle-ci étant endothermique.
P(bar)
|
1
|
4
|
8
|
12
|
15
|
x
|
0,1875
|
0,0950
|
0,0673
|
0,0550
|
0,0492
|
Kp / (4P)= x2 / (1-x2).
x2(1+Kp / (4P) ) =Kp / (4P)
x2(1+0,1458 / 4) = 0,1458 /4 ;
1,03645 x2 =0,03645 ; x =0,1875.
Une augmentation de pression, à température constante est défavorable à
la dissociation.( en accord avec la loi de Le chatelier )
|
|
....
|
Calcul du pH d'une solution aqueuse.
On mesure le pH d'une solution d'acide acétique de concentration C=0,01 mol / L et on trouve 3,35.
1. Ecrire l'équation bilan de la réaction entre l'acide acétique est l'eau. Montrer que le pKa de cet acide vaut 4,7. Conclure.
CH3COOH aq + H2O(l) = CH3COO-aq + H3O+aq. (1)
Ka = [CH3COO-aq][H3O+aq] / [CH3COOH aq].
L'acide étant peu dissocié : Ka = [H3O+aq]2 / C.
[H3O+aq]2 = Ka C.
2 log([H3O+aq]) = log(Ka) + log (C).
2 pH = pKa - log (C).
pKa = 2 pH +log (C) = 2x3,35 +log(0,01) =4,7.
A pH inférieur à pKa, la forme acide CH3COOH prédomine.
2. Quel est le taux de dissociation de l'acide acétique ?
[H3O+aq] / C = 10-3,35 / 0,01 ~0,046.
3. Pourquoi l'acide acétique est-il très soluble dans l'eau ?
L'acide acétique est une molécule polaire ( présence du groupe COOH) ; il est donc soluble dans l'eau, solvant polaire.
4.
On considère une solution d'acétate de sodium (Na+ +CH3COO-) de concentration 0,01 mol / L. Quel est la valeur du pH ?
CH3COO- aq + H2O(l) = CH3COOH aq + HO-aq . constante K. (3)
2H2O =HO-aq + H3O+aq (2). Ke = 10-14.
CH3COO-aq + H3O+aq = CH3COOH aq + H2O(l) (4). 1 / Ka.
(2) +(4) donne (3)
K = Ke / Ka =[CH3COOH aq][HO-aq] / [CH3COO- aq].
CH3COO- aq ~ C, pour une base faible.
Ke / Ka ~[HO-aq]2 / C.
[HO-aq]2 = Ke C / Ka .
2 pOH = pKe -log C -pKa.
pOH = 0,5pKe -0,5log C -0,5pKa = 7-0,5 log(0,01) -0,5 x4,7 =5,65.
pH = 14 -pOH = 14-5,65 =8,35.
Ou encore : pH = 7 +½pKa +½log C= 7+2,35 -1=8,35.
|
|