Mouvements dans les champs de forces, concours d'entrée en première année de cycle ingénieurs filière sciences et  technologie 2021. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. .. .. . . .. .. ...... ... Etude d'un choc. ( 7 points). Un véhicule de masse M roulant à vitesse constante V0 sur une route rectiligne horizontale doit faire face brusquement à un obstacle prévu sur la chaussée pour éviter le choc. On se propose de calculer la distance de freinage et le temps d'arrêt nécessaire pour stopper le véhicule. On néglige l'effet du frein moteur et on suppose que le freinage s'effectue sans dérapage sous l'effet de la force de frottement constante des roues sur la chaussée Ff = -f Mg, où f est le coefficient de frottement moyen. On assimile la voiture à un point matériel dont la position G est représentée par sa coordonnée horizontale x dans le sens du mouvement avec x = 0 à la date t=0 du début de freinage. 1. Déterminer l'équation différentielle de la position x de G. La voiture est soumise à son poids, verticale vers le bas, valeur Mg, à l'action du plan, verticale vers le haut, valeur Mg et à la force de freinage, horizontale, opposée à la vitesse, valeur Ff. La seconde loi de Newton, en projection sur un axe horizontal, dans le sens du mouvement s'écrit : Md2x/dt2 =Ff. d2x/dt2 = -fg. 2. Déterminer le temps d'arrêt ta et la distance de freinage Da en fonction de V0, f et g. V =dx /dt = -fgt + A avec A une constante. A t=0 : V0 =A.  V =dx /dt = -fgt + V0. A l'arrêt V = 0 et ta = V0 /(fg). x = -½fgt2 + V0t +B avec B une constante. A t=0 : x =0. x = -½fgt2 + V0t. A l'arrêt : Da = -½fgta2 + V0ta. Da = -½V02/(fg) + V02/ (fg) =½V02/(fg). 3. Le temps de réflexe d'un conducteur est tr = 0,6 s. Le freinage débute à t = tr après avoir vu l'obstacle à la distance Da. Exprimer la vitesse de choc Vc du véhicule sur l'obstacle en fonction de V0, f, g , Da et tr. Distance parcourue avant freinage : V0tr. Distance de freinage : Da-V0tr . Variation de l'énergie cinétique : ½M(Vc2-V02). Travail de la force de freinage : -f Mg(Da-V0tr ). Théorème de l'énergie cinétique : ½M(Vc2-V02)=-f Mg(Da-V0tr ). Vc2-V02=-2fg(Da-V0tr ). Vc2=V02-2fg(Da-V0tr ). Vc =[ V02-2fg(Da-V0tr]½. 4. On fixe maintenant t=0 et x=0 au début du choc, la vitesse du véhicule étant Vc. On cherche à déterminer la durée du choc et l'intensité de la décélération brutale que subit le conducteur. L'enregistrement vidéo montre qu'entre le début et la fin du choc, G s'est déplacé d'une distance E. En supposant que l'accélération est constante et vaut -a durant tout le choc, exprimer la décélération a puis la durée théorique du choc tc en fonction de E et Vc. V =-at +Vc. tc =Vc / a. x = -½at2+Vct. E = -½atc2+Vctc. E = -½Vc2/a +Vc2/a =½Vc2/a. a=Vc2/(2E). Champ électrique.( 7 points). 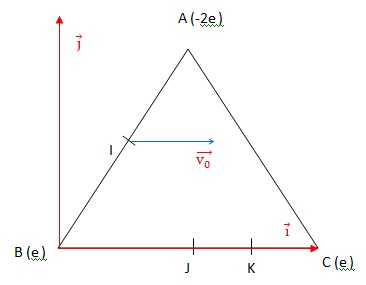Soit un triangle équilatéral direct ABC aux sommets duquel on place les charges SO42- en A, Na+ en B et K+ en C. I, J et K sont les milieux respectifs des segmennts [AB], [BC] et [JC]. Le champ électrique est supposé uniforme danns ce triangle et, sa valeur et sons sens sont le champ résultant créé par les trois charges au centre de  gravité G du triangle. Une particule de charge q pénètre dans le triangle au point I situé à 1 m de B avec une vitesse V0. Elle est ensuite soumise à l'influence du champ créé par les charges et  ressort en K. Masse de la particule m = 1,67 10-27 kg ; |q| =1,6 10-19 C.   1. Déterminer les caractéristiques du champ créé par les charges et en  déduire le signe de q. 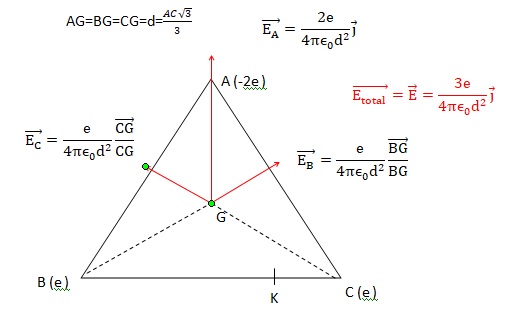BI = 1 m ; AB = 2 m ; d = 2 x3½ / 3 ~ 1,15 m ; |q| = e : E = 9 109 x 3 x 1,6 10-19 / 1,152~3,24 10-9 V / m. La déviation s'effectue vers le bas et le champ électrique est vertical vers le haut. Le vecteur force électrique et le vecteur champ électrique sont colinéaires de sens contraire :  donc q < 0. 2. Donner les équation horaires de cette particule et en déduire l'équation de la trajectoire. Poids : mg = 1,67 10-27 x 9,81 ~1,6 10-26 N. F=qE = 3,24 10-9 x 1,6 10-19 ~5,2 10-28 N. Le poids de la particule n' est pas négligeable devant la force électrique. Ecrire la seconde loi de Newton en projection sur les deux axes : ay =-eE / m -g ~ -10,1 m s-2 ; ax = 0. vy = -10,1 t ; vx = V0. y =-5,06 t2 +yI avec yI =3½/2 BI = 3½/2~0,867. y =-5,06 t2 +0,867. x = V0t +xI avec xI = ½. x = V0t +0,5. t = (x-0,5) / V0, repport dans y : y = -5,06 [(x-0,5) / V0]2 +0,867. 3. Déterminer V0. K( 0,75 BC  ; 0) soit (1,5 ; 0). yK = -5,06 [(xK-0,5) / V0]2 +0,867=0. [(xK-0,5) / V0]2 =0,867 / 5,06 =0,171. (xK-0,5) / V0=0,414. V0=1/ 0,414 ~2,4 m /s. 4. Combien de temps met la particule dans ce triangle ? xK = V0t +0,5. t = (xK-0,5) / V0 = 0,41 s. .... Modèle de la conduction électrique. 6 points. On considère un conducteur cylindrique d'axe Oz dont les charges mobiles sont des électrons animés d'une vitesse V sous l'action d'un champ électrique uniforme et indépendant du temps E colinéaire et de même sens que Oz que l'on applique à l'instant t=0. Les électrons sont soumis à une force de frottement de norme f = m V / t, t étant une constante et m la masse de l'électron. 1. Commet expliquez-vous l'existence des forces de frottement ?  Donner la dimension de t. le mouvement des électrons est ralenti par des collisions sur les coeurs d'atomes ( chocs des électrons libres sur les ions métalliques fixes  du réseau cristallin). t = m V / f avec m (kg) ; V (m s-1) et f (N soit kg m s-2). t s'exprime en seconde. 2. Déterminer l'équation horaire du mouvement des électrons. En déduire l'équation horaire de la vitesse. L'électron est soumis à la force électrique et aux forces de frottement, le poids étant négligeable devant celles-ci. Ecrire la seconde loi de Newton selon Oz : m dV / dt = eE -m V / t . dV /dt +V / t = eE / m. Solution de l'équation homogène dV /dt +V / t =0 : V =V0 exp(-t / t) avec V0 une constante. La vitesse limite est donnée par : Vl = eE t/ m.  Solution générale de l'équation différentielle : V =V0 exp(-t / t)+ eE t/ m. V(t=0) = 0 soit V0 =-eE t/ m. Par suite : V(t) =eE t/ m (1-exp(-t / t)). Equation horaire du mouvement des électrons, primitive de V(t) : z(t) =eE t/ m (t + t exp(-t / t)). 3. On pose V1 = etE / m, déterminer le temps t1 au bout duquel la vitesse de l'électron V est égale à V1 / 1000. t = 2,8 10-14 uSI. V(t) =Vl (1-exp(-t / t)). V1 / 1000 =Vl (1-exp(-t1 / t)). 0,001 = 1-exp(-t1 / t). exp(-t1 / t) =0,999. -t1 / t= ln(0,999)=-0,001. t1 ~2,8 10-17 s.

menu