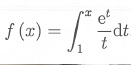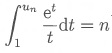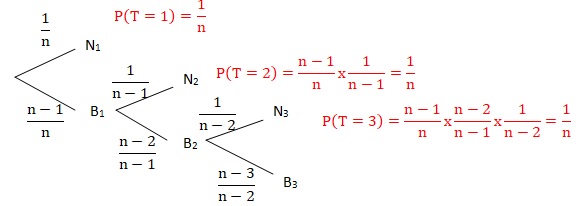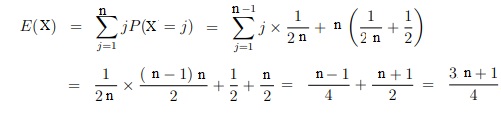Mathématiques,
fonctions, probabilités, Concours ITPE 2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
|
......
.....
|
Exercice 1.
Soit f la fonction définie sur R*+
à valeurs réelles telle que, pour tout x appartenant à R*+: 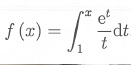
On ne cherchera pas à
calculer l'intégrale qui définit f(x).
1. Soit g la
fonction définie sur R*+ à valeurs réelles telle que, pour
tout x de R*+ : g(t) = et / t et G une primitive
de g sur R*+.
a. Justifier
l'existence de la fonction G.
La fonction exponentielle et et et la fonction 1/ t sont
continues sur R*+.
g(t), produit de deux fonctions continues sur R*+, est continue sur
R*+.
Toute fonction continue
sur un intervalle I admet une primitive sur cet intervalle.
b. Pout tout réel x
>0, exprimer f(x) à l'aide de la fonction G.
f(x) = G(x) - G(1).
c. Déduire de la
question précédente que f est dérivable sur R*+ et pour tout
réel x >0, calculer f '(x) où f ' désigne la dérivée de f.
f '(x) =G'(x)= g(x).
g(t), produit de deux fonctions dérivables sur R*+, est dérivable sur
R*+.
d. Calculer f(1).
f(1) = G(1)-G(1) = 0.
2.a. Etablir, pour
tout réel x >
1, l'inégalité f(x) >
e ln(x).
Etude du signe
de de f(x) - e ln(x).
On dérive : f '(x) -e / x = g(x) -e / x = (ex-e) / x.
Cette expression est positive ou nulle pour x > 1.
Donc la fonction f(x) - e ln(x) est strictement croissante pour x >
1.
De plus f(1) = 0 ; donc
f(x) > e
ln(x).
b. En déduire la
limite de f(x) en plus l'infini.
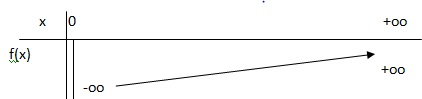
En plus l'infini : ln(x) tend vers plus l'infini ;
e étant positif, e ln(x) tend vers plus l'infini.
Quand x tend vers plus l'infini, f(x) tend vers plus l'infini.
3.a. Etablir, pour
tout réel x de l'intervalle ]0 ; 1 ], l'inégalité f(x) < ex ln(x).
Etude du signe
de de f(x) - ex ln(x).
On dérive : f '(x) -(ex ln(x)+ex / x) = g(x) -ex
ln(x)-ex / x = -ex
ln(x)
Sur ]0
; 1 ] ex > 0 et ln(x) < 0 ; ex
ln(x) < 0 ; -ex ln(x) > 0 ;
Donc la
fonction f(x) - ex ln(x) est strictement croissante sur
]0 ; 1 ].
De plus f(1) = 0 ; donc
f(x) < ex
ln(x).
b. En déduire la
limite de f(x) en 0+.
Quand x tend vers 0+, ex
>0 et ln(x) tend vers moins l'infini.
ex ln(x) tend
vers moins l'infini.
Quand x tend
vers 0+, f(x) tend vers moins l'infini.
4.a
Dresser le tableau de variation de f.
b. Etudier les variations de f '.
f '(x) = g(x) = ex / x.
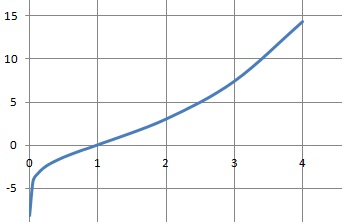
Sur R*+, f '(x) > 0, donc f(x) est strictement croissante.
c. Donner l'allure du graphe de f.
Remarque
: développement limité de ex : 1 +x +x2/2 +x3/
6 +x4 /24+...
g(x) = ex / x =1
/x +1 +x/2 +x2/ 6 +x3 /24+...
G(x) =ln(x) +x +x2/4
+x3/ 18 +x4 /96+...
g(1) =1 +0,25 +1 /18 + 1 /96 +... ~1,316.
f(x) = ln(x)
+x +x2/4
+x3/ 18 +x4 /96 -1,316.
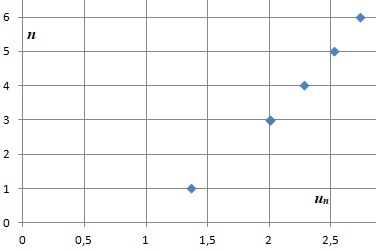
5.a Montrer que
pour tout n entier naturel, il existe un unique réel, noté un
vérifiant 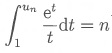
b. En utilisant les variations de la
fonction f, montrer que la suite (un) n>0 est croissante.
c. Déterminer la
limite de un en plus l'infini.
f(x) est strictement croissante sur R*+.
f(1) = 0.
n
appartient à R*+.
D'après
le corollaire du théorème des valeurs intermédiaires,il
existe un unique réel, noté un vérifiant 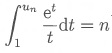
un tend vers plus
l'infini quant n tend vers plus l'infini.
|
...
|
|
|
....
|
Exercice 3.
n désigne un entier naturel supérieur ou égal à 3.
On dispose de deux urnes U1 et U2 indiscernables
contenant chacune n boules indiscernables au toucher.
L'urne U1 contient (n-1) boules blanches et une boule noire.
L'urne U2 contient n boules blanches.
A - Temps
d'attente dans l'urne 1.
On effectue des tirages sans remise dans l'urne U1, jusqu'à
l'obtention de la boule noire.
On note T la variable aléatoire qui prend pour valeur le nombre de
tirages nécessaires pour l'obtention de la boule noire.
On notera, pour tout entier naturel i appartenant à [1 ; n], Ni
l'événement " on tire une boule noire lors du i-ème tirage" et Bi
l'événement " on tire une boule blanche lors du i-ème tirage".
1. Rappeler la
formule des probabilités composées.
Soient A1, ..., An des événements dont
l'intersection est de probabilité différente de zéro.
P(A1 n ...n An) = P(A1) x P A1(A2)
x ... PA1 n ... n An-1(An)
2. En écrivant
soigneusement les événements utilisés, calculer P(T=1), P(T =2) et P
(T=3).
P(T=1) = 1 / n ; un cas favorable sur n cas possibles.
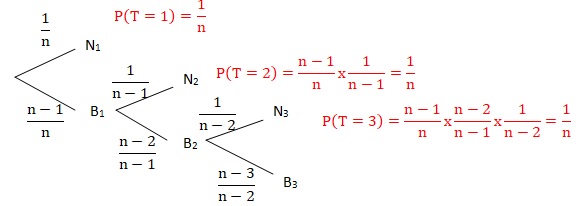
3. Déterminer la
loi de la variable aléatoire T.
Il s'agit de la loi uniforme sur [ 1 ; n ].
4. Préciser le
nombre moyen de tirages nécessaires à l'obtention de la boule noire.
L'espérance de cette loi uniforme est E(T) = (n+1) / 2.
B. Une seconde expérience
aléatoire.
On choisit l'une des deux urnes au hasard ( chacune a la même
probabilité d'être choisie ) et on tire dans l'urne choisie une par une
les boules sans remise jusqu'à être en mesure de pouvoir connaître
l'urne choisie.
On note X la variable aléatoire qui prend pour valeur le nombre de
tirages ainsi effectués. On note A1 l'événement " l'urne U1
a été choisie ".
On note A2 l'événement " l'urne U2 a été choisie
".
5. Que vaut P(A1)
?
On sera en mesure de déterminer s'il s'agit de l'urne U1 dès
l'obtention de la boule noire. D'après la question précédente P(A1)
= 1 / n.
6. Montrer que pour
tout entier j appartenant à [1 ; n], PA1(X=j) = 1 / n.
On sera en mesure de déterminer s'il s'agit de l'urne U1 dès
l'obtention de la boule noire. D'après la question précédente PA1(X=j)
= 1 / n.
7. Calculer PA2(X=j).
L'urne U2 ne contient que des boules blanches. Tant que
cette urne n'est pas vide, on ne peut pas être certain qu'on ne va pas
tirer une boule noire.
PA2(X=j) = 0 si 1 <
j < n-1 ; PA2(X=j)
= 1 si j = n.
8. Montrer que P(X
= j) =1 / (2n) si 1 <
j < n-1 et P(X =
j) =1 / (2n) + 0,5 si j = n.
On utilise la formule des probabilités totales :
P( X=n) = PA1(X=n)P(A1) +PA2(X=n) P(A2)
= 1 / (2n) + 0,5 si j = n.
Comme PA2(X = j) = 0 si 1 < j < n-1, la même
formule donne P(X = j) =1 / (2n) si 1 < j < n-1.
9. Calculer
l'espérance de X.
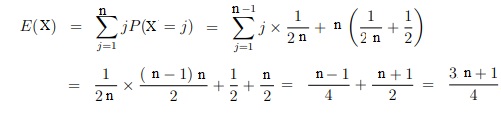
|
|