Mathématiques,
QCM, fonction, suite, probabilités, géométrie.
enseignement de spécialité première générale.
|
.
.
|
|
Sujet 29
Exercice 1.
( 5 points ).
QCM ( aucune justification n'est demandée).
1. L’arbre pondéré ci-dessous représente une situation où A,B,C et D sont des évènements d’une expérience aléatoire :
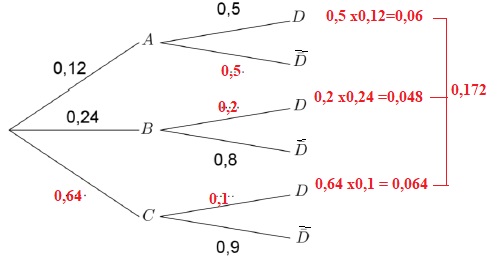
La probabilité de l’évènement D est égale à : a) 0,06 ; b) 0,8 ; c) 0,5 ; d) 0,172 vrai.
2. L’ensemble des solutions réelles de l’inéquation −2x2−5x+3< 0 est :
a) ]−3 ;1 / 2[ ; b) ]−∞ ;−3[∪]1 / 2 ;+∞[ ; c) ]−∞ ;−1 / 2[∪]3 ;+∞[ ; d) ]−1 / 2 ;3[
Solutions de -2x2-5x+3 =0 ; discriminant :(-5)2-4*3*(-2)=49=72 ; x = (5-7)/ (-4)=0,5 et x = (5+7)/(-4)= -3
3. On considère la droite D d’équation 2x−8y+1=0.
Les coordonnées d’un vecteur normal à D sont :
a) (1; −4) vrai ; b) (8; −2) ; c) (−8 ; 2) ; d) (−4 ; 1).
4. Dans un repère orthonormé, l’équation du cercle de centre A (-2 ; -4) et de rayon 2 est :
a) x2−4x+y2−8y+16=0
b) x2+4x+y2+8y+16=0
c) x2−4x+y2−8y+18=0
d) x2+4x+y2+8y+18=0
(x+2)2 +(y+4)2 = 4 ; x2+4x+4+y2+8y+16 = 4 ; x2+4x+y2+8y+16=0. Réponse b.
5. On considère la suite (un) définie par :
u0=1 et pour tout entier naturel non nul n, un+1=un +2n−3
a) u1=0. Vrai. u1=u0 +2−3 = 0
b) (un) est arithmétique. Faux. un+1-un = 2n-3 diffère d'une constante.
c) u3=−2. Faux. u2 =u1+4-3= 1 ; u3 =u2+6-3= 4;
d) (un) est décroissante. Faux. un+1-un =2n−3
Sujet 30.
1. L’inéquation 2x2−9x+4 ≥0 a pour ensemble de solutions :
a. 𝑆=[0,5 ; 4]
b. 𝑆=]−∞ ; 0,5]∪[4 ;+∞[
c. 𝑆=∅
d. 𝑆=]−∞ ; -4]∪[−0,5 ;+∞[.
Solutions de 2x2−9x+4 =0 : discriminant : (-9)2 -4*2*4=49 = 72 ; x =(9-7) / 4 = 0,5 et x = (9+7) / 4 = 4. Réponse b.
2. On considère la fonction 𝑔 définie sur l’ensemble des réels R par g(x)=−x2+4x, alors
a. le minimum de la fonction g sur R est 4
b. le maximum de la fonction g sur R est 4
c. le maximum de la fonction g sur R est 2
d. g est décroissante sur l’intervalle [4 ;+∞[ .
g'(x) = -2x+4 ; g '(2)=0.
g'(x) < 0 si x > 2 et g(x) est strictement décroissante.
g'(x) > 0 si x < 2 et g(x) est strictement croissante.
g'(2)=0 ; g(x) présente un maximum pour x = 2. g(2) = -4+8 = 4. Réponse b.
3.
Le plan est rapporté à un repère orthonormé. La droite passant par le
point A(0 ;−7) et de vecteur normal dont les coordonnées sont (2 ; −5)
a pour équation
a. 2x−5y−35=0
b. 2x−5y+35=0
c. −5x−2y+14=0
d. 5x+2y+14=0.
Equation de la droite 2x-5y+d = 0.
A appartient à la droite : 0 -5(-7)+d=0; d = -35 ; 2x-5y-35=0. Réponse a.
4. Le plan est rapporté à un repère orthonormé. L’ensemble des points M de coordonnées (x ; y) telles que x2−4x+y2+6y=12 est
a. le point de coordonnées (5;1)
b. le cercle de centre A(2;−3) et de rayon √12
c. le cercle de centre A(2;−3) et de rayon 5
d. le cercle de centre B(−2;3) et de rayon 5.
(x-2)2 -4 +(y+3)2-9 = 12 ; x2−4x+y2+6y=25 = 52. Réponse c.
5. Le plan est muni d’un repère orthonormé.
On considère la droite d d’équation 2x+3y−1=0.
a) La droite d est perpendiculaire à la droite (AB), où A(−2 ; 3) et B(2 ; 9). Vrai.
Coefficient directeur de la droite (AB) : (yA-yB) / (xA-xB) = -6 / (-4) =1,5.
y = 1,5 x+b ; A appartient à cette droite : 3 = 1,5*(-2) +b ; b = 6.
y = 1,5 x +6 soit 3x-2y+12=0.
b) Le vecteur de coordonnées (−3 ; 2) est un vecteur normal à la droite d. Faux ( il aurait fallu écrire 2 ; 3)).
c) La droite perpendiculaire à d passant par le point C(−1 ; 2) admet pour équation 3x−2y+1=0. Faux.
3*(-1)-2*(2)+1 = -6 diffère de zéro.
d) La droite parallèle à d passant par le point D (2 ; 3) admet pour équation 2x+3y+13=0. Faux.
Equation de cette droite : 2x +3y +c = 0 ; D appartient à cette droite :4+9+c = 0 ; c = -13.
Réponse a.
|
|
Exercice 2. ( 5
points) Sujet 29. La répartition des 150 adhérents d’un club de sport est donnée dans le tableau ci-dessous :
Age
|
15 ans
|
16 ans
|
17 ans
|
18 ans
|
Nombre de filles
|
17
|
39
|
22
|
10
|
Nombre de garçons
|
13
|
36
|
8
|
5
|
Total
|
30
|
75
|
30
|
15
|
On choisit un adhérent au hasard.
1. Quelle est la probabilité que l’adhérent choisi ait 17 ans ?
30 / (30+75+30+15)=30 / 150=0,2.
2. L’adhérent choisi a 18 ans. Quelle est la probabilité que ce soit une fille ?
10 / 15 =2 /3.
On note X la variable aléatoire donnant l’âge de l’adhérent choisi.
3. Déterminer la loi de probabilité de X.
xi
|
15
|
16
|
17
|
18
|
p(X=xi)
|
30 / 150 =0,2
|
75 / 150 = 0,5
|
0,2
|
0,1
|
4. Calculer P(X ≥ 16) et interpréter le résultat.
P(X ≥ 16) = 1-0,2 = 0,8.
80 % des adhérents sont agés de16 à 18 ans.
5. Calculer l’espérance de X. Interpréter le résultat.
E(X) =0,2 x15 +0,5 x16 +0,2 x17 +0,1 x18 =3 +8 +3,4 +1,8 =16,2.
L'âge moyen des adhérents est 16,2 ans.
Sujet 30.
On considère la fonction f définie sur R par f(x)=(2x−1)ex.
On note f ′ la fonction dérivée de la fonction f.
1. Montrer que pour tout réel x, f ′(x)=(2x+1)ex.
On pose u = 2x-1 et v = ex ; u' = 2 ; v' = ex.
u'v +v'u = 2ex+(2x-1)ex =(2x+1)ex.
2. Étudier le signe de f ′(x) sur R.
ex est toujours positif.
f '(-0,5) = 0.
Si x > -0,5, f '(x) >0 et f(x) est strictement croissante.
Si x < -0,5, f '(x) <0 et f(x) est strictement décroissante.
Si x = -0,5, f'(x)=0 et f(x) présente un minimum.
3. En déduire le tableau de variation de la fonction f sur R.
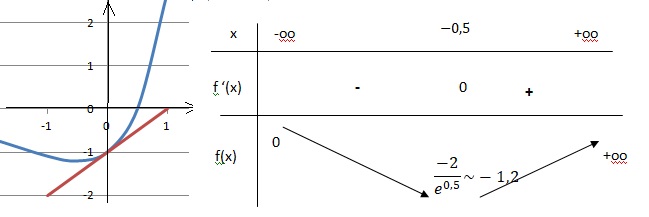
Dans les questions suivantes, on note C la courbe représentative de la fonction f dans un repère.
4. Déterminer les coordonnées du point d’intersection de C avec l’axe des ordonnées.
x =0 ; f(0) = -e0 = -1.
5. Déterminer une équation de la tangente T à C au point d’abscisse 0.
Coeficient directeur de T : f '(0) =1.
Equation de T : y = x+b.
La tangente passe par le point de coordonnées ( 0 ; -1).
-1 = 0 +b ; y = x-1.
|
|
Exercice 3. ( 5 points).
Sujet 29.
La concentration d’un médicament dans le sang en mg.L−1 au cours du temps t, exprimé en heure, est modélisée par la fonction f définie sur [0;+∞[ par : f(t) = t e−0,5t dont la représentation graphique est donnée ci-dessous. 1. Calculer la valeur exacte de f(4) et interpréter le résultat dans le contexte de l’exercice.
f(4) =4 e-2.
Au bout de 4 heures, la concentration du médicament dans le sang est 4 e-2 mg / L.
2. On note f ′ la fonction dérivée de f.
Montrer que pour tout t ∈[0;+∞[, f ′(t)=(1−0,5t)e−0,5t.
On pose u = t et v = e-0,5t ; u' = 1 ; v' = -0,5e-0,5t.
u'v +v'u = e-0,5t -0,5te-0,5t = (1−0,5t)e−0,5t.
3. Étudier le signe de f ′(t) sur [0;+∞[.
e−0,5t est toujours positif.
Si t < 2, f '(t) >0 et f(t) est strictement croissante.
Si t > 2, f '(t) < 0 et f(t) est strictement décroissante.
Si t =2, f '(t) = 0 et f(t) présente un maximum.
4. Déduire de la question précédente le tableau de variations de la fonction f sur [0;+∞[.
5. Quelle est la concentration maximale du médicament dans le sang ? On donnera la valeur exacte, puis une valeur approchée à 10−2 près.
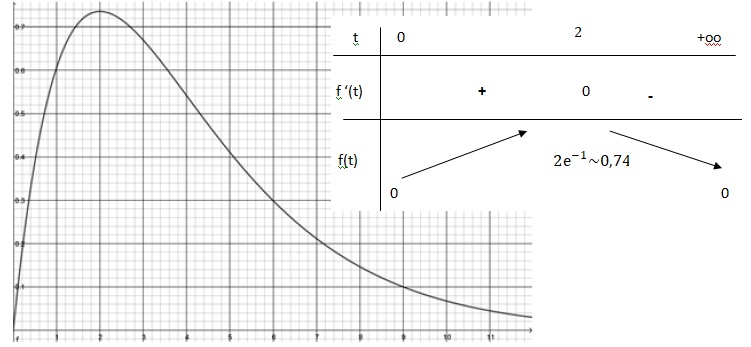 Sujet 30.
On
appelle pourcentage de compression d’une image, le pourcentage de
réduction de sa taille en ko (kilo-octets) après compression.
Une image a une taille initiale de 800 ko. Après une première compression, sa taille est de 664 ko.
1. Calculer le pourcentage de réduction associé à cette première compression.
664 / 800 =0,83 ; pourcentage de réduction 1-0,83 =0,17 ( 17 %).
Dans la suite de l’exercice, on fixe le pourcentage de réduction à 17%.
On effectue n compressions successives. Pour tout entier naturel n, on note tn la taille de l’image en ko après n compressions.
On a donc t0=800.
2. Pour tout entier naturel n, exprimer tn+1 en fonction de tn et en déduire la nature de la suite (tn).
tn+1 = 0,83 tn, suite géométrique de raison 0,83 et de premier terme 800.
3. Pour tout entier naturel n, exprimer tn en fonction de n.
tn = 800 * 0,83n.
Afin de déterminer le nombre minimal de compressions successives à
effectuer pour que cette image ait une taille finale inférieure à 50
ko, on considère la fonction
Python suivante :
def nombreCompressions(A)
t=800
n=0
while t > A :
t=t*0,83
n=n+1
return n
4. Préciser, en
justifiant, le nombre A de sorte que l’appel nombreCompressions(A)
renvoie le nombre de compressions successives à effectuer que l’on
cherche à déterminer.
A = 50.
5. Quel est le
nombre minimal de compressions successives à effectuer pour que ce
fichier ait une taille finale inférieure à 50 ko ?
n
|
13
|
14
|
15
|
taille (ko)
|
71
|
58,9
|
48,9
|
Il faut réaliser 15 compressions.
|
|
Exercice 4. ( 5 points) Sujet 29 Un
téléphone coûte 600 euros lors de son lancement. Tous les ans, le
fabricant sort une nouvelle version de ce téléphone. Le prix de ce
téléphone augmente de 3 % chaque année.
On note un le prix du téléphone en euros n années après son lancement. On a donc u0=600.
1. Calculer u1 et u2. Interpréter les résultats.
u1 = 600 x1,03 =618 €, prix du téléphone un an plus tard.
u2 = 618 x1,03 =636,54 €, prix du téléphone 2 ans plus tard.
2. Exprimer un+1 en fonction de un, pour tout entier naturel n et en déduire la nature de la suite (un). Préciser sa raison et son premier terme.
un+1 = 1,03 un, suite géométrique de raison 1,03 et de premier terme 600.
3. Exprimer, pour tout entier n, un en fonction de n.
un = 600 x1,03n.
4. Recopier et
compléter sur la copie la fonction Python ci-dessous pour qu’elle
détermine le nombre minimum d’années nécessaires afin que le prix du
téléphone dépasse 1000 euros.
def nombreAnnees():
n=0
u=600
while u < 1000
n = n+1
u = u*1,03
return n
5. 5. Quelle est la valeur de 𝑛 renvoyée par cette fonction Python ?
600 x1,0317 =991,71 ; 600 x1,0318 =1021,46.
n = 18.
|
Sujet 30.
Dans un jeu, Jeanne doit trouver la bonne réponse à une question posée.
Les questions sont classées en trois catégories : sport, cinéma et musique.
Jeanne, fervente supportrice de ce jeu, est consciente qu’elle a :
1 chance sur 2 de donner la bonne réponse sachant qu’elle est interrogée en sport ;
3 chances sur 4 de donner la bonne réponse sachant qu’elle est interrogée en cinéma ;
1 chance sur 4 de donner la bonne réponse sachant qu’elle est interrogée en musique.
On note :
S l’événement : « Jeanne est interrogée en sport » ;
C l’événement : « Jeanne est interrogée en cinéma » ;
M l’événement : « Jeanne est interrogée en musique » ;
B l’événement : « Jeanne donne une bonne réponse ».
Dans chaque catégorie, il y a le même nombre de questions. On admet donc que P(S)=P(C)=P(M)=1 / 3.
1. Construire un arbre pondéré décrivant la situation.
2. Jeanne tire au hasard une question. Montrer que P(B)=1 /2.
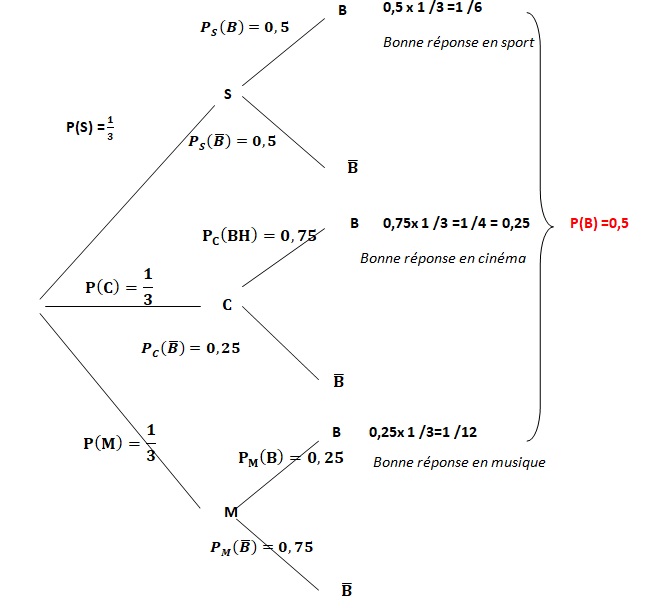
2. Jeanne tire au hasard une question. Montrer que P(B)=1 /2.
Pour participer à ce jeu, Jeanne doit payer 10 € de droit d’inscription. Elle recevra :
10 € si elle est interrogée en sport et que sa réponse est bonne ;
20 € si elle est interrogée en cinéma et que sa réponse est bonne ;
50 € si elle est interrogée en musique et que sa réponse est bonne ;
rien si la réponse qu’elle donne est fausse.
On note X la variable aléatoire qui, à chaque partie jouée par Jeanne
associe son gain algébrique, c’est-à-dire la différence en euros entre
ce qu’elle reçoit et les 10 € de droit d’inscription.
3. Montrer que P(X=40)=1/12.
Une bonne réponse en musique rapporte 50 € ; droit d'inscription 10 € : bilan 40 €.
Donc P(X = 40 = 1 /12.
4. Déterminer la loi de probabilité de X.
xi
|
-10
|
0
|
10
|
40
|
P(X =xi)
|
0,5
|
1 / 6
|
0,25
|
1 /12
|
5. Calculer l’espérance mathématique de X. Jeanne a-t-elle intérêt à jouer ?
E(X) = -10 x0,5 +10 x0,25 +40 /12 ~ -5 +2,5 +3,33 ~0,83 €.
Le gain est faible, on a peu d'intérêt à jouer.
|
|