Mathématiques,
QCM, fonction, suite, probabilités, géométrie.
enseignement de spécialité première générale.
|
.
.
|
|
Sujet 35
Exercice 1.
( 5 points ).
QCM ( aucune justification n'est demandée).
1. L'ensemble des solutions de l'inéquation 3x2−4x+1 ≥0 est :
a) ]−∞;−1]∪[−13;+∞[ ; b) ]−∞;1 / 3]∪[1;+∞[ ; c) ]−∞;−1 / 3]∪[1;+∞[ ; d) [1 / 3;1]. Réponse b.
a est positif, la parabole présente un minimum.
Solutions de 3x2−4x+1 =0 : discriminant D =(-4)2 -4*1*3=4 = 22.
x1 =(4+2) / 6 =6 / 6 = 1 ; x2 =(4-2) /6 =2/6 = 1 /3.
2. Dans
le plan muni d'un repère orthonormé, on considère les vecteurs de
coordonnées (a+2; −1) et (3 ; a ), où a est un nombre réel. Les
vecteurs sont orthogonaux si, et seulement si :
a) a(a+2) -3=0 ; b) a(a+2)+3 =0 ; c) 3(a+2) -a = 0 ; d) 3(a+2)+a=0.
3(a+2) +(-1) a = 3(a+2)-a=0. Réponse c.
3.
Dans le plan muni d'un repère orthonormé, on considère le point A (−2 ;
3) et le vecteur de coordonnées (1 ; 2). Une équation cartésienne de la
droite d passant par le point A et de vecteur normal de coordonnées (1
; 2) est :
a) -2x+y-7=0 ; b) x+2y -4=0 ; c) x-2y +8=0 ; d) 2x+y+1=0.
Equation de la droite d : x+2y +d = 0.
A appartient à cette droite : xA +2yA +d = 0 ; -2 +2*3+d =0 ; d = -4 ; x+2y-4=0. Réponse b.
4. On considère la suite (un), géométrique de raison 2 et de premier terme u0=3.
La somme u0+u1+⋯+u10 est égale à :
a) 3(211-1) ; b) 3(1-211) : c) 3(210-1) ; d) 3(1-210).
u0(1-211) / (1-2) =3(211-1). Réponse a.
5. Soit
f la fonction définie et dérivable sur ]1;+∞[ par f(x)=(2x+1) / (x-1).
La fonction dérivée de f sur ]1;+∞[ a pour expression :
a) f '(x) = -1 /(x-1)2 ; b) f '(x) = -3 /(x-1)2 ; c) f '(x) = (4x-1) /(x-1)2 ; d) f '(x) = 1 /(x-1)2 .
On pose u =2x+1 et v = x-1 ; u' = 2 ; v' = 1 ; (u'v-v'u) / v2 =(2(x-1)-(2x+1)) / (x-1)2 = -3 /(x-1)2. Réponse b.
Sujet 36.
1. Dans le plan rapporté à un repère orthonormé, on considère la droite D d'équation cartésienne 4x + 5y – 7 = 0.
Un vecteur normal à D a pour coordonnées :
a. (5 ; 4) ; b. (−5 ; 4) ; c. (4 ; 5) ; d. (4 ; −5). Réponse c.
2. Dans le plan rapporté à un repère orthonormé, l'ensemble E des points M de coordonnées (x ; y) vérifiant : x2 – 2x + y2 = 3 est un cercle :
a. de centre A(1 ; 0) et de rayon 2.
b. de centre A(1 ; 0) et de rayon 4.
c. de centre A(−1 ; 0) et de rayon 2.
d. de centre A(−1 ; 0) et de rayon 4. Réponse a.
x2 – 2x + y2 =x2 – 2x +1-1+ y2 =(x-1)2 +y2 = 3+1=4.
3. La somme 15 + 16 + 17 + … + 243 est égale à :
a. 29 403 ; b. 29 412 ; c. 29 541 ; d. 29 646. Réponse c.
Suite arithmétique de raison 1 et de premier terme15.
Somme des 229 termes : 229(15+243) / 2 = 29541.
4. On considère la fonction f dérivable définie sur R par f (x)= (x + 1)ex.
La fonction dérivée f ’ de f est définie sur R par :
a. f ′(x) = (x + 2)ex ; b. f ′(x) = (x + 1)ex ; c. f ′(x) = xex ; d. f ′(x) =ex Réponse a.
On pose u = x+1 et v = ex ; u' = 1 ; v' = ex ; u'v+v'u =ex+(x+1)ex =(x + 2)ex .
5. En utilisant l’arbre de probabilité pondéré ci-dessous, on obtient :
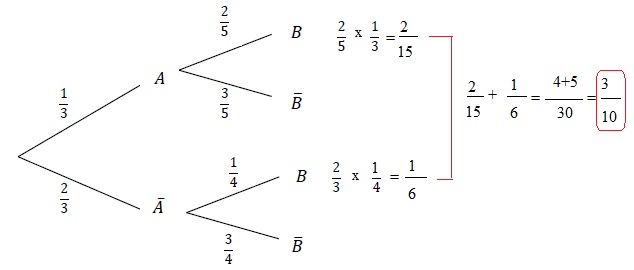
a. P (B) = 1 / 4 ; b. P (B) = 2 / 5 ; c. P (B) = 13 / 20 ; d. P (B) = 3 / 10
Réponse d.
|
|
Exercice 2. ( 5
points) Sujet 35. Un
organisme de vacances propose des séjours en France et à l'étranger
pour des jeunes. Ces derniers sont répartis en deux catégories suivant
leur âge : adolescents ou jeunes enfants. 40 % des participants sont
des adolescents et parmi eux, 70 % choisissent un séjour à l'étranger.
Parmi les jeunes enfants, 90 % choisissent un séjour en France.
On interroge au hasard un participant à un séjour de cet organisme.
On note A l'événement "le participant est un adolescent", et F l’événement "le participant choisit un séjour en France".
1. Recopier et compléter sur la copie les branches de l'arbre de probabilité ci-dessous pour qu'il représente la situation.
2. Calculer la probabilité que le participant soit un adolescent et qu'il choisisse un séjour à l'étranger.
3. Montrer que la probabilité qu'un participant choisisse un séjour à l'étranger est 0,34.

4. Calculer la
probabilité que le participant ne soit pas un adolescent, sachant qu'il
part à l'étranger. Donner la valeur arrondie au centième de cette
probabilité.
Pnon F(non A) =P(non A n non F) / P(non F) =0,06 / 0.34 ~0,18.
5. On interroge au
hasard, et de manière indépendante, deux participants à des séjours de
cet organisme pour connaitre s'ils ont choisi un séjour en France ou
non. L’organisation de ce sondage est telle qu’une même personne peut
être interrogée deux fois. Calculer la probabilité qu'au moins un des
deux participants ait choisi un séjour en France. Donner cette
probabilité arrondie au centième.
P(F) = 0,12 +0,54 = 0,66.
On définit une variable aléatoire X prenant pour valeurs le nombre de voyages en France.
Au moins un signifie X = 1 ou X = 2.
X suit la loi binomiale de paramètre p = 0,66 et avec N = 2.
1-P(X=0)=1-0,1156 ~0,88.
Sujet 36.
Dans un repère orthonormé du plan, on considère les points A (2 ; −1), B (0 ; 3) et C (3 ; 1).
1. a. Vérifier que le produit scalairre suivant est égal à 6.
b. Calculer AB et AC, on donnera les valeurs exactes.
c. Vérifier que cos(BAĈ)= 0,6 et en déduire la mesure de l'angle BAĈ au degré près.
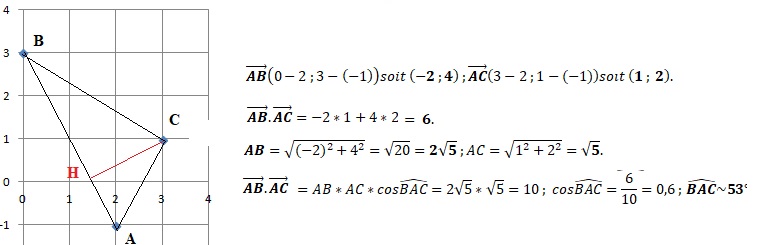
2. a. Vérifier qu’une équation cartésienne de la droite (AB) est 2x+y−3=0.
y = ax +b.
A appartient à cette droite : yA = axA +b ; -1=2a+b.
B appartient à cette droite : yB = axB +b ; 3=0+b.
Par suite a= (-1-3) / 2 = -2.
y = -2x+3 soit 2x+y-3=0.
b. On note H le pied la hauteur du triangle ABC issue du sommet C. Déterminer les coordonnées du point H.
H appartient à la droite AB : 2xH +yH -3 = 0 soit yH =3-2xH.
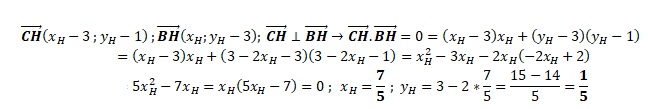
|
|
Exercice 3. ( 5 points).
Sujet 35.
Une
commune compte 800 habitants au début de l’année 2019. Le maire prévoit
une baisse de 2 % par an du nombre d’habitants à partir de 2019.
Pour tout entier naturel n, on note un le nombre d’habitants n années après 2019. Ainsi, u0=800 et pour tout entier naturel, un+1=0,98 un.
1. Calculer u1 et préciser ce que cette valeur représente dans le contexte de l'exercice.
u1 = 0,98 u0 = 0,98 x 800 =784.
En 2020, la commune comptera 784 habitants.
2. Préciser la nature de la suite (un) ainsi que sa raison.
Suite géométrique de raison 0,98 et de premier terme u0 = 800.
3. Déterminer, pour tout entier naturel n, l’expression de un en fonction de n.
un = u0 * 0,98n = 800 *0,98n.
4. Calculer une valeur approchée, à l’entier près, du nombre d’habitants dans cette commune en 2025.
n = 6 ; u6 = 800 *0,986 ~709.
5. Recopier et
compléter sur la copie la fonction écrite en langage Python ci-dessous,
afin qu’elle permette de calculer, pour tout entier naturel n, le terme
un.
def u(n) :
u =800
for i in range (1, n)
u = 0,98*u
return u
Sujet 36.
En
1995, le taux de scolarisation des jeunes de 18 ans atteignait 84,8 %,
du fait d’une forte progression de la poursuite d’études dans le second
cycle général et technologique jusqu’au baccalauréat.
Une étude de l’INSEE montre que ce taux de scolarisation a régulièrement diminué au cours des dix années suivantes.
On considère que la diminution du taux de scolarisation à 18 ans est chaque année de 1 % à partir de 1995.
Pour tout entier naturel n, on modélise le taux de scolarisation des jeunes de 18 ans en 1995 + n, par une suite (un) ; ainsi u0=84,8.
1. Quel est le taux de scolarisation des jeunes âgés de 18 ans en 1996 ?
u1 = u0(1-1 /100) =0,99 u0 = 0,99 x84,8 = 83,952.
2. Déterminer, en justifiant, la nature de la suite (un).
un+1 / un = 0,99 ; suite géométrique de raison 0,99 et de premier terme u0 = 84,8.
3. On donne le programme suivant en langage Python :
u = 84,8
n =0
while u > 80 :
u = 0,99 *u
n=n+1
Déterminer la valeur numérique que contient la variable n à l’issue de
l’exécution du programme. Interpréter cette valeur dans le contexte de
l’énoncé.
u6=79,83 ; u5 = 80,64.
n = 6 ; en 2001, le taux de scolarisation des jeunes de 18 ans sera inférieur à 80 %.
4. Exprimer, pour tout entier naturel n, un en fonction de n.
un = u0 *0,99n=84,8 *0,99n.
5. Quel est le taux de scolarisation des jeunes de 18 ans en 2005 ?
n = 10 ; u10 =84,8 *0,9910 ~76,7 %.
|
|
Exercice 4. ( 5 points) Sujet 35 Partie A : lecture graphique
1. Dans le plan muni d’un repère orthonormé, Cf est la courbe représentative d’une fonction f, définie et dérivable sur l'ensemble R des nombres réels.
Les points A et B sont les points de Cf d’abscisses respectives −2 et 0, et on a tracé les tangentes à Cf en ces points.
On suppose que la tangente en A est parallèle à l'axe des abscisses et que la tangente en B passe par le point C(1 ; 6).
On note f ′ la fonction dérivée de f.
Lire graphiquement les valeurs de f ′(−2) et f ′(0). Justifier brièvement.
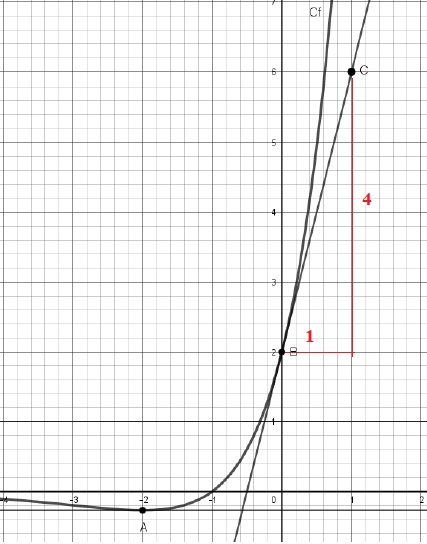
f '(-2) =0, la tangente à la courbe est horizontale.
f '(0) = coefficient directeur de la tangente à la courbe en B = 4.
Partie B : Calcul algébrique
La fonction représentée sur le graphique précédent est la fonction f définie sur l'ensemble R des nombres réels par : f(x)=ex(2x+2)
On admet que f est dérivable sur R.
2. Montrer que pour tout nombre réel x, f ′(x)=ex(2x+4).
On pose u = ex et v = (2x+2) ; u' = ex et v' = 2 ; u'v+v'u=ex(2x+2) +2ex =ex(2x+4).
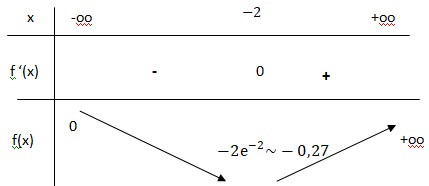
3. Étudier le signe de f ′ sur R, puis en déduire le tableau de variation de f sur R.
ex est toujours positif.
Si x < -2, f '(x) <0 et f(x) est strictement décroissante.
Si x > -2, f '(x) >0 et f(x) est strictement croissante.
Si x = -2, f '(x) =0 et f(x) présente un minimum.
4. Déterminer par le calcul, l’équation réduite de la tangente à Cf au point d’abscisse 0.
Coefficient directeur : f '(0) =4 ; y = 4x +b.
B( 0 ; 2) appartient à la tangente : 2 = 4*0+b ; b = 2 ; y = 4x+2.
5. Justifier par le
calcul les deux résultats suivants admis au début de l’exercice : - La
tangente en A est parallèle à l'axe des abscisses. - La tangente en B
passe par le point C(1;6).
En A, f '(-2) = 0, la tangente est horizontale.
yC = 6 ; xC+4 = 2+4 = 6 ; yC = 4xC+2. C appartient à la tangente à la courbe en B.
|
Sujet 36.
Soit f la fonction dérivable définie sur [−3 ; 3] par f(x) = 2x3 + 2x2
– 2x + 1. On note C sa courbe représentative dans un repère donné.
1. Déterminer f ′(x), où f ’ est la fonction dérivée de f sur [−3 ; 3].
f '(x) =6x2+4x-2.
2. Étudier le signe de f ’(x) sur [−3 ; 3].
Solutions de 6x2+4x-2=0 ; discriminant D = 42-4*6*(-2)=64 = 82.
x1 = (-4-8) / 12 = -1 ; x2 =(-4+8) /12 =1 /3.
f '(x) = 6(x+1)(x-1 / 3).
3. Dresser le tableau de variations de f sur [−3 ; 3]. Les valeurs aux
bornes pourront être données en valeur approchée à 10-2 près.
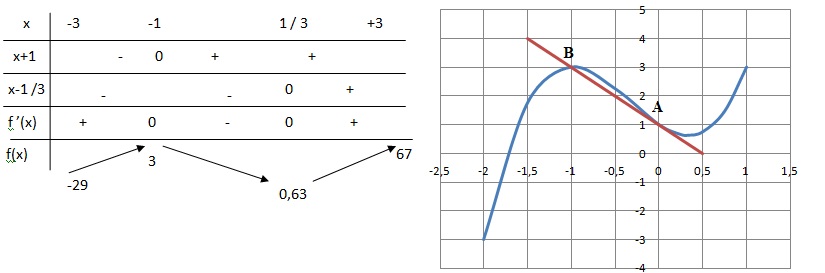
4.a. Vérifier qu’une équation de la tangente T à la courbe C au point A d’abscisse 0, est y=−2x+1.
Coefficient directeur de la tangente en A à la courbe C : f '(0) = -2.
A ( 0 ; 1) appartient à la tangente T : 1 = -2*0+b ; b = 1. y = -2x+1.
b. Montrer que cette tangente T passe par un point B de la courbe C, avec B distinct du point A.
En B : 2x3 + 2x2
– 2x + 1= -2x+1 ; 2x3 + 2x2
– =0 ; 2x2(x+1) = 0. Abscisse du point B : x= -1.
Ordonnée de B : yB = -2*(-1)+1) = 3.
|
|