Mathématiques,
QCM, fonction, suite, probabilités, géométrie.
enseignement de spécialité première générale.
|
.
.
|
|
Sujet 55
Exercice 1.
( 5 points ).
QCM ( aucune justification n'est demandée).
1. Une équation de la tangente à la courbe représentative de la fonction exponentielle au point d'abscisse 0 est :
a) y=x+1. Vrai.
b) y=ex
c) y=ex.
d) y=x-1.
f(x) = ex ; f 'x) = ex ; f '0) = 1.f(0) = 1.
Equation de la tangente : y = x+1.
2. La fonction 𝑓 définie sur ℝ par : 𝑓(𝑥)=𝑒−2𝑥+6 admet pour dérivée la fonction 𝑓 ′ définie sur ℝ par :
a) f '(x) = e-2x+6.
b) f '(x) = -2e-2x+6 Vrai.
c) f '(x) = -2xe-2x+6.
d) f '(x) = (-2x+6)e-2x+6.
On pose u = -2x+6 ; u' = -2 ; f(x) = eu ; f '(x) =u' eu = -2e-2x+6.
3. Dans le repère orthonormé (𝑂,𝑖⃗,𝑗⃗), le vecteur 𝐴𝐵⃗ représenté ci-dessous est égal à :
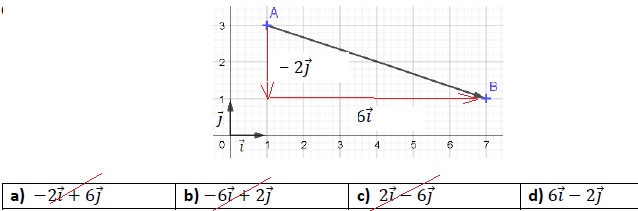
4.
On considère la fonction 𝑓 définie pour tout réel 𝑥 par
𝑓(𝑥)=sin𝑥−cos𝑥. Parmi les quatre propositions suivantes, une seule
est correcte. Laquelle ?
a). 𝑓 est une fonction paire.
b) 𝑓 est une fonction impaire.
c) f n'est ni paire ni impaire. Vrai.
d) f(0)=0.
sin x est impaire ; cos x est paire ; f(0) = sin(0) -cos(0) = 0-1=-1.
5. Dans le plan muni d’un repère, on considère la droite (d) d’équation : 5𝑥−2𝑦+8=0
La droite (d) a pour coefficient directeur :
a) le vecteur de coordonnées (2 ; 5 )
b) 2,5 vrai ; c) 0,4 ; d) -2.
2y=5x+8 ; y = 2,5x+4.
Sujet 56.
1. a) Si le discriminant d’un polynôme du second degré est strictement positif, alors ce polynôme admet 2 racines positives.
b) Si le discriminant d’un polynôme du second degré est strictement négatif, alors ce polynôme admet 2 racines négatives.
c) Si un polynôme du second degré est toujours strictement positif, alors ce polynôme n’admet pas de racine. Vrai.
d) Si le discriminant d’un polynôme du second degré est nul, alors ce polynôme admet le nombre 0 pour racine.
2. a) L’équation cos𝑥=− 0,5 admet 2 solutions dans l’intervalle ]−𝜋/2 ; 𝜋/2]. ( Dans cet intervalle cos x est positif ).
b) L’équation cos𝑥=− 0,5 admet 1 solution dans l’intervalle [0 ; 𝜋[. Vrai.
c) L’équation sin𝑥=− 0,5 admet 1 solution dans l’intervalle [0 ; 𝜋[. ( Dans cet intervalle sin x est positif ).
d) L’équation sin𝑥=− -0,5 admet 2 solutions dans l’intervalle ]−𝜋/2 ; 𝜋/2].
3.
La courbe représentative d’une fonction 𝑓, définie et dérivable sur
l’ensemble des nombres réels, est donnée ci-dessous avec ses tangentes,
aux points A et B d’abscisses respectives 2 et 4. On note 𝑓’ la
fonction dérivée de 𝑓.
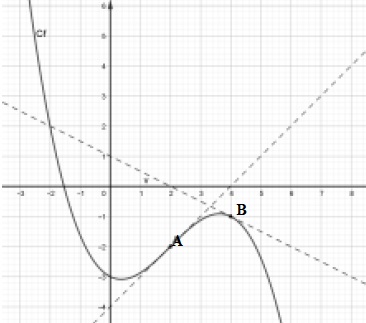
A. f(0) =1 . ( f(0) = -3).
B. f ' (2)=1.( coefficient directeur de la tangente en A) Vrai.
C. f '(2)=-2 ( coefficient directeur de la tangente en B = -0,5)
D. f (4) = 0,5. ( f(4) = -1)
4. On considère la fonction 𝑔 définie sur l’ensemble des nombres réels R par : 𝑔(𝑥)=𝑥3−0,0012𝑥+1.
a) 𝑔 est strictement croissante sur R.
b) 𝑔 est croissante sur R.
c) 𝑔 est constante sur l’intervalle [− 0,02 ;0,02].
d) 𝑔 est décroissante sur l’intervalle [− 0,02 ;0,02]. Vrai.
g'(x) =3x2-0,0012.
g'(x) = 0 si x = ± racine carrée (0,0012 / 3 )soit ±0,02.
g'(x) < 0 sur [− 0,02 ;0,02] ; g(x) est décroissante sur l’intervalle [− 0,02 ;0,02].
5. a) L’équation (e𝑥)2=1 admet deux solutions dans R.
b) L’ensemble de définition de la fonction exponentielle est ]0 ; + ∞[.
c) La fonction dérivée de la fonction 𝑥 ↦ e−𝑥 est la fonction 𝑥 ↦ e−𝑥 . ( - e-x)
d) L’ensemble de définition de la fonction exponentielle est R.
Réponse D.
|
|
Exercice 2. ( 5
points) Sujet 55. Un
fermier souhaite réaliser un enclos rectangulaire pour des poules et
des poussins, adossé à un mur de sa ferme afin d’économiser du
grillage. Ainsi, il ne grillagera que 3 côtés de son enclos. Il possède
28 mètres de grillage. Il souhaite construire un enclos d’aire maximale.
On appelle 𝑥 la longueur du côté de l’enclos perpendiculaire au mur.
On appelle 𝐴 la fonction qui à un nombre 𝑥 associe 𝐴(𝑥) l’aire de
l’enclos. La fonction 𝐴 est ainsi définie sur l’intervalle [0 ;14].1.
a. Vérifier que l’aire 𝐴(𝑥)=−2𝑥²+28𝑥.
28 = 2 largeurs + une longueur ; longueur =28-2 largeurs = 28-2x.
A(x) = largeur fois longueur du rectangle = x (28-2x) =-2x2+28x.
b. Montrer que la forme canonique de 𝐴(𝑥) est −2(𝑥−7)2+98.
A(x) = -2(x2-14x) =-2(x2-14x+49-49) =-2(x-7)2+98.
2. Quatre courbes ont été tracées sur le graphique ci-dessous. Identifier celle qui représente la fonction 𝐴.
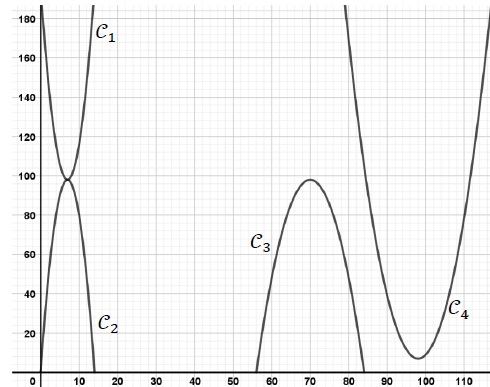
Le coefficient a =-2 étant négatif, la parabole possède un maximum.
A(0) = A(14)=0, donc courbe C2.
3. Dresser le tableau de variation de la fonction 𝐴.
4. Pour quelle valeur de x l’aire de l’enclos est-elle maximale ? Donner la valeur de cette aire.
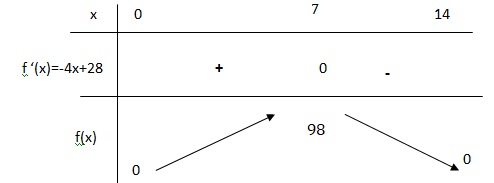
L'aire est maximale pour x = 7. L'aire maximale vaut 98 m2.
Sujet 56.
Lorsqu’il s’entraine au tennis, Roger utilise un lance balle.
Cette machine lance les balles soit sur le coup droit soit sur le revers du joueur.
On la remplit de balles et on la programme de la façon suivante : deux
tiers des balles seront lancées sur le coup droit du joueur, le reste
sur son revers.
On s’intéresse à la réussite des frappes de Roger pendant une séance d’entraînement.
On note 𝐷 l'événement : « le joueur reçoit la balle sur son coup droit ».
Roger réussit 9 / 10 de ses coups droits et 75 % de ses revers.
On note 𝑆 l'événement : « La frappe de Roger est un succès ».
1. Donner p( non 𝐷).
p(non D) = 1 /3.
2. Compléter l’arbre pondéré représentant la situation.
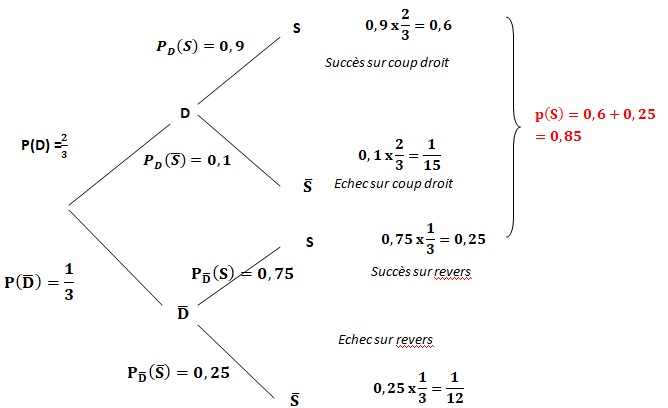
3. Calculer p(non 𝐷∩ 𝑆). Interpréter ce résultat dans le contexte de l’exercice.
p(non 𝐷∩ 𝑆)= 0,75 x 1 /3 = 0,25.
La probabilité que la balle reçue sur le revers et soit un succés est égale à 0,25.
4. Montrer que la probabilité que la frappe de Roger soit un succès est égale à 0,85.
p(S) = 0,9 *2 /3 +0,75 *1 /3 = 0,6 +0,25 = 0,85.
5. Sachant que la
frappe que vient de réaliser Roger est un succès, calculer la
probabilité que ce soit sur un revers. Arrondir le résultat au centième.
PS(non D) = P(S n non D) / P(S) = 0,25 /0,85 ~0,29.
|
|
Exercice 3. ( 5 points).
Sujet 55.
Le plan est muni d’un repère orthonormé.
On considère les points 𝐴, 𝐵 et 𝐶 de coordonnées : 𝐴 (7 ; −2), 𝐵 (7 ; 4) et 𝐶 (1 ; 1).
1. Montrer que 𝑦=1 est une équation de la droite (𝑑1) passant par 𝐶 et perpendiculaire à (𝐴𝐵).
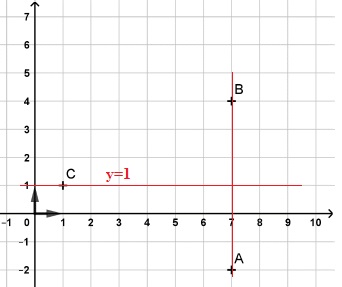
Equation cartésienne de la droite (AB) : x - 7 =0.
Equation cartésienne de la droite d1, perpendiculaire à (AB) :y+d=0.
C(1 ; 1) appartient à cette droite d1 : 1+d=0 ; d=-1.
2. Que représente cette droite pour le triangle 𝐴𝐵𝐶 ?
Cette droite est la hauteur du triangle ABC, issue de C.
3. Donner une équation de la droite (𝑑2), hauteur du triangle 𝐴𝐵𝐶 issue du sommet B.
Coordonnées du vecteur AC : xC-xA ; yC-yA soit ( -6 ;3).
Equation cartsienne de la droite d2, perpendiculaire à (AC) : -6x+3y+b=0.
B( 7 ; 4) appartient à d2 : -6*7+3*4+b=0 ; b = 30.
-6x+3y+30=0 ou encore -2x+y+10=0.
4. On appelle 𝐻 le point d’intersection des droites (𝑑1) et (𝑑2).
Donner en justifiant la valeur du produit scalaire 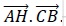
H est l'orthocentre du triangle ABC.
AH est la hauteur du triangle ABC, issue de A.
AH est perpendiculaire à BC et le produit scalaire 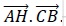 est nul. est nul.
Sujet 56.
Le
plan est rapporté à un repère orthonormé (O; 𝑖⃗ ,𝑗⃗). On considère le
triangle OAB où O est l’origine du repère, A le point de coordonnées (8
; 0) et B celui de coordonnées (0 ; 6).
On considère le point E, milieu du segment [AB].
La figure est donnée, elle sera complétée au fur et à mesure et sera rendue avec la copie.
On rappelle que dans un triangle, la médiane issue d’un sommet est la
droite passant par ce sommet et par le milieu du côté opposé et que le
centre de gravité d’un triangle est le point de concours de ses 3
médianes.
1. Calculer les 2 produits scalaires suivants :
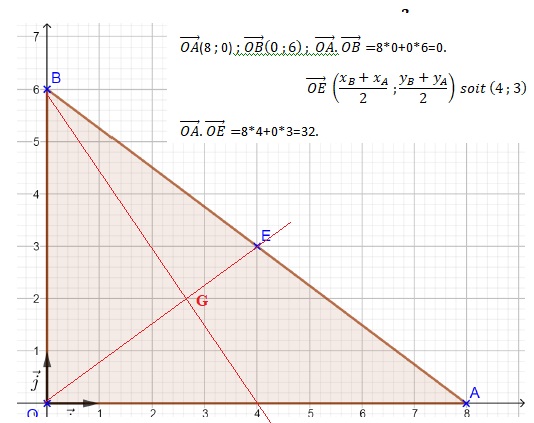
2.
a) Justifier que
l’équation 1,5x + y – 6 = 0 est une équation cartésienne de la médiane
issue du point B dans le triangle OAB. Tracer cette médiane sur la
figure.
Equation cartésienne de cette médiane : ax +by +c=0.
Le point de coordonnées (4 ; 0) appartient à cette médiane : 4a+c=0. (1)
Le point B de coordonnées (0 ; 6) appartient à cette médiane : 6b+c=0. (2)
(1)-(2) donne : 4a = 6b soit a = 1,5 b.
1,5 bx +by -6b=0 soit 1,5x + y – 6 = 0.
b) Déterminer une équation de la médiane issue de O dans le triangle OAB.
Equation cartésienne de cette médiane : ax +by +c=0.
O appartient à cette médiane : c = 0.
E appartient à cette médiane :4a+3b=0 soit a = -0,75 b.
-0,75 b x+by=0 soit -0,75x+y=0 ou y = 0,75 x.
c) Déterminer les coordonnées du point G, centre de gravité du triangle OAB. Placer le point G sur la figure.
1,5xG + yG – 6 = 0 et yG = 0,75 xG.
1,5xG + 0,75xG – 6 = 0 ; xG = 8 / 3 et yG =2.
|
|
Exercice 4. ( 5 points) Sujet 55. La
bibliothèque municipale étant devenue trop petite, une commune a décidé
d’ouvrir une médiathèque qui pourra contenir 100 000 ouvrages au total.
Pour l’ouverture prévue le 1er janvier 2020, la médiathèque dispose du
stock de 35 000 ouvrages de l’ancienne bibliothèque, augmenté de 7 000
ouvrages supplémentaires neufs offerts par la commune.
Partie A.
Chaque année, le bibliothécaire est chargée de supprimer 5% des
ouvrages, trop vieux ou abîmés, et d’acheter 6 000 ouvrages neufs.
On appelle 𝑢𝑛 le nombre, en milliers, d’ouvrages disponibles le 1er janvier de l’année (2020+𝑛).
On donne 𝑢0 = 42.
1. Justifier que, pour tout entier naturel 𝑛, on a 𝑢𝑛+1 = 𝑢𝑛×0,95+6.
Chaque année, on supprime 5 % des ouvrages et on en achète 6000.
1-0,05 = 0,95 ; un+1 = 0,95 un +6.
2. On propose ci-dessous un programme en langage Python :
def suite(n)
u=42
for i in range(n)
u = 0,95*u+6
return u
Expliquer ce que permet de déterminer ce programme.
Ce programme donne le nombre d'ouvrage en l'an 2019 +n, c'est à dire la valeur de un.
Partie B.
La commune doit finalement revoir ses dépenses à la baisse, elle ne
pourra financer que 4 000 nouveaux ouvrages par an au lieu des 6 000
prévus.
On appelle 𝑣𝑛 le nombre, en milliers, d’ouvrages disponibles le 1er janvier de l’année (2020+𝑛).
1. On admet que 𝑣𝑛+1 = 0,95×𝑣𝑛+4 pour tout entier naturel 𝑛≥0 avec 𝑣0 = 42.
On considère la suite (𝑤𝑛) définie, pour tout entier naturel 𝑛, par 𝑤𝑛= 𝑣𝑛−80.
a. Montrer que (𝑤𝑛) est une suite géométrique de raison 𝑞 = 0,95 et préciser son premier terme 𝑤0.
𝑤𝑛+1= 𝑣𝑛+1−80 =0,95×𝑣𝑛+4-80=0,95×𝑣𝑛-76 =0,95( vn -80)=0,95 wn.
wn est une suite géométrique de raison 0,95 et de premier terme 42-80 = -38.
b. En déduire l’expression de 𝑤𝑛 puis de 𝑣𝑛 en fonction de 𝑛.
wn=-38 * 0,95n ; vn = wn +80 = -38 * 0,95n +80.
2. On donne ci-dessous un programme en langage Python.
def objet(A)
v=42
n=0
while v < A:
v=0,95*v +4
n=n+1
return n
L’appel à la fonction objet(70) renvoie 27. Interpréter ce résultat dans le contexte de l’exercice.
en 2020+27 soit en 2047, la médiatèque comptera plus de 70 mille ouvrages.
|
Sujet 56.
En 2016, a été lancée une plateforme de streaming par abonnement.
Le tableau suivant donne le nombre d’abonnés (en million) au 31 décembre de chaque année de 2016 jusqu’en 2019.
Rang de l'année
|
1
|
2
|
3
|
4
|
31 décembre de l'année
|
2016
|
2017
|
2018
|
2019
|
Nombre d'abonnés ( millions)
|
12
|
13,7
|
15,8
|
18,2
|
Les responsables de cette plateforme étudient l’évolution du nombre d’abonnés afin d’adapter leurs investissements.
1. Quelle a été en pourcentage l’évolution du nombre d’abonnés entre 2016 et 2017 ?
(13,7-12) / 12 x100 ~14,2 %.
2. Expliquer pourquoi le taux moyen d’évolution par an entre 2016 et 2019, arrondi au centième, est de 14,89%.
12 (1 +14,89 /100)3 ~18,2.
3.
On considère que le nombre d’abonnés a augmenté de 15% par an à partir
de 2016. On décide de modéliser ce nombre d’abonnés (en millions) par
une suite de premier terme 12.
Préciser la nature de cette suite et sa raison.
Suite géométrique de raison1+0,15 = 1,15 et de premier terme 12.
4. Quel sera selon ce modèle, le nombre d’abonnés au 31 décembre 2020 ?
u4=12 x1,154 ~20,99 millions.
5. Pour déterminer
en quelle année, selon ce modèle, sera obtenu l’objectif de 40 millions
d’abonnés, on a défini en langage Python la fonction Seuil ci
dessous. Compléter les instructions afin que ce programme fournisse l’année où cet objectif sera atteint.
def Seuil():
n=2016
A=12
while A < 40 :
A= A*1,15
n=n+1
return n
|
|