Spécialité
Mathématiques, classe de première 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
.
|
|
Exercice 1. QCM.
1. Soit f la fonction définie sur R par f(x) =x2+x+1.
Sa fonction dérivée f '(x) est donnée par :
f '(x) = x+1 ; f '(x) =2x+1 vrai ; f '(x) =2x ; f '(x) = 2x2+x.
2.La somme 1 +2+22 +23 +...+210 est égale à :
210-1 ; 210 ; 211-1 vrai ; 211.
Somme des onze premiers termes d'une suite géométrique de premier terme 1 et de raison 2.
S = 1 *(211-1) /(2-1) = 211-1.
3. On considère l'équation x2+2x-8=0. On note S la somme de ces racines et P leur produit.
Quelle affirmation est vraie ?
S=2 et P = -8 ; S = -2 et P =-8 vrai ; S =-2 et P = 8 ; S = 2 et P = 8.
S = -b / a = -2 /1 = -2 ; P = c /a = -8 /1 = -8.
4. On désigne par C le cercle trigonométrique. Soit x un réel strictement positif et M le point C associé au réel x.
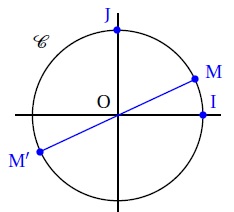
Alors le point M', symétrique de M par rapport à O, est associé au réel :
-x ; p+x vrai ; p-x ; -p-x.
M et M' étant diamétralement opposés, la différence des réles qui leurs sont associés est égale à p.
5. Parmi les égalités suivantes, laquelle est vraie pour tout réel x ?
cos(x+2p) = cos (x) vrai.
sin(-x) = sin (x) ; cos(-x) = - cos(x) ; cos2(x) + sin2(x) = 2.
Exercice 2.
Soit f la fonction définie sur R par f(x) = (2x+1)ex. Sur le graphique, sont représentées la courbe C représentative de la fonction f, et la droite T, tangente à C en x = 0.
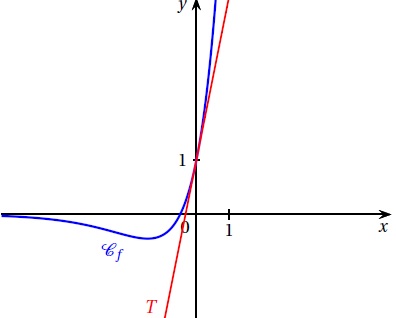
1. Déterminer les coordonnées d'éventuels points d'intersection de la courbe C avec l'axe des abscisses.
Il faut résoudre l'équation f(x) = (2x+1)ex =0.
ex est strictement positif.
2x+1=0 soit x = -½.
2. Montrer que f '(x) = (2x+3)ex.
On pose u = 2x+1 et v = ex ; u' = 2 ; v' = ex.
u'v +v'u = 2ex +(2x+1)ex = (2x+3)ex.
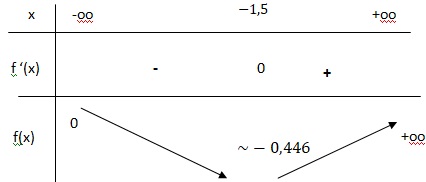
3. Dresser le tableau de signe de f '(x) puis préciser les variations de f sur R..
ex >0, f '(x) a le signe de 2x+3.
4. a. Déterminer l'équation réduite de la tangente T.
Coefficient directeur de la tangente T: f '(0) =3.
Equation de T : y = 3x+b.
Le point de coordonnées (0 ; f(0) = 1) appartient à T : 1 = b ;
Equation réduite de T : y = 3x+1.
4.b. Justifier graphiquement, que pour tout réel x, on a : (2x+1)ex > 3x+1.
D'après le graphique, la courbe C d'équation (2x+1)ex est située au dessus de la tangente T d'équation y = 3x+1, sau f au point de tangence.
Donc (2x+1)ex > 3x+1.
|
Exercice 3.
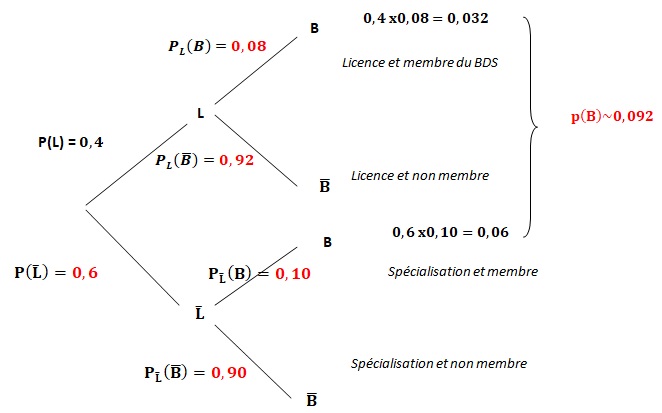
Dans une école, 40 % des étudiants sont dans le cycle licence et 60 % dans le cycle de spécialisation.
Parmi les étudiants de licence, 8 % sont dans le BDS ( bureau des sports).
Parmi les étudiants de spécialisation, 10 % sont membres du BDS.
On considère un étudiant de cette école, choisi au hasard, et les événements suivants :
L : l'étudiant est en licence.
B : l'étudiant est membre du BDS.
Partie A.
1. Compléter l'arbre pondéré représentant la situation.
2. Calculer la probabilité que l'étudiant choisi soit en licence et membre du BDS.
3. Montrer que P(B) = 0,092.
Partie B.
Le BDS décide d'organiser une randonnée. le prix est de 60 € pour les
étudiants ne faisant pas partie du BDS et 20 € pour les membres du BDS.
On désigne par X la variable aléatoire donnant la somme à payer pour un
étudiant qui désire faire la randonnée.
1. Quelles sont les valeurs prises par X.
20 € et 60 €.3. Donner la loi de probabilité de X et calculer l'espérance de X.
Valeurs de X
|
20
|
60
|
P(X)
|
0,092
|
1-0,092=0,908
|
Espérance E= 20 x0,092 +60 x0,908 =1,84 +54,48 =56,32 €.
Exercice 4.
Bob s'est fixé l'objectif de participer à un marathon. Il programme sa préparation :
20 km lors du premier entraînement puis à chaque entraînement suivant, il augmente sa distance de 5 %.
La distance parcourue est modélisée par une suite (dn) où le nombre dn désigne la distance parcourue en km, lors de son n-ième entraînement. Ainsi d1 = 20.
1. Calculer d2 et vérifier que d3 = 22,05.
d2 = d1 +d1 x0,05 = 1,05 d1 = 1,05 x20 =21.
d3 = 1,05 d2 = 21 x1,05 =22,05.
2. Exprimer dn+1 en fonction de dn.
dn+1 = 1,05 dn.
3. Justifier que pour tout entier naturel n > 1, dn = 20 x1,05n-1.
(dn) est une suite géométrique de premier terme d1=20 et de raison 1,05.
dn = 20 x1,05n-1.
4. Quelle distance, arrondie à 1 m près, va parcourir Bob lors de son 10ème entraînement ?
5. La courbe C et le droite D ont-elles un point commun ? Justifier.
d10 =20 x1,059 =31,027 km.
6.
La distance à parcourir lors d'un marathon est de 42,195 km. Bob
estime qu'il sera prêt s'il parvient à courir au moins 43 km lors de
ces entraînenemts. Compléter le script suivant dont la valeur n, après
excécution du script, est le nombre minimal d'entraînements permettant
à Bob d'être prêt.
n=1
d=20
while d < 43
n =n+1
d=1,05*d
|
|



