Physique
chimie, le superamas Laniakea, smarphone et photgraphie, .
E3C : enseignement de spécialité première générale.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
Le
superamas Laniakea.
Partie 1 : différents
télescopes pour différents types de photons de lumière.
Pour identifier et mesurer les vitesses des galaxies de Laniakea, les
cosmographes utilisent des télescopes qui peuvent recueillir les
photons émis par ces galaxies lointaines. Les photons de différentes
longueurs d’ondes se propagent à travers le cosmos, à la vitesse de la
lumière dans le vide. Le télescope Canada-France-Hawaï (TCFH) et son
miroir de 3,60 m de diamètre est situé au sommet du Mauna Kea à Hawaï à
une altitude de 4 204 m. C’est un télescope optique qui est sensible
aux lumières visible et infrarouge du cosmos. Lien
web : www.rncan.gc.ca
1.1.À partir de la lecture du
document ci-dessus, le TCFH peut-il capter des photons d’énergie de
haute ou basse fréquence ?
Les photons du domaine visible ou infrarouge sont de l'ordre de 1014
Hz, domaine des hautes fréquences..
1.2. Quel est
l’ordre de grandeur de la longueur d’onde des photons que peut capter
le TCFH ? Justifier votre réponse.
l =c
/ f = 3 108 / 1014 = 3 10-6 m ( de
l'ordre du micromètre ).
Le Green Bank Télescope (GBT) (États-Unis) est un radiotélescope de 110
m de diamètre qui permet de capter des photons invisibles pour nos
yeux. Le rayonnement radio s’étend du millimètre au kilomètre. À titre
d’exemple, le GBT est sensible aux ondes de longueur d’onde de 10 cm,
comme celles utilisées pour les téléphones portables. C’est pour cette
raison qu’il est interdit d’utiliser un téléphone portable (ou même un
four micro-onde) dans un environnement proche du GBT.
1.3.Le GBT peut-il
capter des photons dont la longueur d’onde est plus courte ou plus
longue que le TCFH ? Justifier votre réponse.
Le TCFH est sensible aux ondes de longueur
d’onde de l'ordre de 1 µm. Le
GBT est sensible aux ondes de longueur d’onde de 10 cm, donc de
longueur d'onde plus longue que le TCFH.
1.4.Quelle est la valeur de la
fréquence des ondes radio utilisées par les téléphones portables ?
Les fréquences sont situées entre 450 et 2700 MHz. ( longueur d'onde
comprises entre 0,66 m et 1,1 mm )
1.5. Expliquer
pourquoi on ne peut pas utiliser un téléphone portable dans un
environnement proche du GBT.
Le GBT est
sensible aux ondes de longueur d’onde de 10 cm, comme celles utilisées
pour les téléphones portables.
Partie
2 : énergie d’un photon galactique.
2.1.
Calculer la valeur de l’énergie d’un photon de longueur d’onde 10 cm,
en Joule, puis en électronvolt (eV).
E = hc / l
= 6,63 10-34 x 3 108 / 0,1 =1,989 10-24
J soit 1,989 10-24 / (1,6 10-19) =1,24 10-5
eV.
2.2. Pourquoi le télescope TCFH ne
peut-il pas capter ce photon ? Justifier votre réponse.
C’est un télescope
optique qui est sensible aux lumières visible et infrarouge. Les
énergies des photons sont de l'ordre de :
6,63 10-34
x 3 108 / 10-6 ~1,989 10-19 J soit 1,989 10-19
/ (1,6 10-19) =1,2 eV.
Partie 3
: la mesure de la vitesse de rotation des galaxies à partir des photons
émis par l’hydrogène
L’exploitation des données
recueillies par le GBT permet de mesurer
la valeur de la vitesse de rotation sur elle-même d’une galaxie spirale. Plus précisément, on peut
mesurer la vitesse de rotation des
nuages de gaz d’hydrogène présents à
la périphérie de la galaxie. En effet, ces nuages de gaz d’hydrogène émettent de la lumière dont la
longueur d’onde varie avec la
vitesse de rotation de la galaxie spirale. Plus les galaxies tournent vite, plus elles sont
riches en étoiles ; elles émettent
alors davantage de lumière.
On considère dans un premier
temps un photon émis par un atome
d’hydrogène qui passe du niveau d’énergie
n = 3 au niveau d’énergie n = 2.
3.1.
Quelle est la valeur de la longueur d’onde du photon émis ?
Energie du niveau 3 : -1,51 eV ; énergie du niveau 2 : -3,39 eV.
Différence d'énergie : 3,39 -1,51 = 1,88 eV soit 1,88 x1,6 10-19
~3,0 10-19 J.
Longueur d'onde du photon émis : 6,63 10-34 x3 108
/ (3,0 10-19) =6,6 10-7 m = 660 nm ( domaine
visible)
3.2. À quel domaine du spectre
électromagnétique appartient cette
longueur d’onde ? Justifier.
660 nm est compris entre 400 nm et 800 nm, limites du domaine visible.
3.3. Ce photon peut-il être capté
par le GBT ? Justifier.
Non, le GBT peut capter seulement des photons dont les longueurs d'onde
s'étendent du mm au km.
En fait, la mesure de la
luminosité d’une galaxie lointaine
s’effectue à partir de la raie d’émission de longueur d’onde 21 cm de l’atome d’hydrogène.
3.4.
Calculer la valeur de la variation d’énergie à laquelle correspond cette émission ?
6,63 10-34 x3 108 / 0,21
=9,5 10-25 J.
|
|
Smartphone
et photographie.
Les smartphones sont de plus en plus performants et tendent à
concurrencer les appareils photographiques numériques compacts. Dans un
appareil photographique simple la mise au point est faite en déplaçant
une lentille. La finesse des smartphones ne permet pas de déplacer
la lentille et la mise au point est réalisée en déformant une goutte
liquide servant de lentille pour modifier la valeur de sa distance
focale.
La valeur de la distance focale de cette lentille liquide est modifiée
en fonction de la position de l’objet à photographier.
Dans cet exercice, on s’intéresse à la perception des couleurs d’une
figurine puis à la manière dont le système optique du téléphone modifie
sa distance focale pour photographier la figurine située à 30,0 cm de
la lentille.
1. Couleurs de la
photographie.
La figurine possède des chaussures bleues et porte une veste de couleur
jaune-orangé. Elle est éclairée en lumière blanche.
1.1. La couleur de
la veste de la figurine est perçue jaune-orangée lorsqu’elle est
éclairée en lumière blanche, en déduire la couleur absorbée. Justifier
en expliquant le principe de la synthèse de lumière impliqué dans ce
phénomène.
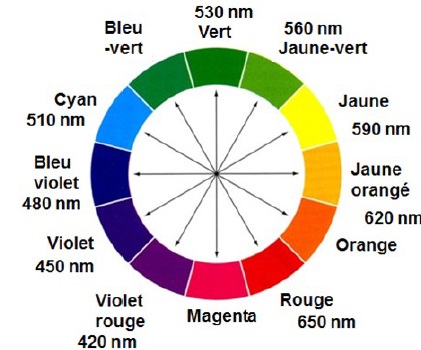
Les flèches correspondent à des couleurs complémentaires qui sont donc
placées face à face.
Synthèse additive.
La veste éclairée en lumière blanche absorbe la couleur complémentaire
du jaune orangé, c'est à dire le bleu violet.
1.2. Après avoir
pris la photographie, un filtre de couleur bleu-violet est appliqué sur
l’image.
1.2.1. Donner la
couleur perçue par l’oeil de l’observateur quand il regarde la veste de
la figurine à travers ce filtre. Justifier.
Ce filtre laisse
passer la lumière bleu-violet et absorbe le jaune-orangé. La veste
paraît grise ou noire.
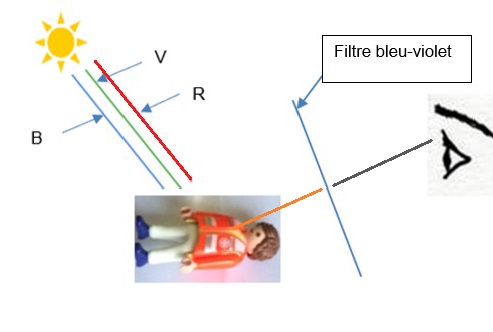
1.2.2. Compléter le schéma
illustrant votreréponse à la question 1.2.1 et pour laquelle la lumière
blanche est modélisée par les
rayonnements R (rouge), V (vert) et B (bleu).
2. Distance focale de la
lentille liquide.
On cherche à évaluer la valeur de la distance focale f’ de la lentille
d’un smartphone qu’on assimile à une lentille mince convergente (L) de
centre optique O. La figurine servant d’objet A B est placée à 30,0 cm
devant la lentille. L’image A' B' est recueillie sur un capteur
derrière la lentille. Par la suite cette image A' B' est agrandie afin
d’obtenir une autre image A'' B'' visible sur l’écran du smartphone.
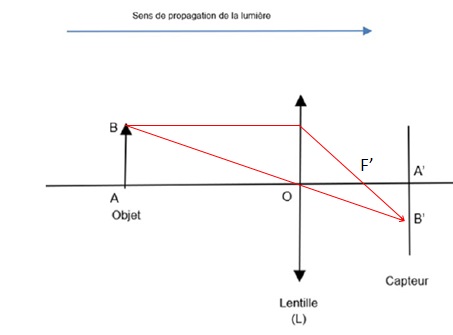
2.3.1. Sans souci
d’échelle compléter le schéma, en plaçant les rayons lumineux issus de
B et permettant de positionner précisément le point B’
(image de B à travers la lentille), le foyer image F ’ ainsi que la
distance focale f’ = O ´F ’.
2.2. Résultats
expérimentaux
Le smartphone utilisé possède un capteur de format « 1/2.5“ ».
Dimensions : longueur 5,76 mm ; largeur 4,29 mm.
L’écran du smartphone a une longueur de 10,5 cm. La figurine,
photographiée dans le sens de la longueur du smartphone, a une taille
de 2,0 cm sur cet écran. Lors de l’agrandissement capteur-écran les
proportions sont conservées.
2.2.1. À l’aide des
résultats expérimentaux ci-dessus, de la conservation des proportions
capteur-écran et des données sur les capteurs, vérifier par calcul que
la taille de l’image est A' B' = - 0,11 cm sur le capteur.
L'image A'B' est inversée par rapport à l'objet, d'où le signe négatif.
Rapport des proportions capteur - écran : 0,576 / 10,5 =5,49 10-2.
Taille de l'image sur le capteur : 2,0 x 5,49 10-2 ~0,11 cm.
2.2.2. En utilisant
les données ci-dessous, les réponses aux questions précédentes, et
sachant que la taille réelle de la figurine est de 7,5 cm déterminer à
l’aide de calculs la valeur de la distance focale f ’ de ce smartphone
lorsqu’il donne une image nette de la figurine placée à 30,0 cm de la
lentille.
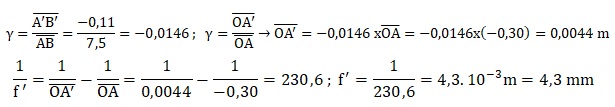
|
3.
Transformer son smartphone en « microscope ».
En déposant une goutte d’eau sur l’objectif photographique de son
smartphone on peut le transformer en « superloupe ». L’image est alors
agrandie comme avec un petit microscope.
Le rayon de la goutte déposée est Rc = 1,0 mm. La goutte est
assimilable à une lentille de distance focale f ’eau dont la
valeur peut se calculer à l’aide des informations suivantes
(n = 1,33 est l’indice de l’eau).
La distance focale équivalente f ’ équivalente,
correspondant à l’association de la goutte d’eau et de la lentille, se
calcule à l’aide de la relation suivante :
1 / f 'équivalente = 1 / f 'eau + 1 / f 'smarphone
et 1 / f 'eau = (n-1) / Rc avec n = 1,33.
Montrer par des calculs, en utilisant les informations ci-dessus, que
le facteur d’agrandissement d’une image prise avec la goutte sur le
smartphone est de l’ordre de ×15 ( f ' équivalente =
1,77 mm) si on considère que la
valeur de la distance focale de la lentille du smartphone est f ’ smartphone
= 4,2 mm.
1
/ f 'eau = (n-1) / Rc = (1,33-1) / 0,001 =3,3 102.
1 / f 'équivalente
= 3,3 102 +1 / (4,2 10-3) =568 ; f 'équivalente =1 / 568 ~1,76 10-3
m = 1,76 mm.
|
|
|