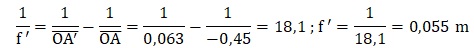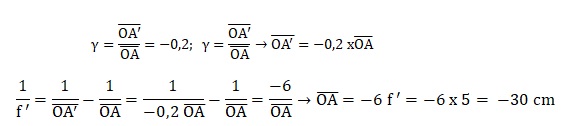Physique
chimie, synthon d'un antihypertenseur, la photographie,
l'exploit d'Alan Eustace.
E3C : enseignement de spécialité première générale.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
.
|
|
Synthon
d'un antihypertenseur.
Pour
synthétiser une molécule complexe les chimistes la « coupe »
fictivement en plusieurs fragments appelés « synthons ». Le choix des
synthons se fait de telle sorte qu’ils soient fabriqués en un minimum
d’étapes avec de bons rendements. Ces synthons réagiront ensuite entre
eux pour conduire à la molécule souhaitée.
Dans le cas de la synthèse de l’irbésartan, une équipe de chimiste a
envisagé la fabrication des deux synthons ci-dessous (synthons 1 et 2) :
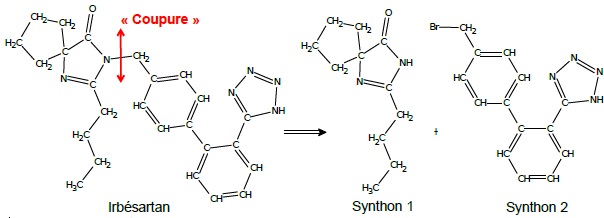
La synthèse du synthon 1 se fait en trois étapes à partir de la
molécule de cyclopentanone. Ce sujet porte sur l’étape 1 de cette
synthèse multi-étapes, celle permettant d’obtenir le composé A.
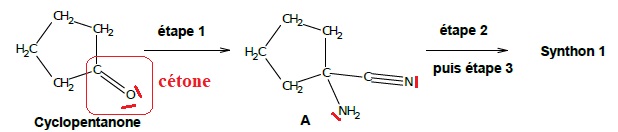
Protocole expérimental de l’étape 1 :
1- Dans un ballon de 250 mL, introduire 5,2 g (80 mmol) de cyanure de
potassium solide, 8 mL d’eau et un barreau aimanté. Mettre le tout
au-dessus d’un agitateur magnétique et agiter jusqu’à dissolution
complète.
2- Introduire successivement 20 mL d’une solution aqueuse d’ammoniac de
concentration en quantité de matière d’ammoniac 10,8 mol.L- 1,
puis 6,3 mL de cyclopentanone dissous dans 8 mL de méthanol.
3- Surmonter le ballon d’un réfrigérant, agiter et chauffer le mélange
durant 45 minutes à 60 °C.
4- Laisser refroidir tout en continuant à agiter durant 45 minutes.
5- Verser le mélange dans une ampoule à décanter et ajouter 50 mL de
dichlorométhane. Séparer les phases.
6- Extraire la phase aqueuse avec trois fois 25 mL de dichlorométhane.
7- Rassembler les phases organiques et les sécher avec du sulfate de
magnésium anhydre MgSO4 (s). Filtrer et récupérer la phase
organique.
8- Le solvant organique est évaporé et on obtient alors 7,1 g d’une
huile incolore : le composé A.
1. À propos des réactifs
et produits.
1.1. Définir un
composé organique.
Un composé organique est composé de carbone et d'un petit nombre
d'éléments, hydrogène, oxygène, azote, halogènes, soufre.
1.2. Recopier la
molécule de cyclopentanone et la molécule A sur la copie et y ajouter
tous les doublets non liants de la molécule. Justifier la démarche.
L'atome d'oxygène compte 6 électrons de valence, dont 2 sont engagés
dans la liaison C=0 : il reste 4 électrons ( 2 doublets non liants).
L'atome
d'azote compte 5 électrons de valence, dont 3 sont engagés dans des
liaisons : il reste 2 électrons ( un doublet non liant).
1.3. Entourer le groupe
caractéristique présent sur la molécule de cyclopentanone et préciser
le nom de la famille de composés associée. Voir ci-dessus.
2. Analyse du protocole
Deux solvants sont mélangés lors de cette synthèse, l’eau et le
méthanol, dont le mélange est homogène.
2.1. Représenter le
schéma de Lewis de la molécule d’eau, puis celui de la molécule de
méthanol de formule brute CH4O.
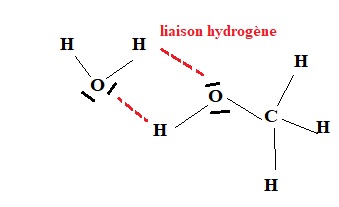
2.2. Donner le nom
de l’interaction prépondérante entre l’eau et le méthanol qui permet
d’expliquer la présence d’une seule phase dans le milieu réactionnel.
Justifier à l’aide d’un schéma.
2.3. Citer le nom
du montage utilisé lors du chauffage. Donner son intérêt.
Le chauffage à reflux permet d'accélérer la réaction ( la température
est un facteur cinétique) tout en évitant les pertes de matière. Les
vapeurs se condensent dans le réfrigérant et retombent dans le milieu
réactionnel.
2.4. Donner le nom
de l’opération effectuée lors des étapes 5 et 6 du protocole de
synthèse.
Extraction.
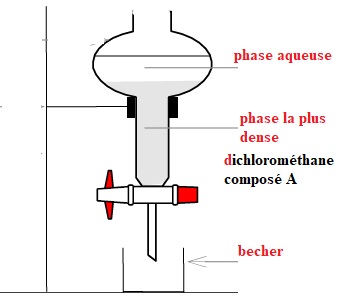
2.5. Compléter le
schéma correspondant à la fin de l’opération 5. Préciser la nature des
phases sur le schéma en justifiant la réponse
et indiquer dans quelle phase se trouve le composé A.
2.6. Donner le nom
de l’opération 7 et préciser le rôle du sulfate de magnésium anhydre
ajouté à la phase organique lors de cette étape.
On élimine les traces d'eau, le sulfate de magnésium est un déhydratant.
3. Rendement de la synthèse.
L’équation de la réaction modélisant la transformation associée à
l’étape 1 est la suivante :
C5H8O(l) + CN-( aq)+ NH3
(aq) → C6H10N2 + HO-( aq)
3.1. Calculer les
quantités de matière d’ammoniac et de cyclopentanone introduites
initialement dans le milieu réactionnel.
Cyclopentanone : 6,3 mL ; masse volumique 950 g / L soit 0,95 g / mL.
Masse : 6,3 x0,95 =5,985 g.
n = 5,985 / M(cyclopentanone ) = 5,985 / 84,1 =0,0712 mol.
Ammoniac : 20 mL à 10,8 mol /L.
Quantité de matière : 0,020 x10,8 =0,216 mol ( excès).
3.2. En déduire la
valeur de l’avancement maximal de la réaction xmax.
xmax ~0,071 mol.
3.3. Définir le
rendement de la synthèse et le calculer en admettant que l’huile
incolore obtenue correspond au composé A pur.
On peut espérer obtenir au mieux 0,071 mol de A.
M(A) = 110,2 g / mol ; masse théorique : 0,071 x110,2 =7,8 g.
Rendement : masse réelle / masse théorique =7,1 / 7,8 = 0,91 ( 91 %).
|
|
La
photographie.
1. Gros plan sur un martin
pêcheur.
Un photographe dit avoir pris la photographie en milieu naturel, avec
un objectif dont la distance focale peut varier de 28 mm à 100 mm. Il
ne précise pas la distance focale utilisée pour cette image. L’oiseau
était situé à 45 cm du centre optique de l’objectif et le capteur à 63
mm de ce centre optique. La taille d’un martin pêcheur adulte est de
l’ordre de 16 cm.
1.1. Distance focale de
l’objectif.
1.1.1. Réaliser une
construction graphique, à l’échelle ¼, pour déterminer la valeur de la
distance focale de l’objectif lors de la
prise de cette photo.
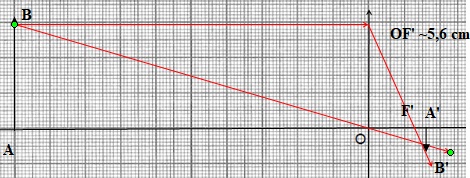
1.1.2. Retrouver
cette valeur par un calcul.
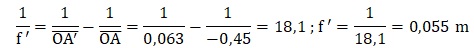
1.2. Format du capteur.
1.2.1. Calculer le
grandissement g,
puis la taille de l’image sur le capteur. Commenter les résultats
obtenus et vérifier leur cohérence avec le schéma réalisé.
Grandissement = mesure algébrique OA' / mesure algébrique OA = 6,3 /
(-45) = -0,14.
Taille de l'image renversée : 16 x0,14 ~2,24 cm.
1.2.2.Quel(s)
type(s) de capteur(s) le photographe a-t-il pu utiliser ? Justifier.
L'image de l'oiseau mesure 22,4 mm.
APS-C : dimensions 15,8 x 23,6 mm ou Plein format : dimensions 24 x 36
mm.
1.3. Exercer un
regard critique sur les valeurs des distances précisées par le
photographe dans cette situation.
Il est très difficile d'approcher cet oiseau à une distance inférieure
à 1 m. La taille de l'oiseau semble réaliste.
2. Restitution des couleurs.
L’écran d’un appareil photographique numérique permet d’observer la
photographie obtenue.
Les pixels de l’écran sont de trois types selon qu’ils émettent une
lumière rouge (R), une lumière verte (V) ou une lumière bleue (B).
2.1. La couleur du
plumage du ventre de l’oiseau peut être assimilée à du rouge.
2.1.1. Comment
qualifie-t-on la lumière qui éclaire l’oiseau en milieu naturel ?
La lumière blanche est polychromatique.
2.1.2. En utilisant
le vocabulaire scientifique adapté, formuler une hypothèse expliquant
pourquoi le plumage du ventre de l’oiseau apparaît rouge.
Eclairé en lumière blanche, le ventre rouge absorbe la couleur
complémentaire du rouge, c'est à dire le vert.
2.2. Restitution
des couleurs sur l’écran.
2.2.1. Comment
nomme-t-on la synthèse des couleurs en jeu dans la restitution des
couleurs sur l’écran de l’appareil photographique ?
Synthèse additive.
2.2.2.Quel(s)
est(sont) le(s) pixel(s) activé(s) dans la zone de l’image
correspondant :
- au plumage des ailes, de couleur cyan ; pixels bleu et le vert
- à la pointe du bec qui est noire ; aucun pixel n'est activé.
- à la zone du cou qui est blanche. Pixels rouge, bleu et vert.
3. Règle des tiers.
La photo ci-dessous a été prise avec un appareil muni d’un objectif de
distance focale f ’ égale à 50 mm. Elle respecte la règle des tiers,
règle académique permettant de réussir nombre de cadrages. Cette règle
consiste à placer les éléments forts de l’image sur les lignes
horizontales
et verticales placées au tiers de l’image, et aux points d’intersection
entre ces lignes.

Largeur de la main de l’adulte entre l’index et l’annulaire : 8,5 cm.
3.1. À quel
standard de capteur appartient le capteur de l’appareil utilisé ?
Hauteur de l'image : 5 cm ; largeur : 7,9 cm.
Standard de capteur : 15,8 x 23,6.
3.2. Déterminer à
quelle distance des mains l’objectif doit être placé pour que l’image
obtenue respecte la règle des tiers, c’est-à-dire pour que l’image de
la main de l’adulte soit située entre les deux lignes des horizontales
dites « des tiers ».
Sur l'image, largeur de la main entre index et annulaire 1,7 cm.
Valeur absolue du grandissement g
= 1,7 / 8,5 = 0,2.
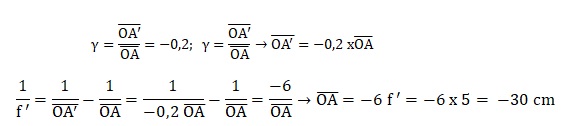
|
L'exploit d'Alan Eustace.
L’étude du saut d’Alan Eustace est conduite dans le référentiel
terrestre. Alan Eustace et son équipement sont modélisés par un point
matériel de masse m. La position d’Alan Eustace est repérée par son
altitude z sur un axe vertical orienté vers le haut, l’origine étant au
sol. Alan Eustace s’est laissé tomber à une date choisie comme origine
des temps (t = 0 s) à partir d’un point A d’altitude zA = 41 148 m par rapport au sol.
1. Énergie potentielle de pesanteur du système.
1.1.Champ de pesanteur au cours de la chute.
1.1.1. Quelle est l’origine de la variation observée entre les valeurs de g et gA ?
g = 9,8 m s-2 au niveau du sol terrestre.
g diminue quand l'altitude augmente : gA = 9,7 m s-2.
1.1.2. Calculer l’écart relatif donné par (g−g A)/g et exprimé en %. Conclure..
(9,8-9,7) / 9,8 ~0,01 ( 1 %).
A 1 % près, on peut considérer g comme constant.
1.2.Travail du poids au cours du saut.
1.2.1. En
considérant que le poids du système {Alan Eustace et son équipement}
est constant, établir l’expression du travail du poids du système lors
du déplacement d’Alan Eustace de A jusqu’au sol en fonction de m, g, et
zA.
Travail moteur du poids en descente ; la descente est verticale jusqu'au sol : W = m g zA.
1.2.2. Calculer la valeur de ce travail.
W = 120 x 9,8 x 41 148 = 4,84 107 J.
1.3.Énergie potentielle de pesanteur.
1.3.1. « Le poids est une force conservative » ; expliquer cette expression.
Une force est conservative lorsque son travail ne dépend pas du chemin suivi mais des positions de départ et d'arrivée.
1.3.2. Définir
l’énergie potentielle de pesanteur Ep du système et montrer que son
expression est Ep = mgz si on choisit une altitude de référence à
préciser.
L'énergie potentielle de pesanteur est choisie nulle au sol.
L'énergie potentielle de pesanteur est égale au travail du poids lors de la chute d'une altitude z au sol. soit m g z.
2. Modélisation de la première phase du mouvement par une chute libre
Alan Eustace atteint un point B, d’altitude zB, après 50 s de chute.
Durant cette phase du mouvement, l’hypothèse est faite que la seule
force s’exerçant sur le système {Alan Eustace et son équipement} est le
poids.
Dans ce cas, on peut montrer que la chute est verticale. Un logiciel de
simulation permet d’obtenir la courbe donnant la valeur de la vitesse v
d’Alan Eustace en fonction du temps t.
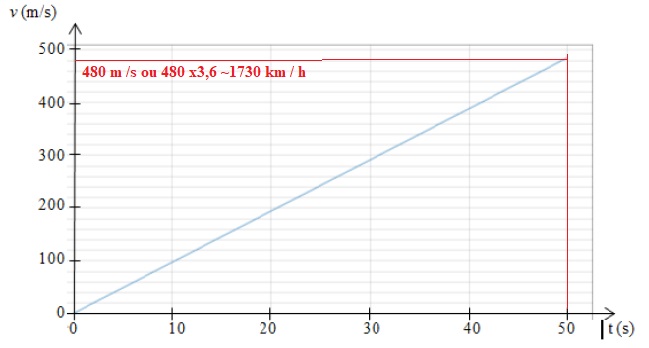
2.1.Montrer que ce
modèle n’est pas compatible avec la donnée du texte introductif
relative à la vitesse maximale atteinte ( 1322 km / h).
2.2. Proposer une hypothèse expliquant l’écart entre valeur calculée et valeur expérimentale.
Il faut prendre en compte les frottements sur les couches d'air.
3. Étude énergétique de la première phase du mouvement
On considère que la chute d’Alan Eustace durant les cinquante premières secondes est verticale.
L’action mécanique exercée par l’air sur Alan Eustace et son équipement
est modélisée par une force de frottement fluide f supposée constante.
L’altitude zB d’Alan Eustace après 50 s de chute est égale à 30 375 m.
3.1.Calcul de la valeur de la force de frottement fluide f dans le cadre de ce modèle.
3.1.1. Énoncer le théorème de l’énergie cinétique. Calculer la valeur de l’énergie cinétique à la fin de cette première phase.
La variation de l'énergie cinétique d'un système est égale à la somme
des travaux des forces extérieures appliquées au système durant cette
variation.
EcB = ½mv2B avec m = 120 kg et vB = 1322 / 3,6 =367 m /s.
EcB = 0,5 x120 x3672 ~8,1 106 J.
3.1.2. Exploiter ce théorème et montrer que la valeur de la force de frottement est de l’ordre de 4.102 N.
Travail du poids entre A et B : W = mg ( zA-zB) =120 x9,8 x(41 148- 30 375) =1,27 107 J.
Variation de l'énergie cinétique entre A et B : 8,1 106 -0 = travail du poids + travail des frottements.
Travail des frottements : 8,1 106 -1,27 107 = -4,57 106 J.
-4,57 106 = -f AB = - 10773 f ; f ~ 4,2 102 N.
3.1.3. Comparer la valeur obtenue au poids du système et conclure quant à la pertinence du modèle de la chute libre.
Poids du système = m g = 120 x9,8 ~1,2 103 N.
La force de frootement est voisine du tiers du poids du système ; on ne peut pas la négliger.
3.1.4. Discuter également de la pertinence de la modélisation de l’action de l’air par une force de frottement constante.
Aux grandes vitesses la valeur de la force de frottement fluide est proportionnelle à la vitesse, voir au carré de la vitesse.
3.2.L’extrait de
programme donné ci-dessous et rédigé en langage Python, permet de
visualiser les énergies cinétique, potentielle et mécanique du système
{Alan Eustace +
son équipement} durant la première phase du mouvement.

3.2.1. À quelle
ligne peut-on lire le choix de l’origine de l’axe vertical ici utilisée
? À quelle position d’Alan Eustace correspond cette origine ?
Ligne 7 : z0 = 0.
Position d'Alan Eustace z0 =0 à t = 0.
3.2.2. En déduire que l’ordonnée d’Alan Eustace au cours du saut est négative pour ce choix d’origine.
L'axe vertical étant orienté vers le haut et son origine prise à la
position initiale d'Alan Eustace, l'ordonnée du sauteur sera négative
au cours de la chute.
3.2.3. Montrer que
l’expression donnée à la ligne 36 est cohérente avec le commentaire de
la ligne 37. Comment varie l’énergie potentielle de pesanteur au cours
du saut ? Quel est son signe ?
L'origine de l'énergie potentielle est prise à la position initiale du sauteur.
A une date t1: Epp1 = mgz1 ; à une date t2 > t1, Epp2 = mgz2.
Epp2 - Epp1 = mgz2 -mgz1 =mg ( z2-z1).
z2-z1 est positif et croît, la variation d'énergie potentielle est positive.
Epp2 > Epp1 .
|
|
|